
Содержание
О магических квадратах
Магических квадратов множество. Многие из них просто завораживают заложенными в них математическими закономерностями, некоторые являются эффективными инструментами для использования на финансовых рынках, а есть и такие, которые являются инструментом для предсказания будущего.
Магическая головоломка в виде квадрата с числами
Нет, пожалуй, ничего необычного в том, что множество великих открытий в математике совершено при решении головоломок. Она из старейших головоломок – волшебный или магический квадрат – первые упоминания о котором есть в китайском труде. Сказать спасибо за эту головоломку мы должны одну очень сведущую в математике речную черепаху.
Математическая черепаха
В соответствии с китайским трактатом III в. до н. э. «Математика в 9 книгах», первый волшебный квадрат подарила человечеству речная черепаха – образ этого магического квадрата было найдено на панцире черепахи (датируется оно 2200 г. до н. э.) . Так именуемый квадрат Ло Шу («речной свиток» в транслировании с древнекитайского) представляет собой квадратную таблицу из 9 полей размером 3 на 3 поля, в каждом из которых числа от одного до девяти.

Как и во всех волшебных квадратах, числа не повторяются, и сумма чисел во всех последовательностях, столбцах и двух диагоналях, проходящих через центр квадрата, однообразна – это и есть ни что иное как «волшебная константа». Ло Шу – обычный или нормальный волшебный квадрат третьего порядка, в нем употребляется тридцать два числа. Волшебный квадрат первого порядка тривиален – он складывается из одного числа. А волшебных квадратов второго порядка не существует. Квадратов более большого порядка нескончаемое множество, где площадь порядка n заполняется числами от одного до n 2 . Волшебная константа (сумма чисел в рядах, диагоналях и столбцах) таких квадратов вычисляется по формуле n(n 2 +1)/2.

Волшебный квадрат 4-го порядка на картине Альбрехта Дюрера «Меланхолия», созданной в 1514 г. Так живописец демонстрировал собственные способности в математике.
Магические квадраты для финансовых рынков
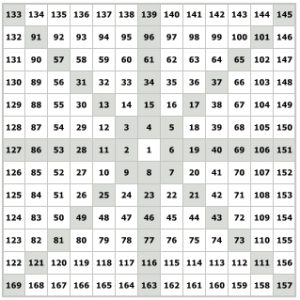
Квдрат девяти (Квадрат Ганна)
В 1920 году Ганном был создан квадрат девяти (Квадрат Ганна). Это своего рода финансовый калькулятор для исследований и торговли. Квдрат девяти Ганн называл шаблонным калькулятором цены и времени. Квдрат девяти бессомненно является одним из самых популярных и таинственных инструментов финансовых рынков.
Квадрат для предсказания будущего
Квадрат Пифагора
Пифагор и его последователи сократили все числа до цифр от одного до девяти включительно, поскольку они являются исходными. Из этих простых начальных цифр (от 1 до 9) могут быть получены все другие числа (двузначные, трехзначные, многозначные). Все жизненные обстоятельства и события в Пифагоровой нумерологии вписываются в числовой ряд от 1 до 9.
Каждый следующий цикл неизменно начинается с 1 и заканчивается на 9. Пифагор пытался придать каждому числу форму геометрической фигуры. Для этого он создал фигурные числа. Особое место отводилось «квадратным» числам. Именно таким числом было 9, которое можно изобразить в виде квадрата.
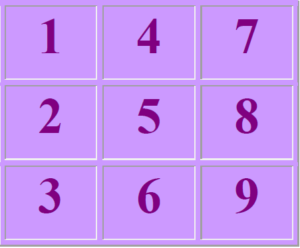
Квадрат Пифагора представляет собой 9 клеток (три по вертикали и три по горизонтали).
Такой квадрат обозначается: «квадрат 3х3». Это означает, что он содержит три столбца и три строки.
Каждая клетка квадрата имеет свое предназначение: внутри квадрата за каждой цифрой закреплено свое место (своя клеточка, своя ячейка), в частности:
- единицы всегда располагаются в верхнем левом углу квадрата (левой верхней клетке);
- пятерки – в середине квадрата (в центральной клетке);
- девятки – в нижнем правом углу квадрата (нижней правой клетке)
- и т.д.
 Этот квадрат имеет несколько названий:
Этот квадрат имеет несколько названий:
«Квадрат Пифагора»,
«магический квадрат»,
«матрица»,
«Числовая матрица»,
«Матрица Пифагора»,
«Числовая матрица Пифагора»,
«Психоматрица»,
«клетки судьбы»,
«9 клеток судьбы»,
«матрица сущности человека» и т.д.
