Содержание
- Квадрат Ганна или Квадрат девяти и его тайны
- Руководство по устройству Квадрата девяти
- Шаблонный калькулятор цены и времени
- Происхождение Квадрата девяти
- Из чего состоит Квадрат Ганна
- Часовая разметка Квадрата Ганна
- Свойства Квадрата Ганна
- Нумерология в основе Квадрата Ганна
- Несколько алгоритмов использования девяти
- Алгоритм расположения чисел в Квадрате Ганна
- Формула для подсчета количества ячеек в циклах
- Ряд с квадратами чётных чисел
- Срединные числа
- Прогресс движения чисел в Квадрате Ганна
- Диагональный и координальный кресты на Квадрате Ганна
- Угол 45 градусов в циклах Квадрата Ганна
- Как определять точные углы для цены при помощи Квадрата 9 Ганна
- Точка отсчета углов для цены
- Как найти информацию по цене и времени смещенную на угол в прошлое или будущее
- Проверяем эту формулу на практике.
- Квадрат девяти Ганна. Итоги
Квадрат Ганна или Квадрат девяти и его тайны
Тайны, которые содержит Квадрат девяти будоражат умы трейдеров вот уже сто лет. Для того чтобы их познать, необходимо постичь все особенности числовых последовательностей в этом удивительном и мистическом инструменте для прогнозов и предсказаний.
Числа – это ключи к зашифрованным знаниям об устройстве вселенной.
Уильям Делберт Ганн.
Во все времена люди пытались предсказывать будущее. Предсказания были буквально обо всём, что нас окружает в этом мире. Финансовые и фондовые рынки не исключение. Одним из гениальных предсказателей первой половины XX века в этой сфере был Уильям Делберт Ганн, который смог создать математический инструмент под названием Квадрат Ганна.
Руководство по устройству Квадрата девяти
Данное руководство включает подробное устройство квадрата Ганна, его свойства, а также некоторые способы применения для определения углов и прогноза цен в прошлом и будущем.
Шаблонный калькулятор цены и времени
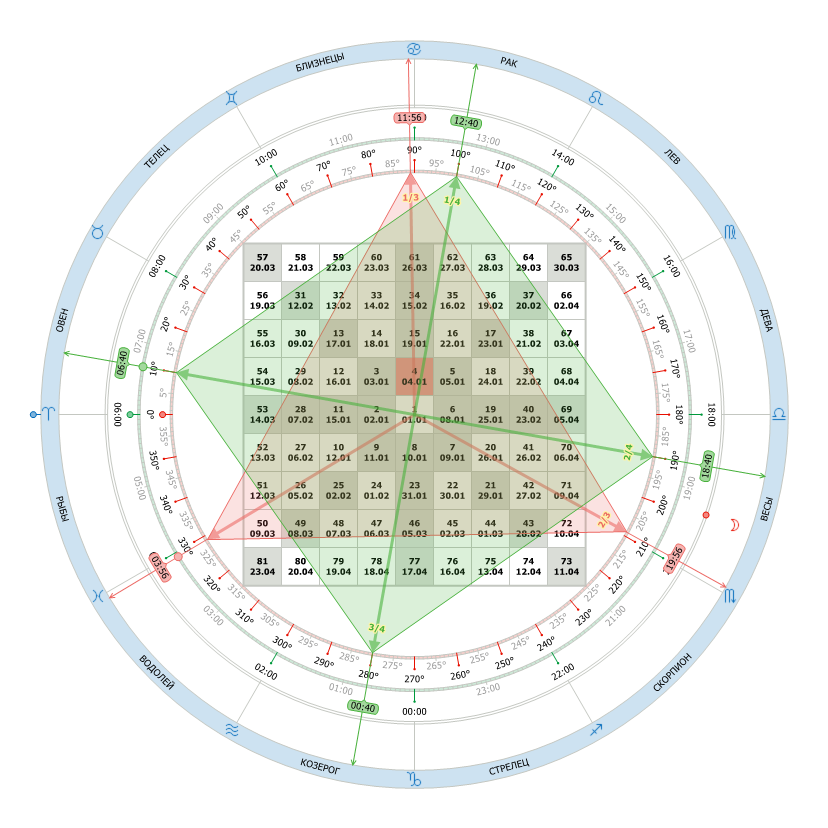
В 1920 году Ганном был создан квадрат девяти (Квадрат Ганна). Это своего рода финансовый калькулятор для исследований и торговли. Квдрат девяти Ганн называл шаблонным калькулятором цены и времени. Квдрат девяти бессомненно является одним из самых популярных и таинственных инструментов рынка. Есть в нём нечто такое, что заинтриговывает абсолютно всех, кто с ним хоть раз сталкивался. Будь то профессионал или начинающий трейдер.
Про методы использования квадрата 9 Ганна написано много всевозможных статей и материалов. Но практически не в одной из этих работ не дано полного объяснения по работе с этим уникадьным инструментом. Каждый кто пытался изучать квадрат 9-ти наверняка задавался вопросом: Что это ? Просто обещание больших заработков для тех кто поймёт секретный код, заложенный в калькуляторе легендарного трейдера? Или это намного больше нежели просто калькулятор – нечто, что откроет путь великого познания окружающей нас действительности, включая финансовые рынки.
Квадрат Ганна (квадрат девяти) – математический финансовый и астрономический инструмент для числовых прогнозов. Шаблонный калькулятор цены и времени, применявшийся величайшим трейдером и великим математиком Уильямом Делбертом Ганном.
Во время знакомства с Квадратом 9-ти, начинаешь понимать, что его использование простирается далеко вне того, что бы быть просто интересным торговым инструментом легендарного предсказателя. Который можно использовать не только в качестве математического, но и что не мало важно, в качестве астрономического калькулятора предсказывающего будущее.
Происхождение Квадрата девяти
Истинное происхождение Квадрата девяти неизвестно. Есть лишь предположение как Ганн его создавал.
Ганн много путешествовал по различным странам, изучая работы древних мудрецов. Его интересовало абсолютно всё, что было связано с предсказаниями и астрологией. Всё что было связано с управлением не только финансовыми рынками, но и всеми мировыми процессами. Во время одной из таких поездок, скорее всего в Египет, он обнаружил нечто очень ценное для себя и похожее на то, что позже им было с успехом использовано при создании Квадрата 9-ти.
Из чего состоит Квадрат Ганна
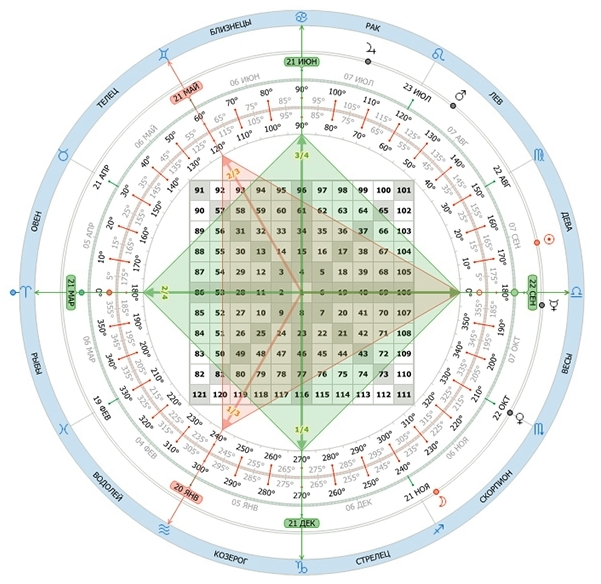
Базовый Квадрат Ганна имеет два набора чисел. Первый набор расположен на окружности, находящейся снаружи квадрата.
Второй набор находится на плоскости квадрата.
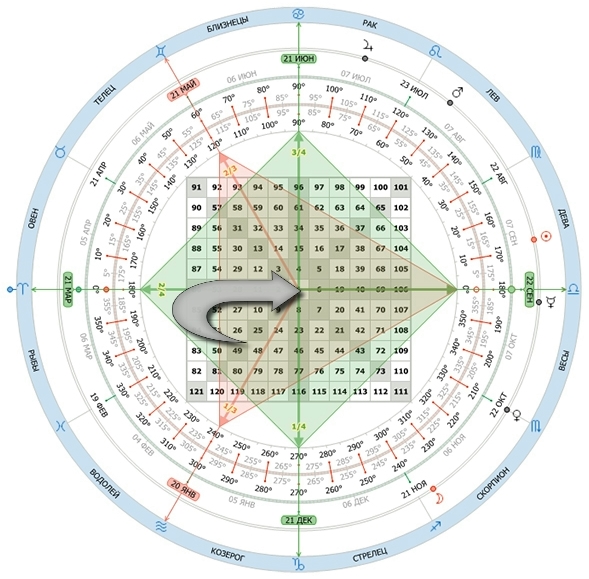
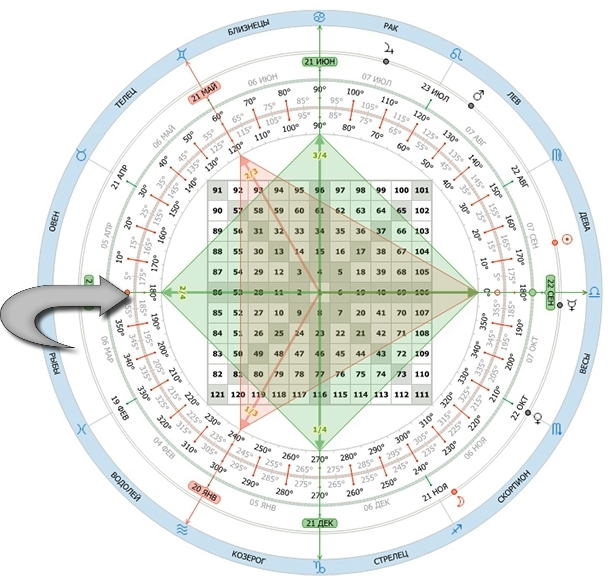
Ганн разделил окружность на градусы. Кроме того он добавлял на окружность дни года и 24 часа дня.
Весеннее равноденствие – 21 марта, совпадает с отметкой 0 градусов, когда солнце находится в овне. Этот день называют первым днём весны и началом естественного года.
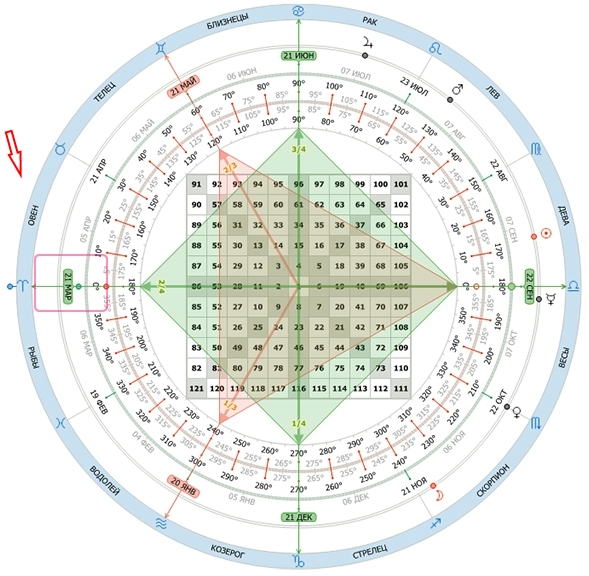
Летнее солнцестояние – 21 июня совпадает с отметкой 0 градусов, когда солнце находится в раке. Этот день называют самым долгим днём года для северного полушария.
Осеннее равноденствие – 22 сентября совпадает с отметкой 0 градусов, когда солнце находится в весах. С этой даты начинается сезон падений и солнце буквально начинает падать внизу экватора Земли.
И наконец зимнее солнцестояние – 21 декабря совпадает с отметкой 0 градусов, когда солнце находится в козероге. Это самый короткий день года в северном полушарии отмечающийся зоной зимы.
Данная разметка показывает нам, что даты не делят круг на равные части. От весеннего равноденствия до летнего солнцестояния промежуток составляет 92 дня. От летнего солнцестояния до осеннего равноденствия – 93 дня. От осеннего равноденствия до зимнего солнцестояния – 90 дней. И наконец от зимнего солнцестояния до осеннего равноденствия – также 90 дней. В сумме это составляет ровно 365 дней.
Часовая разметка Квадрата Ганна
Когда Ганн применял деление на 24 часа он размещал 6:00 часов на отметке 0 градусов, как слева так и справа, напротив середины стороны квадрата. Делал он это не случайно. Дело в том, что в дни равноденствия – 21 марта и 22 сентября солнце встаёт и садится именно в 6:00 часов.
Земля поворачивается на один градус каждые четыре минуты, поэтому 24 часа делят круг ровно на 360 четырёхминутных промежутков.
Свойства Квадрата Ганна
Ганн в работе использовал квадраты, которые имели начало градусного отсчёта по центру как справа так и слева, а также с левой нижней стороны диагонали образующей квадраты нечетных чисел. Направление шкалы он использовал как по часовой стрелке, так и против часовой. И наконец, что касается чисел на плоскости квадрата.
Изучение личных работ Ганна показало, что он использовал квадраты в которых числа на плоскости были расположены также как и числа на окружности. Т.е. как против так и по часовой стрелке. Неважно какое направлении в расположении чисел используют, так как результаты от этого не сильно изменяются.
Нумерология в основе Квадрата Ганна
Мир построен силою чисел.
Уильям Ганн большое значение придавал нумерологии. Особенно числам упоминаемым в Библии. Это натолкнуло его на мысль о том, что в них заложен некий символизм. Числа – это ключи к зашифрованным знаниям об устройстве вселенной. Так число семь, неоднократно упоминающееся в Библии – семь ангелов, семь дней творения, и такое же число нот в октаве, подсказало идею Ганну в том, что семёрка символизирует как время так и ритм. Важным числом для Ганна было также число 3,5 и не только потому, что оно является половиной семи, но и из-за особой роли отводимой ему в Библии. Христос – дитя, был спрятан в Египте на 3,5 года. Его служение людям продолжалось ровно 3,5 года. Видение Даниила – 42 месяца или 3,5 года.
Либо число двеннадцать, которое у Ганна символизируется с космосом. 12 знаков зодиака и так далее.
Используя эти числа он составлял таблицу магических квадратов с которыми часто сверялся при изменении рыночных цен. Изучая труды великих мудрецов прошлого Ганн не обошел своим вниманием Пифагора, который говорил, что мир построен силою чисел, а это значит, что числа должны быть ключом к пониманию мира. Весьма много предсказаний были и могут быть сделаны именно с помощью чисел. Создание квадрата девяти лишний раз доказывает тот факт, что у Ганна было особое отношение к числам и циклам и всему, что с ними связано.
Ганн не оставил инструкций относительно того как использовать Квадрат девяти. Изучать этот уникальный торговый инструмент каждому из нас приходится самостоятельно. Поэтому в сети интернет можно встретить множество различных версий по его использованию. Ганн говорил, что именно девять чисел мы используем в измерении всего и мы не можем выйти вне этих девяти цифр, не начав повторяться и использовать вновь. Если мы поделим 360 на 9, то получаем 40, что измеряет 40 градусов, 40 месячцев, 40 дней или 40 недель. Это показывает, что основания и вершины биржевых котировок часто выходят в этих углах, измеренных как 1/9 полного круга.
Несколько алгоритмов использования девяти
1. Если добавить девять к любому числу, результат всегда можно уменьшить до начального числа через сложение цифр получившихся в числе.
Например:
1+9=10 1+0=1
Сумма цифр числа десять равна единице.
2+9=11 1+1=2
Сумма цифр числа одиннадцать равна двум.
И так далее:
3+9=12 1+2=3
5+9=14 1+4=5
2. Если умножить любое число на 9, то результат можно уменьшить до 9 через сложение цифр получившихся в числе.
Например:
9 умножить на 5, равно 45. Сумма цифр в числе 45 равна девяти.
9х5=45 4+5=9
И так далее:
9x8=72 7+2=9
9x22=198 1+9+8=18 1+8=9
2. Сумма цифр от 1 до 9 равно 45. Сумма цифр 45, опять таки даст нам результат – девять.
1+2+3+4+5+6+7+8+9=45 4+5=9
Алгоритм расположения чисел в Квадрате Ганна
Число девять для Ганна имело своего рода фундаментальное значение. И являлось основопологающим в большинстве его вычислений. На квадрате девяти нет ничего лишнего. И все числа в его ячейках расположены не просто так. В их расположении заложен специальный алгоритм. Благодаря которому можно производить вполне реальные вычисления, согласно результатов которых у нас появляется возможность делать довольно точные прогнозы на будущее.
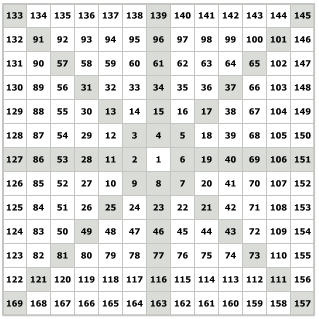
Квадрат Ганна или Квадрат девяти является спиралью чисел, начинающейся с ячейки под номером 1. Раскручиваться спираль начинает с ячейки под номером 2, размещённой слева от центра. Остальная часть спирали чисел вокруг центра по часовой стрелке движется к ячейке с номером девять.
Двигаясь от ячейки с номером 2 до ячейки с номером 9, мы совершим одно 360-градусное движение. Ганн называл такое движение – “квадрат” или “цикл”. Квадрат девяти получил своё название из-за того, что первый полный оборот оканчивается на числе девять. На ячейке с номером девять заканчивается первый цикл чисел вокруг центра.
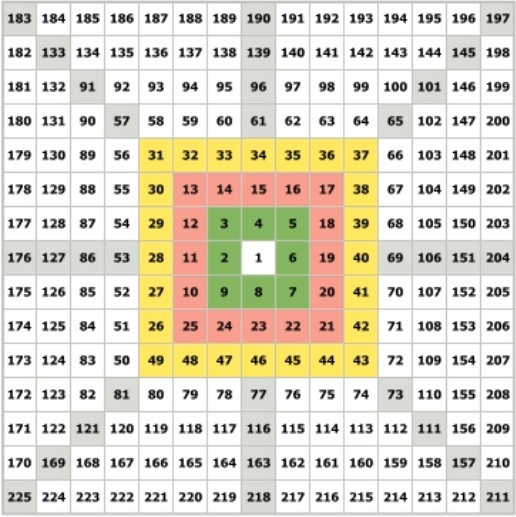
Двигаясь от ячейки 9 до ячейки 25, мы совершим ещё одно 360-градусное движение. Следовательно на ячейке с номером 25 заканчивается второй цикл вокруг центра Квадрата девяти. Чтобы стало понятно о чём идёт речь, циклы в Квадрате Ганна выделены разными цветами.
Ганн идентифицировал циклы по самому большому числу в одном обороте. Это всегда число которое завершает 360-градусное движение. Так в примере движение от 10 к 25 идентифицируется как оборот заканчивающийся на 25 или “оборот двадцати пяти”.
Если присмотреться к числам ячеек, на которые заканчиваются циклы, а это 9, 25, 49, 81, 121, 169 и т.д., то можно увидеть, что это ничто иное как квадраты нечетных чисел. А именно квадрат трёх, семи, пяти, девяти и т.д.
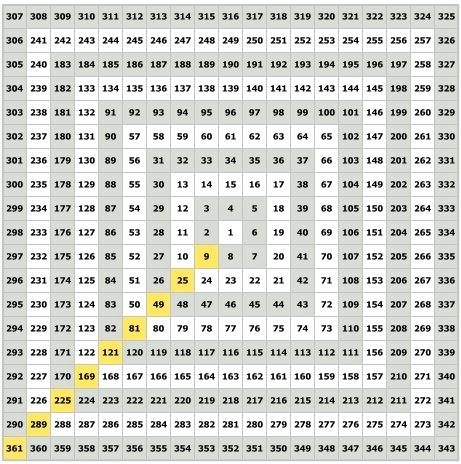
Кстати сказать, Квадрат девяти Ганн также называл “Квадратом нечетных чисел”.
Итак мы знаем как идентифицировать циклы, и что каждый цикл заканчивается на ячейке с числом равным квадрату нечетного числа. Которое всегда располагается в левом нижнем углу каждого цикла. Каждый цикл в квадрате девяти содержит на восемь чисел больше чем предыдущий. Первый цикл – от двух до девяти содержит 8 цифр. Второй оборот состоит из шестнадцати чисел. 8+8=16. Третий оборот состоит из 24 чисел. 16+8=24 и т.д.

Формула для подсчета количества ячеек в циклах
Если нам требуется узнать количество ячеек, в том или ином цикле, пересчитывать их в ручную не всегда удобно, так как циклы могут быть достаточно большими. Есть формула для подсчета количества ячеек в каждом цикле.
Например, нам нужно найти количество ячеек в цикле 225. Для этого в начале
-Находим нечётный квадрат, заканчивающий цикл, в нашем случае – 225;
-Вычисляем квадратный корень из 225, он равен 15;
-15 делим на 2, получаем 7,5;
-Вычитаем 0,5 из этого числа, получаем 7;
-Умножаем 7 на 8, получаем 56.
Таким образом цикл, оканчивающийся на числе 225 содержит 56 ячеек.
Если же нам требуется знать количество яччеек, находящихся в основании квадрата цикла. Для этого достаточно получить квадратный корень из нечетного квадрата заканчивающего цикл. К примеру в том же цикле 225, основание квадрата будет содержать 15 ячеек.
Ряд с квадратами чётных чисел
Ганн говорил, что всё в нашем мире стремится к гармонии. Если на квадрате девяти есть ряд квадратов нечетных чисел, значит должен быть аналогичный ряд, но только с квадратами чётных чисел. И такой ряд действительно есть. Начинается он с ячейки с номером 4.
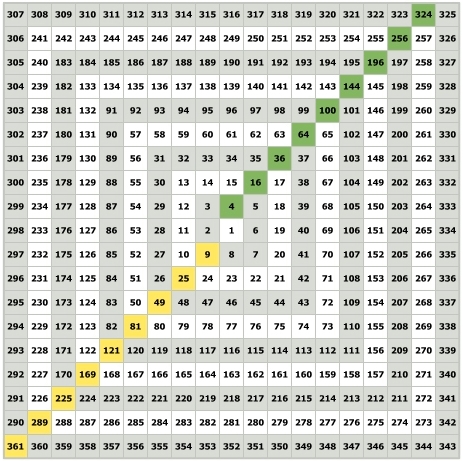
Обратите внимание – 4, 16, 36, 64, 100, 144 и т.д. Всё это квадраты четных чисел.- 2, 4, 6, 8. И есть множество интересных фактов относящихся к квадратам четных чисел.
Число четыре делит квадраты четных чисел без остатка.
Например, 144 – это чётное число и 144 делённое на 4 даёт в результате 36. Когда квадрат чётного числа делится на четыре без остатка, получившееся число будет также квадратом чётного числа.
Другими словами 1/4 любого чётного квадрата также является чётным квадратом.
Например, 12 х 12 = 144 или квадрат числа 12. 144 разделить на 4 равно 36. 36 равняется квадратом 6.
Сравнив расположение чётных и нечетных чисел на квадрате девяти, мы увидим, что они противоположны друг другу.
Ганн сказал:
Мы используем квадрат чётных и нечётных чисел, чтобы получить не только доказательства движения рынка, но и его причины…
Срединные числа
Помимо рядов составляющих квадраты чётных и нечётных чисел, Квадрат девяти включает в себя ряды составляющие числа половины между этими квадратами. Числа на таких рядах называются срединными числами.
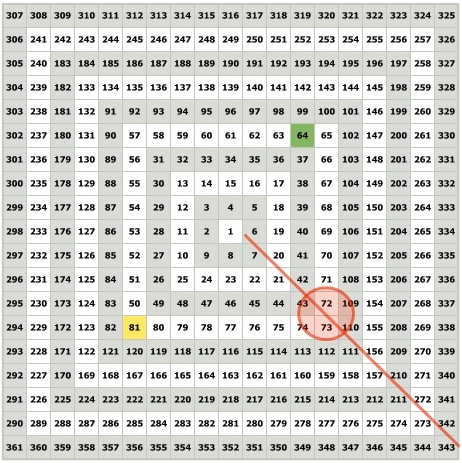
На Квадрате девяти, числа образующие половину между квадратом чётного числа и квадратом большего нечётного числа, расположены в направлении правого нижнего угла.
Например, срединное число между 64 и 81 – квадраты 8 и 9 соответственно, равно 72,5. Линия показывающая расположение срединных чисел, направлена в нижний правый угол.
Срединные числа между квадратом нечётного числа и квадратом большего чётного числа, расположены в направлении левого верхнего угла.
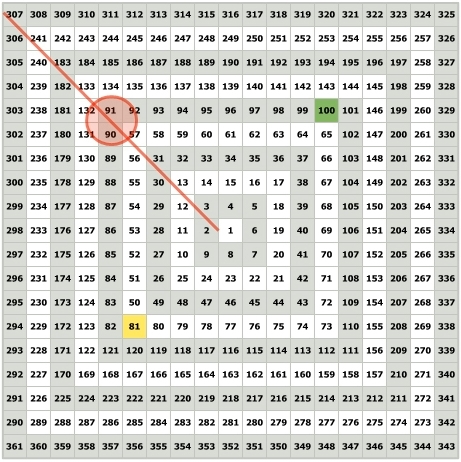
Срединное число между 81 и 100 равно 90,5.
Прогресс движения чисел в Квадрате Ганна
Следуя Квадрату девяти, прогресс движения к квадрату нечётного числа к квадрату чётного числа или наоборот даёт нам сначала числа равные 1/4 квадрата, а затем срединные числа – 1/2 квадрата, потом числа равные 3/4 квадрата. Числа равные 1/4 расположены на правой и на левой горизонтальных осях квадрата.
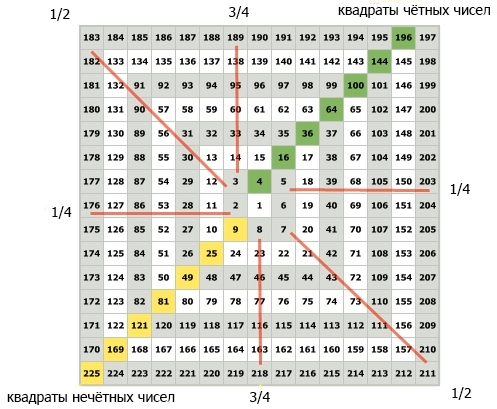
Например, между чётным квадратом 196 и нечетным 225 первое четвертичное число равно 203,25. Числа равные 3/4 квадрата расположены на верхней и нижней вертикальных осях.
Например, 3/4 между нечетным квадратом 169 и чётным 196 равно 189 и 25.
Числа равные 1/4 и 3/4 квадрата не являются целыми числами. Числа подобные 203,25 не отображаются на квадрате. Они находятся между целыми числами, составляющими Квадрат девяти. На этом же примере представлен такой же квадрат, но теперь эти точки используются, чтобы разделить полный оборот на 8 частей.
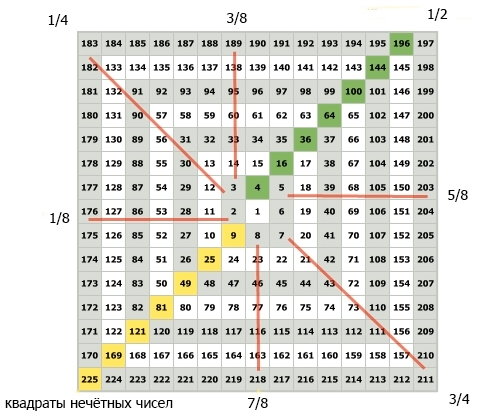
В данном случае мы получаем числа равные 1/8 квадрата.
Диагональный и координальный кресты на Квадрате Ганна
На Квадрате девяти Ганн выделил два креста назвав их диагональным и координальным крестами.
Диагональный крест выглядит как буква Y, а координальный как знак плюс “+”. И это было не случайно, так как одно из правил которое Ганн применял для использования Квадрата девяти гласит:
Числа принадлежащие диагональному и координальному крестам, имеют важное значение для анализа.
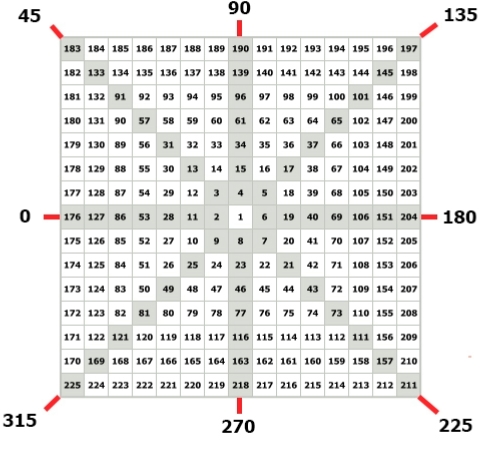
Применяя Квадрат девяти Ганн чертил прямые линии от центра квадрата к кругу на который были нанесены градусы. Ганн называл их углами. Их величина определялась градусами которые они касаличсь на круге. Числа на координальном кресте называют координальными числами. Эти числа все отделены приращениями 90 градусов, т.е. 90, 180, 270 и 360, которые возвращают Вас в место положения с которого Вы начинали движение. Числа на диагональном кресте, которые соединяют четыре угла квадратной основы, т.е. числа углов, также отделены приращениями в 90 градусов.
Координальный и диагональный кресты делят Квадрат Ганна на восемь равных частей через каждые 45 градусов. Это не просто случайность, так как углы 45 градусов также имеют большое значение при работе с Квадратом девяти.
Угол 45 градусов в циклах Квадрата Ганна
Обратите Ваше внимание на одну небольшую особенность, она нам пригодится при некоторых вычислениях.
В первом цикле вокруг центра есть одна цифра, отделяющая каждые 45 градусов, именнок каждые из восьми цифр составляющих первый цикл. Во втором цикле от 10 до 25 присутствует уже две цифры отделяющие каждый угол 45 градусов. Это числа 10 и 11, 12 и 13, 14 и 15 и т. д. В цикле номер три 26-49 есть уже 3 цифры. В цикле под номером 1000 было бы тысяча циклов или ячеек отделяющих каждые 45 градусов.
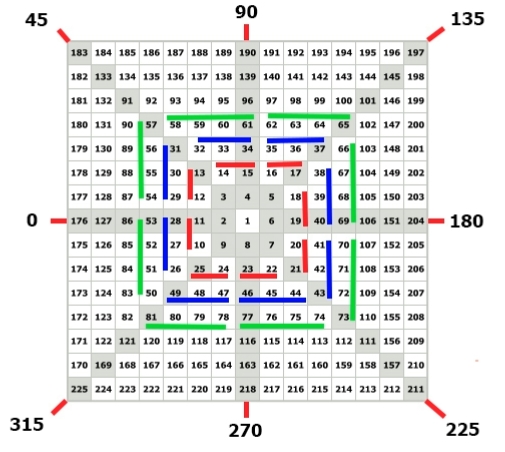
Это важно запомнить, так как данная закономерность используется при вычислении точного угла на котором располагается цена по тому или иному финансовому инструменту на Квадрате девяти. Для чего нам нужно значение точного угла для цены и как его можно использовать в вычислениях будет рассказано в следующих статьях по использованию Квадрата Ганна – Уроки по практическому применению различных методов прогнозирования с использованием Квадрата 9 Ганна.
Как определять точные углы для цены при помощи Квадрата 9 Ганна
Допустим по какому либо вымышленному финансовому инструменту цена равна 14,30$.
Первое, что нам нужно сделать это привести цену к формату чисел не использующих запятую – 14,30$ = 143

В данном примере мы переносим запятую на один знак вправо. В итоге получаем число 143.
Отмечаем ячейку с числом 143 на Квадрате 9 Ганна.
Следующий шаг который мы должны сделать, это определить ячейку на диагональном или координальном крестах с числом наиболее близко раположенном к искомому. В данном случае искомое число 145, которое расположено в ячейке на диагональном кресте.

Теперь нам нужно определить цикл в котором находится данная ячейка. Ячейка с числом 143 находится в 6 цикле.

Это как мы уже знаем означает то, что в данном цикле есть по 6 цифр между каждыми 45 градусами.
Теперь вычисляем размер на который увеличивается число при перемещении на один градус. В дальнейшем будем называть такое перемещение – одноградусной фракцией цикла. Для этого разделим количество ячеек между углами на 45 градусов. 6 делим на 45 и получаем количество одноградусной фракции используемой для этого цикла.
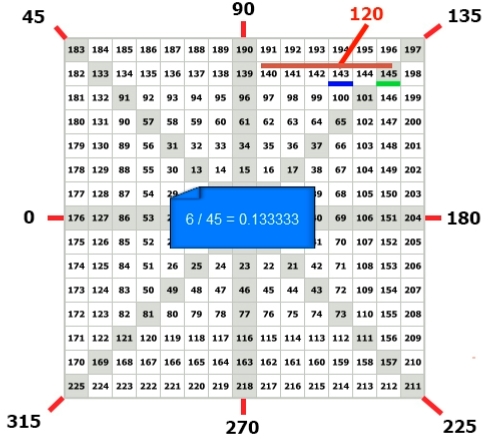
Теперь считаем разницу между нашим искомым числом и числом 145 – она равна двум.

Разделим полученный результат на одноградусную фракцию нашего цикла.

Получаем 15 градусов.
Теперь прибавляем это количество градусов к 45, либо отнимаем от 135, в зависимости от того какую точку мы используем для начала отсчёта, то есть слева или справа от оси.
 Так как ближайшее число находится именно на этом градусе, 45+15 получается 60. 135-15 получается 120. Точный угол для цены 14,30$ либо 60, либо 120 градусам. Так как вычислять такие углы мы будем часто, а цены могут иметь больше цифр, чем в приведённом нами примере после перемещения запятой. К примеру для пары EUR/USD цена может составлять и пять и шесть цифр, а увеличивать Квадрат девяти не всегда удобно. Предлагаем заранее подготовить расчеты и записать их в отдельную таблицу. А при необходимости просто использовать готовые данные.
Так как ближайшее число находится именно на этом градусе, 45+15 получается 60. 135-15 получается 120. Точный угол для цены 14,30$ либо 60, либо 120 градусам. Так как вычислять такие углы мы будем часто, а цены могут иметь больше цифр, чем в приведённом нами примере после перемещения запятой. К примеру для пары EUR/USD цена может составлять и пять и шесть цифр, а увеличивать Квадрат девяти не всегда удобно. Предлагаем заранее подготовить расчеты и записать их в отдельную таблицу. А при необходимости просто использовать готовые данные.
Точка отсчета углов для цены
Как уже было сказано ранее, нет большой разницы какую из трёх предлагаемых Ганном точек для начала отсчета градусов на окружности использовать. Поэтому для будущих своих вычислений определитесь с какой-нибудь одной и постоянно используйте её, чтобы не происходило разного рода путаниц с числовыми обозначениями углов.
Как найти информацию по цене и времени смещенную на угол в прошлое или будущее
В расчетах прогноза с помощью инструмента Квадрат девяти часто необходимо знать информацию по цене или времени смещенную на конкретно взятый угол в прошлое или будущее. К примеру, у нас есть цена 13,90$. Нас интересует цена которая будет одним циклом выше или ниже её. Берём ячейку с числом 139, она находится на вертикальной оси координального креста на угле 90 градусов.
 К квадратному корню искомого числа прибавляем 2, после чего результат возводим в квадрат. Если требуется найти число которое находится на том же угле, что и исходное, но на один цикл выше.
К квадратному корню искомого числа прибавляем 2, после чего результат возводим в квадрат. Если требуется найти число которое находится на том же угле, что и исходное, но на один цикл выше.
 Если требуется найти число которое находится на том же угле, что и исходное, но на один цикл ниже искомого. К квадратному корню искомого числа не прибавляют 2, а отнимают. После чего результат опять возводят в квадрат.
Если требуется найти число которое находится на том же угле, что и исходное, но на один цикл ниже искомого. К квадратному корню искомого числа не прибавляют 2, а отнимают. После чего результат опять возводят в квадрат.
Проверяем эту формулу на практике.
Вычисляем квадратный корень из 139. Прибавляем или отнимаем 2 к полученному результату. Далее возводим результаты в квадрат.
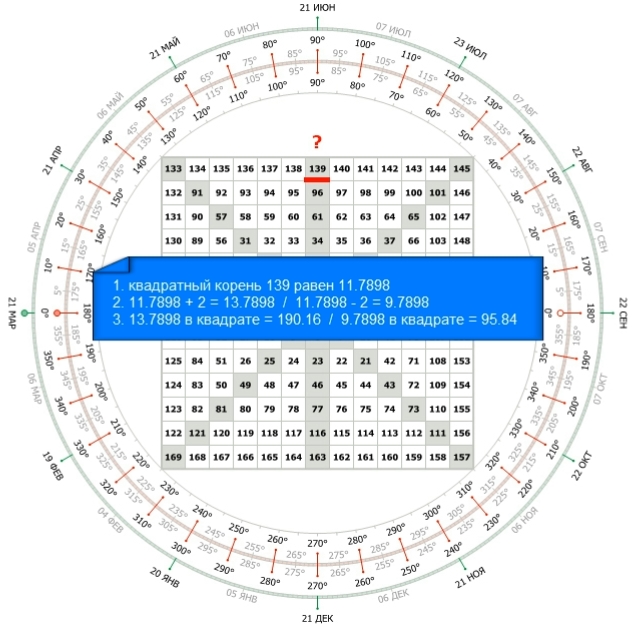 Мы получаем числа 190,16 и 95,84.
Мы получаем числа 190,16 и 95,84.
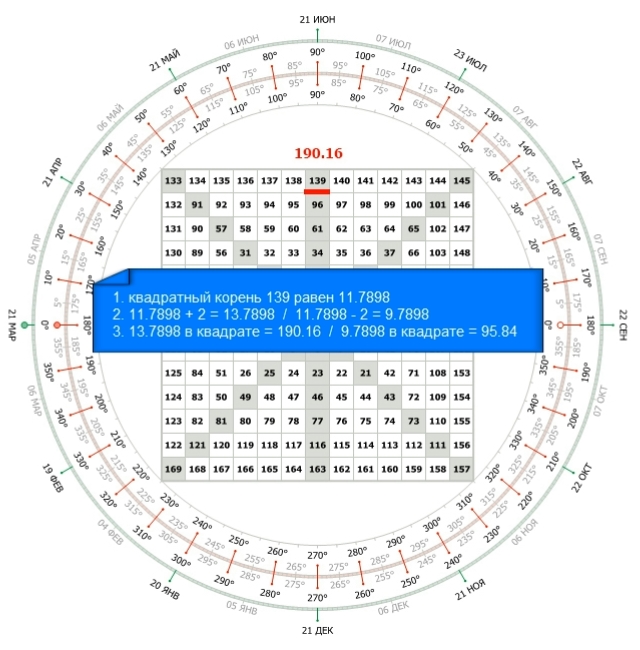 Это числа которые расположены на один цикл выше и ниже искомого числа. Переносим запятую на один знак влево, получаем цену 19,2$ и 9,58$. Большинство перемещений по плоскости квадрата не заканчиваются целым числом, как в данном примере. Только если мы начнём перемещение с нечётного квадрата, например, с 81 или 121 и т.д. мы получим целое число в результате.
Это числа которые расположены на один цикл выше и ниже искомого числа. Переносим запятую на один знак влево, получаем цену 19,2$ и 9,58$. Большинство перемещений по плоскости квадрата не заканчиваются целым числом, как в данном примере. Только если мы начнём перемещение с нечётного квадрата, например, с 81 или 121 и т.д. мы получим целое число в результате.
Перемещаться по квадрату с помощью этой формулы можно не только на целые циклы т.е. 360 градусов. Перемещения могут быть на 1/2 цикла – т.е. 180 градусов, 1/4 – 90 градусов, 1/8 цикла – 45 градусов. То есть на основные градусные величины о которых говорил Ганн. У данных перемещений используется всё та же формула, только на втором шаге, т.е. когда мы прибавляли или отнимали 2, используем следующие числа:
| +/- 2 | 1 цикл -360 градусов |
| +/- 1 | 1/2 цикла -180 градусов |
| +/- 0,5 | 1/4 цикла -90 градусов |
| +/- 0,25 | 1/8 цикла -45 градусов |
Главное запомнить. Если интересует будущее прибавляем, если прошлое отнимаем.
Квадрат девяти Ганна. Итоги
Данной информации вполне достаточно для того чтобы получить общее представление о том, что из себя представляет Квадрат девяти Ганна. Для тех из Вас кто желает более подробно изучить этот уникальный инструмент, советуем прочитать книгу Патрика Микулы “Пособие по применению Квадрата 9”

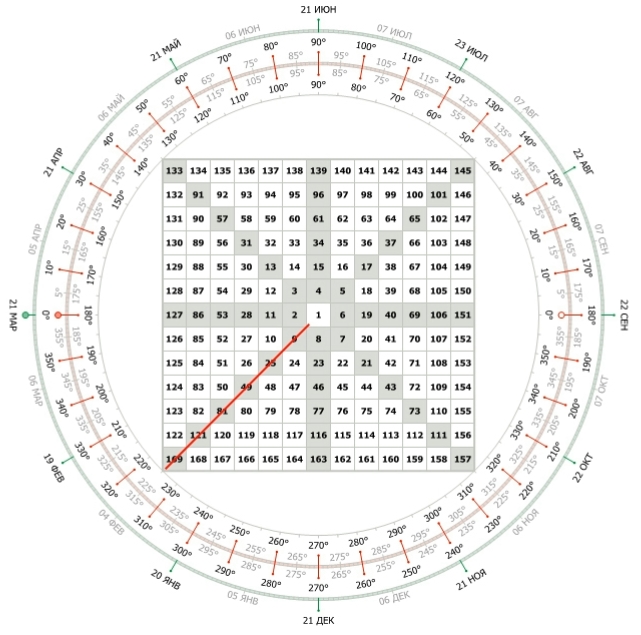

Мне понравилось объяснение формулы и последовательности чисел.
Мне понравилось описание координальных чисел и их углов.