Простые числа

Простые числа для математики – сверкающие драгоценные камни среди нескончаемых песков числительных. Простое число – это число, которое невозможно нацело поделить ни на какое другое, не считая единицы и его самого. Другие целые числа – составные, они складываются из разных комбинаций между собой.

Последовавательность простых чисел

Количество простых чисел имеет бесконечную последовательность, и до сих пор – не обращая внимания на многие миллионы истраченных впустую человеко-часов – никто не отыскал метода угадать их появление в числовой последовательности. В случае, если такая закономерность и существует, мы не можем ее отыскать. Приходится выискивать каждое простое число поштучно. Сама мысль простого числа достаточно несложна, но, разумеется, чтобы доказать, что некое число есть простым, его необходимо последовательно поделить на все без исключение числа, которые должны быть меньше его, дабы убедиться, что в любых ситуациях нацело (без остатка) оно не делится. Это упражнение в полной мере подходит для тех нескольких простых чисел, что проходят в школе, но вот числа покрупнее требуется дробить десятки, сотни, кроме того миллиарды раз, перед тем как мы сможем подтвердить, что они являются простыми.

 

Древний метод поиска простых чисел

Сейчас поиск простых чисел ведут с помощью скоростных суперкомпьютеров, но способ перебора чисел-кандидатов, что они применяют, был основан давным-давно. Простые числа также составляют основу для шифрования данных, используемых для обеспечения безопасности в телекоммуникациях, но и нашим предкам были известны способы применения простых чисел. Например известно что простые числа применялись уже 20 000 лет назад для старейшего математического приспособления – кости Ишанго, найденные на территории современного Конго.
В «Началах» Эвклид продемонстрировал, что количество простых чисел безмерно, но это не предотвращает поиск людей для нахождения последнего числа. «Решето Эратосфена» — один из первых способов открытия простых чисел, изобретателем которого считают астронома и древнегреческого математика, жившего в III в. до н. э.

Метод Решета — последовательность подробных наставлений, — позволяющих обнаружить все простые числа в заданном множестве чисел, берущем начало с двойки. Во-первых, нужно исключить все числа, кратные двум, первому простому числу. Это будут все четные числа; оставшиеся простые числа — нечетные. Вторым шагом нужно исключить все числа, кратные трём, далее — пяти (число четыре уже исключено), после этого семи. В случае, если множество чисел, среди которых мы ведем поиск, меньше ста, этих шагов достаточно, дабы найти все 25 простых чисел. С более большими множествами процесс исключения кратных нужно продолжать, опираясь на новые простые числа по мере их появления. Этому методу 2300 лет, но он по прежнему остается лучшим методом поиска небольших простых чисел, до отметки 100 000 000 либо около того.

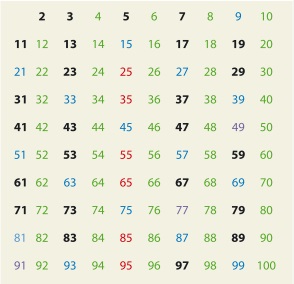
Цветовой код «решета» показывает простые числа меньше ста. Цвета соответствуют множествам чисел, кратных простым от двух и более.
Зелёный – кратные 2
Синий – кратные 3
Красный – кратные 5
Фиолетовый – кратные 7
Чёрный – простые числа.

Маленькая теорема с огромными проблемами

Пьер де Ферма, выдающийся великий математик XVII в., создал собственный инструмент для поиска простых чисел. Самая узнаваемая «шутка» Ферма заключалась в том, что он не повестил мир о доказательстве собственной «последней ( Великой) теоремы». Его малая теорема о простых числах менее известна. В первый раз он писал о собственной малой теореме в письме Бернару Френкилю де Бесси в 1640 г. Ферма сообщал другу, что результатом уравнения a p – a, где p — простое число, а а — любое, постоянно будет число, кратное p. Верный себе, Ферма не привел этого решения, передав де Бесси задачу отыскать его самостоятельно. Но ни де Бесси, ни кому-либо это не удавалось. Ферма унес ответ (если он у него был) с собой в могилу. Потребовалось еще около сотни лет, дабы швейцарский великий математик Леонард Эйлер доказал эту теорему (это подтверждение — одно из многих его блестящих достижений). Малая теорема Ферма употребляется в качестве первого шага в длящемся поиске простых чисел. Сейчас эта теорема формулируется так: a p – 1 = b, в случае, если деление b на p дает в остатке единицу. Значение переменной a произвольно, и в случае, если итог вычислений остается верным, число p примется «возможно простым числом». Но достаточно одного значения b, при котором ответ делается неверным, дабы продемонстрировать, что в данном конкретном случае p — составное число.

Простые числа против хищников

Периодические цикады находятся бóльшую часть собственной жизни в виде бескрылых куколок, насыщающихся соками из скрытых в земле корней деревьев. Для разведения они должны вылезть на поверхность почвы
и трансформироваться в крылатую взрослую особь. Тысячи куколок преобразовываются в бабочек в один момент, воображая красивый пир для любого подстерегающего их хищника. Но превращение цикад происходит один раз в 13 либо 17 лет. Этот выраженный простым числом цикл между поколениями цикад делает неосуществимым для хищников синхронизацию их жизненных циклов с жизненным циклом цикад.