Всё о комплексных числах

Когда математики захотели разделить число на число там, где разделить нацело невозможно, они придумали дроби.
Когда они захотели вычесть большее число из меньшего, они придумали отрицательные числа.
Всякий раз, когда чего-то нельзя сделать, математики придумывают что-нибудь новое, чтобы все-таки сделать это.
Так что, когда невозможность извлечь квадратный корень из отрицательного числа начала серьезно раздражать, они… догадайтесь, что сделали?

И. Стюарт

Понятие комплексного числа

Среди всех множеств чисел, которые изучаются в курсе основной, старшей школы, а также в курсе высшей математики, можно выделить два множества, которые являются самыми широкими множествами. Это действительные и комплексные числа, при этом стоит отметить, что множество комплексных чисел шире, чем множество действительных и включает его. Комплексные числа в математике, которая изучается в школе, рассматриваются крайне редко. В основном это происходит в классах с углубленным изучением математических дисциплин. В курсе высшей математики с комплексными числами знакомятся при изучении такого раздела как алгебра, где впервые встречаются комплексные числа.

Помимо и даже против воли того или другого математика, мнимые числа снова и снова появляются на выкладках, и лишь постепенно, по мере того как обнаруживается польза от их употребления, они получают все более широкое распространение.

Ф. Клейн.

Итак, для того чтоб ответить на вопрос какие числа называются комплексными, введем понятие комплексного числа.

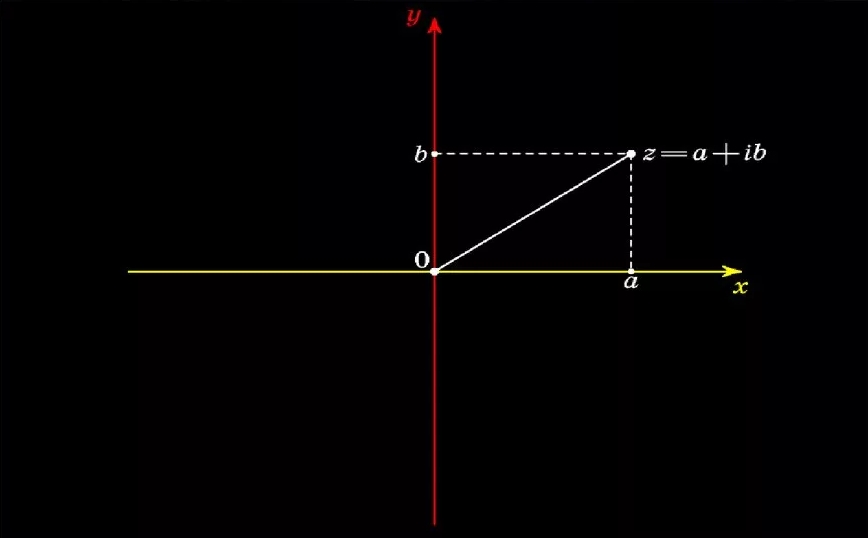
Комплексным числом называется выражение вида a + b * i, где i – мнимая единица – некий символ, квадрат которого равен -1, а числа а и b – это действительные числа. При этом выражения a и b * i, соответственно, это действительная и мнимая часть комплексного числа.

То есть действительная часть комплексного числа – это слагаемое, которое не содержит мнимую единицу, а для того, чтоб найти мнимую часть комплексного числа, достаточно рассмотреть второе слагаемое, содержащее i. Часто мнимые числа содержат в своей записи действительные числа, то есть b * i – это число мнимое, а b – действительное число, которое в нем содержится. Число а – это действительная часть комплексного числа.

Рассмотренная форма записи комплексного числа – это алгебраическая форма комплексного числа. Рядом с ней существуют, так называемые, тригонометрическая и показательная формы записи комплексных чисел. Нельзя сказать какая из них будет более удобная для вычислений, но наиболее распространенными являются алгебраическая и тригонометрическая формы. Им и уделим особое внимание.

Никто ведь не сомневается в точности результатов, получаемых при вычислениях с мнимыми количествами, хотя они представляют собой только алгебраические формы и иероглифы нелепых количеств.

Л. Карно.

Действия над комплексными числами в алгебраической форме

Прежде чем рассматривать другие формы записи комплексного числа рассмотрим не только сами комплексные числа, но и операции над ними.

К операциям над комплексными числами в алгебраической форме относятся:

• Сложение;
• Вычитание;
• Умножение;
• Деление.

Как считать и проводить алгебраические операции, содержащие комплексные числа

Введем комплексные числа как примеры 2 + 3 * i, 1 – 5 * i и рассмотрим выполнение указанных выше операций.

Сложение

2 + 3 * i + 1 – 5 * i = 2 + 1 + 3 * i – 5 * i = 3 + (3 – 5) * i = 3 – 2 * i.

Вычитание

2 + 3 * i – (1 – 5 * i) = 2 – 1 + 3 * i – (-5 * i) = 1 + (3 + 5) * i = 1 + 8 * i.

Умножение

(2 + 3 * i) * (1 – 5 * i) = 2 * 1 + 3 * i * 1 – 2 * 5 * i – 3 * i * 5 * i = 2 + 3 * i – 10 * i + 15 = 17 – 7 * i.

Деление

(2 + 3 * i) / (1 – 5 * i) = (2 + 3 * i) * (1 + 5 * i) / ((1 – 5 * i) * (1 + 5 * i)) =

= (2 * 1 + 3 * i * 1 + 2 * 5 * i + 3 * i * 5 * i) / (1 * 1 – 5 * i * 5 * i) =

= (2 + 3 * i + 10 * i – 15) / (1 + 25) = (-13 + 13 * i) / 26 = -0,5 + 0,5 * i.

Стоит обратить внимание, что при совершении арифметических операций над комплексными числами, выполняемые действия аналогичны к тем, которые производятся при преобразовании многочленов (двучленов). Однако не следует забывать, что при возведении в квадрат комплексного числа i, в результате всегда получается число -1.

Ещё одним важным нюансом при вычислении частного комплексных чисел является необходимость умножать числитель и знаменатель дроби, полученной при записи частного, на выражение (комплексное число), которое является сопряженным к знаменателю.

На этом этапе достаточно просто убедиться, что мало знать комплексные числа, нужны ещё формулы сокращенного умножения, которые позволяют получать упрощенное выражение (которое преобразуется в действительное число), в знаменателе дроби.

Тригонометрическая форма записи комплексного числа

Приведенную выше информацию можно назвать «комплексные числа для чайников». Она включила информацию про комплексные числа кратко представленную в доступной для читателя форме.

Если же есть необходимость углубляться в теорию комплексных чисел, то тут уже стоит рассматривать тригонометрическую форму записи комплексного числа. Она представляет собой выражение вида r * (cos(f) + i * sin(f)).

В представленном выражении появляются новые обозначения помимо хорошо известных тригонометрических функций косинус и синус, которые находятся от угла f.

Итак, именно с угла f и начнем пояснение. Величина f для комплексного числа это угол наклона вектора, который характеризует комплексное число. Рассмотренная величина называется аргументом комплексного числа и используется не только в тригонометрической, а и в показательной форме записи комплексных чисел. Она может принимать как положительные, так и отрицательные значения.

Теперь вернемся к первому множителю, который указан в тригонометрической форме записи – множитель r. Эта величина r называется модулем комплексного числа. Для его вычисления необходимо найти корень квадратный из суммы квадратов действительной и мнимой частей комплексного числа. При извлечении корня, находят арифметический квадратный корень, поэтому полученное значение величины r всегда будет только положительным (больше нуля).

Тригонометрическая, как и показательная формы записи комплексного числа необходимы в первую очередь для проведения таких операций над комплексными числами как извлечения корня комплексного числа, а также возведения комплексного числа в любую степень.

Безусловно, если говорить про алгебраическую форму записи, то возведение в степень будет доступным, но уже при возведении в степень большую чем, например, третья, будут возникать неудобства вычисления.

Возводя же в любую степень комплексное число в тригонометрической форме, достаточно в эту степень возвести модуль комплексного числа, а его аргумент – умножить на указанный показатель степени. В случае получения достаточно больших значений для аргумента, их без труда можно уменьшить, используя периодичность тригонометрических функций синус и косинус.

При правильном подходе видим, что комплексные числа являются достаточно простой темой, а действия над ними схожи с теми действиями, которые выполнялись при изучении таких тем курса алгебры и начал анализа как:

• Тригонометрические функции;
• Степенные выражения и действия над ними;
• Многочлены и действия над ними.

Из истории о комплексных числах

Развитие понятия числа от натуральных к действительным был связан как с нуждами практики, так и с нуждами самой математики. Древнегреческие математики считали «настоящими» лишь натуральные числа, но в житейских расчетах за тысячи лет до н. э. в Древнем Египте и в Древнем Вавилоне уже применялись дроби. Следующим значительным этапом в развитии понятия о числе было открытие отрицательных величин. Их ввели китайские математики за два века до н. э. а древнегреческий ученый Диофант в III веке н.э. уже мог производить действия над отрицательными числами. В тринадцатом веке стали извлекать квадратные корни из положительных чисел и определили, что с числами отрицательными эта операция неосуществима. Но в шестанадцатом веке в связи с познанием кубических уравнений математики столкнулись с данной проблемой. Исходя из этого итальянский алгебраист Дж. Кардано в 1545 году в собственном труде «Великое мастерство, либо «Об алгебраических правилах» внес предложение ввести числа новой сущности. Он назвал эти величины «чисто отрицательными» либо «софистически отрицательными», но находил их совсем ненужными и пытался не пользоваться ими. Но в первой половине 70-ых годов XVI века его соплеменник Р. Бомбелли опубликовал книгу, в которой были введены первые правила арифметических операций над подобными числами, вплоть до извлечения из них кубических корней.

Наименование «мнимые числа» во второй половине 30-ых годов семнадцатого века было введено философом и французским великим математиком Р. Декартом. А во второй половине 70-ых годов восемнадцатого века один из виднейших алгебраистов 18 века – Л. Эйлер – внес предложение применять первую букву французского слова imaginaire (мнимый) для обозначения числа I = √-1. Сам же термин «комплексное число» ввел в 1803 году Л. Карно, но в оборот он вошел лишь благодаря трудам К. Гаусса. Постепенно расширялась техника операций над комплексными числами. На рубеже 17 – 18 столетий была выстроена общая теория корней n-й степени сперва из отрицательных, а позже из любых комплексных чисел, а подробное геометрическое пояснение «мнимым» величинам дали в собственных трудах К. Вессель и Ж. Арган.

В конце 18 века великий математик из Франции Ж. Лагранж смог заявить, что матанализ уже не затрудняют мнимые величины. Посредством комплексных чисел обучились выражать решения линейных дифференциальных уравнений с постоянными коэффициентами, а Я. Бернулли использовал комплексные числа для вычисления интегралов. Кроме этого посредством «мнимых» величин были решены задачи, которые связаны с гидродинамикой и картографией.

Интересные факты о комплексных числах

В 1572 году появилась книга, написанная великим математиком из Италии Рафаэлем Бомбелли – в этой книги автор описал правила арифметических операций с такими числами, вплоть до извлечения из них кубических корней.

Для многих знаменитых деятелей – учёных XVII века алгебраическая и геометрическая природа мнимых величин представлялась непонятной.

Известно, например, что Исаак Ньютон не включал мнимые величины в понятие числа, а Готфрид Лейбниц высказал: «Мнимые числа – это чудесное и прекрасное убежище божественного духа, почти как амфибия бытия с небытием».