
Треугольник Паскаля
Треугольник Паскаля представляет из себя пирамиду чисел (биномиальных коэффициентов), с основанием уходящим в бесконечность. В этой пирамиде-треугольнике на вершине (1-ряд) и по бокам стоят единицы. Каждое число равно сумме двух расположенных над ним чисел. Строки треугольника симметричны относительно вертикальной оси.
История
Назван в честь Блеза Паскаля. Блез Паскаль ввел свой треугольник в 1653 г. в труде “Traité du triangle arithmétique”, как часть задачи для исследования вероятностей и для вычислений. Задачи были примерно такие: “Если я хочу выбрать двух человек из четырех данных, сколько существует возможных пар?’’ или “Какова вероятность выпадения фулл-хауса (примеч. в покере три карты одного достоинства и две другого), когда раздается по пять карт из колоды, которая хорошо перемешана?’’ Паскаль и Ферма в основном обсуждали вероятность в письмах, которыми они обменивались в то время. Треугольник Паскаля
Изначально треугольник Паскаля выглядел следующим образом:
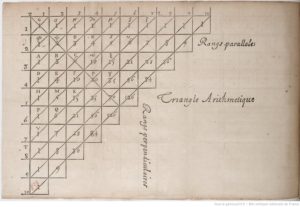
Числа, составляющие треугольник Паскаля, возникают естественным образом в алгебре, комбинаторике, теории вероятностей, математическом анализе, теории чисел.

Закономерности треугольника Паскаля
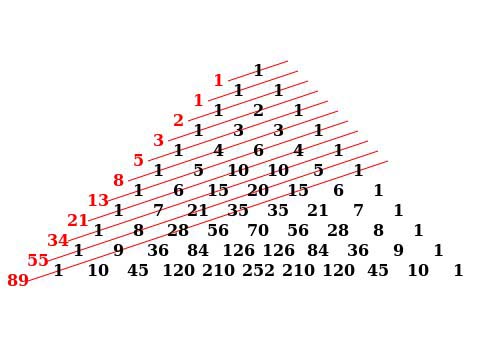
Существует множество интересных закономерностей, связанных с треугольником Паскаля. Например, сумма чисел n-й строки треугольника Паскаля равна 2^n, а сумма чисел восходящей диагонали, начинающейся с первого элемента (n-1)-й строки, есть n-е число Фибоначчи (вторая картинка).
Заметим еще одно красивое свойство. Покрасим каждое число в треугольнике Паскаля в один из двух цветов, в зависимости от того, является оно четным или нечетным. Например, четные числа белым, а нечетные синим. Если мы сделаем это для первых 500 строк треугольника, получим третью картинку – фрактал, известный как треугольник Серпинского (Вацлавом Серпинским в 1915 году).


Число четное или нечетное, если оно при делении на 2 дает остаток 0 или 1 соответственно. Что происходит, когда разделим на 8? Остатки могут быть равны 0, 1, 2, 3, 4, 5, 6 или 7. Что произойдет, если использовать восемь цветов и покрасить каждое число в соответствии с его остатком при делении на восемь? Для первых 500 строк треугольника получим четвертую картинку.
[content-egg module=Youtube]
