Красота формул

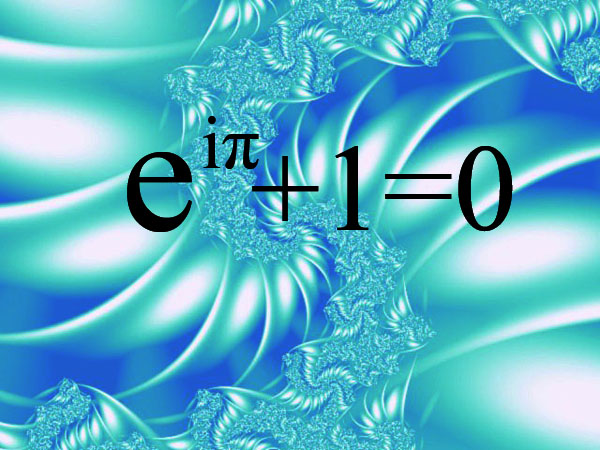
Красота математических формул

Красота – понятие сугубо индивидуальное и особенное. Одни люди в восторге от красоты природы, другим нравится живопись, а кто-то в восторге от музыкальной гармонии. Но есть, на первый взгляд, странные вещи, красоту и эстетический вид которых, как оказалось, можно оценить. Это уже задача для математических «гурманов» – оценка привлекательного вида… математических формул!

Необычные английские нейробиологи настолько увлеклись изучением сущности людей разных профессий, что решили даже сделать своеобразный эксперимент. В настоящее время он касался людей интеллигентных профессий – математиков. Задача оказалась очень простой – им надо было оценить красоту того, с чем они сталкиваются ежедневно. Так, вы, вероятно, правильно догадались – 15 человек, посвятивших свою жизнь изучению математики, оценивали эстетический вид 60 математических формул.

Для оценки результатов своеобразного эксперимента нейробиологи из Великобритании использовали магнитно-резонансный томограф или МРТ, как его часто называют люди. Этот прибор отслеживал отзывы мозга математиков, когда людям показывали различные формулы – хорошие и не слишком по восприятию их бессознательности. Итак, сами математики могли сознательно не знать и не догадываться, что для их мозга одна формула нравится гораздо больше другой.

Что такое красота математических формул?

Таким образом, просмотр красивых формул вызывает своеобразные ощущения и отзыв префронтальной коры головного мозга людей. Знаете ли вы, что отзыв в этой части мозга отвечает за самые сложные когнитивные функции и воспроизведения эмоций. Поэтому можно утверждать, что просмотр красивых математических формул у людей с математическим складом ума вызывает ощущения, которые схожи с теми, что возникают в момент просмотра живописных произведений или прослушивания классической музыки.

Математик Анри Пуанкаре в книге «метод и Наука» писал: «Если бы природа не была красива, она не стоила бы того, дабы ее знать, жизнь не стоила бы того, дабы ее волноваться. Я тут говорю, само собой разумеется, не о той красоте, которая кидается в глаза… Я имею в виду ту более глубокую красоту, которая раскрывается в гармонии частей, которая постигается лишь разумом. Это она формирует землю, формирует каркас для игры видимых красок, ласкающих свои эмоции, и без данной помощи красота мимолетных впечатлений была бы несовершенна как все неотчетливое и преходящее. Наоборот красота интеллектуальная дает удовлетворение сама по себе».

П.А.М. Дирак писал: “У теоретической физики имеется еще один верный путь развития. Природе свойственна та фундаментальная особенность, что самые фундаментальные физические законы описываются математической теорией, аппарат которой владеет неординарной силой и красотой. Чтобы выяснить эту теорию, необходимо владеть очень высокой математической квалификацией. Вы имеете возможность задать вопрос: по какой причине природа устроена поэтому так? На это возможно ответить лишь одно: в соответствии с отечественным современным знаниям, природа устроена поэтому так, а не в противном случае”.

Семь лет назад украинский физик (и живописец) Наталия Кондратьева обратилась к последовательности ведущих математиков мира с вопросом: «Какие конкретно три математические формулы, на ваш взор, самые прекрасные?»
В беседе о красоте математических формул участвовали господин Михаэль Атья и Дэвид Элварси из Британии, Яков Александр и Синай Кириллов из америки, Фридрих Херцебрух и Юрий Манин из Германии, Давид Рюэль из Франции, Анатолий Вершик и Роберт Минлос из России и другие математики из различных государств. Из украинцев в дискуссии участвовали академики НАНУ Владимир Королюк и Анатолий Скороход. Часть взятых так материалов и легла в базу изданной Натальей Кондратьевой научной работы «Три самые прекрасные математические формулы».
— Какую цель вы ставили, обращаясь к математикам с вопросом о прекрасных формулах?
— Каждое новое столетие приносит обновление научной парадигмы. В начале века с ощущением, что мы стоим у порога новой науки, ее новой роли в жизни человеческого общества, я обратилась к математикам с вопросом о красоте идей, стоящих за математическими знаками, т.е. о красоте математических формул.
Уже на данный момент необходимо отметить кое-какие особенности новой науки. В случае, если в науке ХХ века очень ключевую роль игралась «дружба» математики с физикой, то на данный момент математика действенно сотрудничает с биологией, генетикой, социологией, экономикой… Следовательно, наука будет изучить соответствия. Математические структуры будут изучить соответствия между сотрудничествами элементов планов и различных областей. И очень многое, что раньше мы принимали на веру как философские констатации, будет утверждено наукой как конкретное знание.
Данный процесс начался уже в ХХ веке. Так, Колмогоров математически продемонстрировал, что случайности нет, а имеется большая сложность. Фрактальная геометрия подтвердила принцип единства в многообразии и т.д.
— Какие конкретно же формулы были названы самыми прекрасными?
— Сходу сообщу, что цели устроить конкурс формулам не было. В собственном письме к математикам я писала: «Люди, каковые желают осознать, какими законами управляется мир, становятся на путь отыскания гармонии мира. Путь данный уходит в бесконечность (потому что перемещение всегда), но люди всё равняется идут им, т.к. имеется особенная радость встретить очередную идею либо представление. Из ответов на вопрос о прекрасных формулах, быть может, удастся синтезировать новую грань красоты мира. Помимо этого, эта работа может оказаться нужной для будущих ученых как идея о великой гармонии мира и математики как методе отыскания данной красоты».
Однако среди формул были явные фавориты: формула Эйлера и формула Пифагора.
За ними расположились скорее физические, чем математические формулы, каковые в ХХ веке поменяли отечественное преставление о мире, —Максвелла, Шредингера, Эйнштейна.
Кроме этого в число самых прекрасных попали формулы, каковые еще находятся на стадии дискуссии, такие, к примеру, как уравнения физического вакуума. Назывались и другие прекрасные математические формулы.
— Как вы думаете, по какой причине на рубеже второго и третьего тысячелетий формула Пифагора названа одной из самых прекрасных?
— Во времена Пифагора эта формула воспринималась как выражение принципа космической эволюции: два противоположных начала (два квадрата, соприкасающихся ортогонально) порождают третье, равное их сумме. Возможно дать геометрически прекрасные интерпретации.
Быть может, существует какая-то подсознательная, генетическая память о тех временах, в то время, когда понятие «математика» означало — «наука», и в синтезе изучались математика, живопись, музыка, философия.
Рафаил Хасминский в собственном письме написал, что в школе он был поражен красотой формулы Пифагора, что это во многом выяснило его судьбу как математика.
— А что возможно сообщить о формуле Эйлера?
— Кое-какие математики обращали внимание, что в ней «собрались все», т.е. все самые превосходные математические числа, и единица содержит бесконечности! — это имеет глубочайший философский суть.
Недаром эту формулу открыл Эйлер. Великий великий математик много сделал, дабы ввести красоту в науку, он кроме того ввел в математику понятие «градус красоты». Вернее, он ввел это понятие в теорию музыки, которую считал частью математики.
Эйлер полагал, что эстетическое чувство возможно развивать и что это чувство нужно ученому.
Сошлюсь на авторитеты… Гротендик: «Познание той либо другой вещи в математике так совсем, как допустимо прочувствовать ее красоту».
Пуанкаре: «В математике налицо чувство». Он сравнивал эстетическое чувство в математике с фильтром, что из множества вариантов решения выбирает самый гармоничный, что, в большинстве случаев, и имеется верный. гармония и Красота — синонимы, а высшее проявление гармонии имеется всемирный закон Равновесия. Математика исследует данный закон на различных замыслах бытия и в различных качествах. Недаром любая математическая формула содержит символ равенства.
Пологаю, что верховная людская гармония имеется гармония мысли и эмоции. Возможно, исходя из этого Эйнштейн заявил, что автор Достоевский дал ему больше, чем великий математик Гаусс.
Формулу Достоевского «Красота спасет мир» я забрала в качестве эпиграфа к работе о красоте в математике. И он кроме этого обсуждался математиками.
— И они дали согласие с этим утверждением?
— Математики не утверждали и не опровергали этого утверждения. Они его уточнили: «Осознание красоты спасет мир». Тут сходу вспомнилась работа Юджина Вигнера о роли сознания в квантовых измерениях, написанная им практически пятьдесят лет назад. В данной работе Вигнер продемонстрировал, что человеческое сознание воздействует на внешнюю среду, т.е., что мы не только приобретаем данные извне, но и отправляем отечественные мысли и эмоции в ответ. Эта работа до сих пор актуальна и имеет как собственных приверженцев, так и соперников. Я весьма надеюсь, что в ХХI веке наука докажет: осознание красоты содействует гармонизации отечественного мира.

1. Формула Эйлера. Многие видели в данной формуле знак единства всей математики, потому что в ней “-1 воображает математику, i – алгебру, ? – геометрию и e – анализ”.

2. Это простое равенство показывает, величина 0,999 (и так до бесконечности) эквивалентна единице. Многие люди не верят, что это возможно, не смотря на то, что существует пара доказательств, основанных на теории пределов. Однако, равенство показывает принцип бесконечности.

3. Это уравнение было сформулировано Эйнштейном в рамках новаторской общей теории относительности в 1915 году. Правая часть этого уравнения обрисовывает энергию, содержащуюся во Вселенной (а также” чёрную энергию”). Левая сторона обрисовывает геометрию пространства-времени. Равенство отражает тот факт, что в общей теории относительности Эйнштейна, энергия и масса определяют геометрию, и в один момент кривизну, которая ничто иное как проявление гравитации. Эйнштейн сказал, что левая часть уравнений тяготения в общей теории относительности, содержащая гравитационного поля, прекрасна и как словно бы вырезана из мрамора, тогда как правая часть уравнений, обрисовывающая материю, всё ещё некрасива и уродлива, словно бы сделана из обычной деревяшки.

4. Еще одна доминирующая теория физики — Стандартная модель — описывает электромагнитное, слабое и сильное взаимодействие всех элементарных частиц. Некоторые физики считают, что она отображает все процессы, происходящие во Вселенной, кроме темной материи, темной энергии и не включает в себя гравитацию. В Стандартную модель вписывается и неуловимый до прошлого года бозон Хиггса, хотя не все специалисты уверены в его существовании.

5. Теорема Пифагора — одна из основополагающих теорем евклидовой геометрии, устанавливающая соотношение между сторонами прямоугольного треугольника. Ее мы помним еще со школы и считаем, что автор теоремы — Пифагор. На самом деле этой формулой пользовались еще в Древнем Египте при строительстве пирамид.

6. Теорема Эйлера. Эта теорема заложила фундамент нового раздела математики — топологии. Уравнение устанавливает связь между числом вершин, ребер и граней для многогранников, топологически эквивалентных сфере.

7. Специальная теория относительности описывает движение, законы механики и пространственно-временные отношения при произвольных скоростях движения, меньших скорости света в вакууме, в том числе близких к скорости света. Эйнштейн составил формулу, которая описывает, что время и пространство не являются абсолютными понятиями, а скорее являются относительными в зависимости от скорости наблюдателя. Уравнение показывает, как расширяется или замедляется время в зависимости от того, как и куда движется человек.

8. Уравнение было получено в 1750-х годах Эйлером и Лагранжем при решении задачи об изохроне. Это проблема определения кривой, по которой тяжелая частица попадает в фиксированную точку за фиксированное время, независимо от начальной точки. В общих словах, если ваша система имеет симметрию, есть соответствующий закон сохранения симметрии.

9. Уравнение Каллана — Симанзика. Оно представляет собой дифференциальное уравнение, описывающее эволюцию н-корреляционной функции при изменении масштаба энергий, при которых теория определена и включает в себя бета-функции теории и аномальные размерности. Это уравнение помогло лучше понять квантовую физику.

10. Уравнение минимальной поверхности. Это равенство объясняет формирование мыльных пузырей.

11. Прямая Эйлера. Теорема Эйлера была доказана в 1765 году. Он обнаружил, что середины сторон треугольника и основания его высот лежат на одной окружности.

12. В 1928 году П.А.М. Дирак предложил свой вариант уравнения Шредингера – которое соответствовало теории А. Эйнштейна. Учёный мир был потрясён – Дирак открыл своё уравнение для электрона путём чисто математических манипуляций с высшими математическими объектами, известными как спиноры. И это было сенсацией – до сих пор все великие открытия в физике должны стоять на прочной базе экспериментальных данных. Но Дирак считал, что чистая математика, если она достаточно красива, является надёжным критерием правильности выводов. «Красота уравнений важнее, чем их соответствие экспериментальным данным. … Представляется, что если стремишься получить в уравнениях красоту и обладаешь здоровой интуицией, то ты на верном пути». Именно благодаря его выкладкам был открыт позитрон – антиэлектрон, и предсказал наличие у электрона «спина» – вращения элементарной частицы.

13. Дж. Максвелл получил удивительные уравнения, объединившие все явления электричества, магнетизма и оптики. Замечательный немецкий физик, один из создателей статистической физики, Людвиг Больцман, сказал об уравнениях Максвелла: «Не Бог ли начертал эти письмена?»

14. Уравнение Шредингера.Уравнение, описывающее изменение в пространстве и во времени чистого состояния, задаваемого волновой функцией, в гамильтоновых квантовых системах. Играет в квантовой механике такую же важную роль, как уравнение второго закона Ньютона в классической механике.