ГОЛОГРАФИЯ ВСЕЛЕННОЙ

ГЕОМЕТРИЯ ПРОСТРАНСТВА И ВРЕМЕНИ

А. А. Локтюшин

Аннотация

Интересная и глубокая книга сибирского ученого Александра Локтюшина «Голография вселенной: геометрия пространства и времени» продолжает линию, намеченную в его предыдущей книге «Сакральная история цивилизации: экология и этика». На этот раз в центре внимания автора естественно-научная картина мира: книга посвящена теме эволюции мироздания как единого живого организма. Новый взгляд на природу пространства, времени и работу причинно-следственных законов делает эту книгу очень интересным, можно сказать, прорывным исследованием в изучении природы. Книгу отличают необычный, междисциплинарный подход и своеобразный взгляд на многие известные дисциплины. Автор охватывает целый ряд областей: физику, геофизику, биосферные процессы, планетарный климат, географию, топонимику, биохимию, языческие верования нашш предков, христианство, историю.

Книга, написанная в живом, научно-популярном стиле, будет с увлечением прочитана широким кругом читателей, сохранивших интерес к науке и попыткам познать глубинную природу мироздания.

Книга Александра Андреевича Локтюшина, по замыслу автора, задумывалась как «развитие мировоззренческих систем через призму представлений о причинно-следственных связях». Эволюция наших представлений о причинно-следственных связях с неизбежностью приводит нас к восприятию всех явлений окружающего Мира как процесса жизнедеятельности единого живого организма.

Огромная задача! Необыкновенно сложно — и труднодостижимая цель поставлена! И если помнить, что цель как закон определяет способы и средства своего достижения, следует ожидать и столь же сложную форму изложения. И действительно, этот момент присутствует. Но только момент. Читателю уже со средним образованием очень скоро в книге открывается удивительная простота общения с автором. Хотя это простота тех самых сказок, что являются и «намеком и для добрых молодцев уроком». По выражению одного научного сотрудника, многие разделы книги ему напоминают именно «сказку — но для старших научных сотрудников с высшими учеными степенями».

Большой объем и многоплановость книги при жесткой подчиненности одной идее и единообразии изложения (автор предлагает свою работу на суд широкого круга читателей, но научно-популярной ее никак не назовешь) заставляет избегать в предисловии обычного перечисления названий глав и пояснения их содержания. Однако на некоторых идеях и мотивах изложения присутствующих либо явно, либо в неявной форме остановиться следует.

Былинно-легендарный мотив изложения при тщательной проработке фактического архео-, палео-, геолого-исторического, топонимического, географического и лингвистического материалов необыкновенно характерен для первых частей книги — «Экология» и «Этика». Для нас непривычная манера изложения. Мы как-то больше приучены, что в историко-географических исследованиях авторы постоянно ссылаются на те или иные документы, извлеченные иной раз и Бог знает из архивов какой секретности или вековой давности. Особенно это характерно для статей и книг, посвящаемых эпохам географических открытий. Ссылки на «библиографов» экспедиций, как научных, так и завоевательных, считаются чуть ли не основным достоинством таких исследований. Правда, здесь дело доходит до юмористических казусов, ибо наиболее точные и беспристрастные данные о стародавних предприятиях предоставляют нам как раз не «библиографы», а бухгалтерские книги и записи экономов-хозяй- ственников (кто, сколько, когда и чего съел, закупил, украл, отобрал у местного населения и т. д., и т. п.). С «больщой историей» дело обстоит ничуть не лучшим образом. Официальные труды и историков, и «библиографов» стремятся приучить нас и замкнуть нас (читателя) на господствующей в их время общепринятой точке зрения на все и вся. Причем эта точка зрения принята как раз не большинством, а активным власть предержащим меньшинством и только в собственных корпоративно корыстных интересах этого меньшинства. Каковую бы систему мировоззренческих взглядов ни навязывало меньшинство всем прочим.

Но наряду с официальной «памятью» существует неистребимая никакими властями в тысячелетиях другая, великая книга правды-памяти. Память народов. Передаваемая в устных преданиях от прадедов-участников к правнукам-продолжателям, эта память с неизбежностью приобретает легендарно-мифологический оттенок. Сохраняя при этом, как уже не раз убеждались историки, точность не только по содержанию, но и по терминологии. И специалистам по расшифровке различного рода тайнописей-криптограмм давно известно, что лучший способ сохранить и передать информацию — это как раз не шифровки типа «пляшущих человечков» А. Конан Дойля, а смысловое значение сообщения, которое не утрачивается даже при переводе на другие языки. И тому, кто поймет смысл, идею таких сообщения, мифа, легенды, сказки, и открывается простая, нередко великая, правда — тайна!

И именно этим, совсем не легким и отнюдь не примитивным и простым путем ведет автор свое уникальное исследование.

Настоятельно рекомендуем читателю пройти вместе с ним интереснейший путь поиска нашей общей прародины, наших общих предков-учителей, обычаев. Культуры и отношения к простым, но жизненно важным для нас, и древних и нынешних, общечеловеческим нетленным ценностям.

Третья часть книги — «Естествознание» — написана уже для более «специализированного» и подготовленного читателя. Впрочем, и здесь знаний 1-2-го курса любого высшего учебного заведения по математике и физике вполне достаточно. Тем более что основное внимание (при по-прежнему сохранившемся разнообразрш примеров, задач и проблем) уделено двум, по сути, общеизвестным явлениям — резонансу и структуре.

Резонанс нам известен уже из средней школы. Пример — насколько яркий, настолько же и неудачный — также общеизвестен. «Шел полк солдат по мосту, чеканя шаг, случайно частота шага и частота собственных колебаний конструкции моста совпали. Мост рухнул». С тех пор и по сие время воинское подразделение при переходе через мост «сбивает» шаг. Даже команда специально подается. Эффект резонанса, поданный таким вот образом, воспринимается как структуроразрушительный. Хотя, конечно, и в электронике, и в радиоделе резонансные явления используются для усиления слабого сигнала. Но структура! Строение вещества и природных тел «и искусственных» из этого вещества самого различного состава, формы и свойств. Та самая структура, что разрушается резонансом! Что ее создает, что создает тела, обладающие вполне определенным строением? Ведь, несмотря на огромное разнообразие объектов различных строения и формы, влияющих на свойства объектов и обусловливающих их взаимодействие с другими объектами и окружающим Миром, мысль о единообразии всех объектов природы (отнюдь не искусственных!) вовсе не нова. Вплоть до общеизвестного выражения «что вверху, то и внизу». Единообразие структур отмечается буквально всеми. Одна «планетарная модель атома» сэра Резерфорда чего стоит. Однако какой физический агент ответственен за столь разномасштабные и в то же время структурно сходные объекты?

И автор находит его. Это резонанс. Это резонансные взаимодействия между объектами и полями на всех уровнях масштабов — начиная с микромира и кончая объектами планетарного размера. Сразу следует подчеркнуть, что современная физика оказалась не готова к восприятию этой идеи. То, что служило разрушением, оказалось созидательно способным, да еще в столь широком кругу явлений. Но этот вопрос в предисловии разбирать уже не следует. Вот об этом нужно читать в соответствующих главах книги, с карандашом в руках и схемами на экране монитора. Идея структуроформирующего эффекта резонанса, которую автор скрупулезно разбирает с привлечением всех доступных средств математики и физики, обретает четкость и ясность геометрической теоремы. Несомненно, что разработка этого вопроса станет делом будущих исследований тех, кто рискнет войти в соверщенно новую область мировосприятия. БАЗА УЖЕ СОЗДАНА!

Непоправимо рано ушел из жизни человек, чье произведение, публикуемое близкими, друзьями и коллегами, предлагается вниманию читателя. Сложнейшие вопросы мировосприятрм, при высоком научном уровне подаваемого материала, излагаются Александром Андреевичем часто в остроумной, нередко мудро-лукавой манере опытного, много размышлявшего и пережившего человека. Человека, который не навязывает

свою точку зрения, а делится плодами исследований, сложившимися в систему не в результате «складывания», а постепенно вырисовывающую себя в процессе познавания внутренней логики явлений. Первому быть всегда сложно. Согласно печальному опыту из истории науки известно, что именно первому и достается все самое сложное и трудное. НО ПЕРВЫЙ, САМЫЙ СЛОЖНЫЙ, ШАГ СДЕЛАН, И ЦЕПЬ ЗНАНИЙ НЕ БУДЕТ ПРЕРВАНА!

Глава 1.

В названии этой главы заложена, по сути дела, тавтология, ибо современная экология — это не только очень общая научная дисциплина, выросшая из частной биологической гипотезы, но и фршософия, поглощающая собою и естествознание. Другими словами, экология есть естествознание, «доросшее» до очередного фршософско- го обобщения. До уровня общенаучного мировоззрения.

Более естественным названием этого раздела бьшо бы привычное «введение», но и все это сочинение есть не что иное, как введение, которое так и называется: Пропедевтика. Звучит несколько по-иному, но только как дань памяти классикам. Всем сразу. Поэтому, хотя в тексте и будут упомянуты некоторые славьахе имена, но привычного для научной работы или учебника списка литературы здесь не найти. Бьшо бы неправильно привести указания на несколько сотен публикаций, когда на самом деле их десятки (а может, и сотни) тысяч. И вообще это задача, может быть, для специального библиографического исследования. У нас несколько иная цель.

Экология интенсивно начала развиваться в последней трети двадцатого века в связи с обострением некоторых проблем в отношениях человека с окружающей средой. Поэтому большинство из многочисленных исследований замыкаются в кругу частных проблем. Энергетика, мусор, социальная напряженность и т. п. Иногда и попросту экологический «слоган» используется в чисто спекулятивных эшномических или политических целях. Очень популярна, например, тема теплового загрязнения атмосферы, которой посвящаются околонаучные семинары с участием глав государств. Но при ближайшем рассмотрешш за этим шумом нетрудно разглядеть желание торговать «воздухом». На самом высоюм уровне с водой уже «справились». Питьевую воду продают в бутылках по «приличной» цене. И заняты этой темой самые высокопоставлегшые международные политики и чиновники. Что, впрочем, вполне естественно, посколы^ все огш ангажированы (готшены) хозяевами финансового капитала А тем, в свою очередь, совершегшо не интересно заниматься работой по классической схеме: «… — товар—деньги—тов^)—деньги —…». Куда проще: «Деггьги делают деньги».

Очень большое сомнение в чистоте помыслов вызывает и деятельность многих «природоохранных» фондов и общественных организаций. Однажды на вопрос, что такое движение «Гринпис», один из студентов на весьма специфическом сленге, но очень емко и четко сформулировал: «Это куда одни паханы бабки башляют, чтобы другим фирмы повалить».

Вместе с тем обострение экологических проблем существует реально, но, во-первых, имеет локальный по историческим меркам характер и, во-вторых, носит преимуще- ствегшо нравственные оттенки. И, тем не менее, именно этому спекулятивному периоду развития мы обязаны осознанием глобальности значеггия экологических ггрингщпов.

Предшествующие общенаучные парадигмы — механицизм и позггтивизм — возникали как бы по инерции

развития частных разделов естествознания в результате обобщения своих принципов до «философии природы». И в этом отношении современный этап мало чем отличается. Ведь экология — это тоже естествознание, по крайней мере, часть его. А значит, «принципы» уже существуют, и следует их только вычленить и обобщить. Поэтому совершенно не удивительно богатство предложений такого рода, возникших в последней трети двадцатого века параллельно с развитием экологии. Здесь можно было бы уделить много места обсуждению очень красивых и плодотворных идей, претендующих на общенаучное значение. Синергетика, макрокинетика, неравновесная термодинамика, теория фракталов и пр. Но, как правило, эти новые концепции — всего лищь полированные грани все той же позитивистской парадигмы. За исключением, быть может, теории фракталов, являющейся, по сути, «прикладным» развитием теории комплексного переменного и восхищающей кружевами узорчатых картинок, смысл которых «надо бы еще придумать». О комплексности окружающей реальности мы еще обязаны порассуждать. Но несколько позднее.

Существует (возникли) и целый ряд более радикальных предложений по возврату к механистическим принципам. К «механическому» эфиру. Конечно, в силу принципа соответствия и эти модели «устройства мира» обладают реальной ценностью и иногда могут быть весьма продуктивными. Но в целом это движение очень напоминает экологические лозунги: «Назад к природе!». Сюрреализм. Кому захочется в здравом уме покинуть благоустроенную квартиру со светом, ванной и теплым унитазом, чтобы поселиться в «пещере». Да и пещер на всех не хватит. А если вдуматься, то современное жилье мегаполисов мало чем отличается от пещер, а улицы городов — от джунглей.

Самый богатый «рьшок» парадигмальных естественнонаучных предложений порояоден воспаленным сознанием насущности революционных перемен и невинной наивностью. Наиболее заметные, может быть, идеи этого плана: ми1фолептонные поля, космические струны, биополя… Наряду с пакетом концептуальных теорий последняя треть ущедшего века сформулировала и набор краеугольных проблем естествознания. Десятка два: — Скрытая масса Вселенной. — Наблюдаемые звезды и туманности составляют всего лишь около 10 процентов от вычисляемой массы. — Начальное состояние Вселенной —Большой взрьш.—Как редуцировать биологические законы к более «простым» физическим. — И так далее.

За этим набором как-то потерялись «мелкие» проблемы: а что такое масса; сила; заряд; время; пространство?

Вместе с тем логика развития естествознания подсказывает, что ответы на большинство и глобальных, и «мелких» (но очень принципиальных) вопросов уже содержатся в достигнутом знании. Можно показать, например, несколько ярких случаев, когда в одной отрасли науки проблема изучена, что называется, насквозь, а специалисты другой просто не знают об этом, хотя остро нуждаются (не подозревая, в чем).

Одна из таких ситуаций уже упоминалась в первой части. Речь идет об эффектах адиабатического размагничивания парамагнитной среды. В результате этого процесса среда охлаждается. Явление хорошо изучено в электродинамике и прикладной физике. Атмосфера (воздух, а точнее, кислород, которого до 21 процента) как раз и является хорошим парамагнетиком, который находится в магнитном поле Земли. Последнее хотя и считается постоянным, но очень изменчиво. Вплоть до возможностей переполюсовки. И поэтому температура атмосферы, а соответственно, погода и климат очень сильно зависят от состояния магнитного поля. Но метеорологи, предметом исследования которых является климат, об этом «не знают», похоже, вовсе.

Таких примеров великое множество. Причины коллизий многообразны. Можно сослаться на недостатки образования. И это правильно. Но можно указать и на психологию восприятия. Ибо человек слышит и видит лишь то, что узнаваемо. Все это относится к частным вопросам, но и в равной мере к фундаментальным пара- дигмальным проблемам. Большинству читателей наверняка хорошо известна диалектическая схема развития: тезис — антитезис — синтез. Но для большинства иссле- дователей-естественников это просто философская «заумь», никакого отношения к его работе «не имеющая». Тем не менее, любая «самая ничтожная» задача решается именно по этой логике, осознанно или бессознательно. Например, сначала формулируется рабочая гипотеза (тезис), которой «противостоят» эксперимент или литературные данные (антитезис), и из сопоставления (часто этот момент называется «обсуждение результатов») возникает синтез. Может быть и наоборот. Сначала эксперимент, а потом гипотеза. Но это либо в том случае, когда эксперимент делается по чужой воле (руководителя), либо по совершенной глупости или воле случая.

Диалектический метод обладает высокой универсальностью (инвариантностью) по отношению к классу сложности рассматриваемых систем и имеет непосредственное отношение к комплексному устройству окружающего

мира, что следовало бы обсудить более детально. Ведь неслучайно «отцы» диалеиики (Гегель) и теории комплексного переменного (Риман) были современниками.

Обращаясь к эволюции общенаучных мировоззрений в эпоху создания современного естествознания, нетрудно увидеть все ту же логику. Первый этап: мир устроен по жестким принципам причигаости. Как механическая машина. И это исходный тезис. Затем последовал второй этап: полный отказ от причинности. Миром правит случай. Антитезис. Теперь на повестке дня — синтез.

Что является основой синтеза? Проблемы химического «синтеза» мы рассмотрим позднее и детально. Но интуитивно понятно, что синтез возможен лишь тогда, когда и в «тезисе», и в «антитезисе» есть совпадаюпще («стыкующиеся») «детали». То есть нечто неизменное — инвариантное. В отношении естествознания это уже рассматривалось в первой части. Инвариантным методом описания процессов и явлений времен механицизма и позитивизма бьша теория волн и колебаний, для которой «безразлично», что «волнуется» или «колеблется».

Большинство задач в теории волн решается из условия, что сами волны не взаимодействуют. Их взаимодействие становится существенным лишь в присутствии вещества, то есть сред со специфическими нелинейными свойствами. Нелинейностью называют непропорциональный отклик на «возмущающее» «покой» среды воздействие волн.

Здесь мы, собственно, и подошли к основной краеугольной проблеме естествознания: что такое вещество? Ибо, имея ответ на этот вопрос, все остальные обозначенные и не названные «фундаментальные» проблемы мы смогли бы увидеть в совершенно ином и, возможно, ясном облике.

Глава 2.

ПРЕДИСЛОВИЕ

ЭКОЛОГИЯ И ЕСТЕСТВОЗНАНИЕ

ГОЛОГРАФИЧЕСКАЯ МОДЕЛЬ ВЕЩЕСТВА

МАТЕРИЯ

Сзоцествует две крайние точки зрения на окружающую реальность. Материализм и Идеализм. Первая исходит из посылки, что материя вечна, существует изначально и лиып> многообразна в своих преобразованиях и проявлениях. Вторая полагает, что ничего материального нет вообще и все окружающее — это лшпь некие образы Высшего Абсолюта — Духа. Первая точка зрения (вернее, те, кто ее придерживается) «на дух» не переносит рассуждений о душе. Боге и т. п. «нелепостях». Вторая — не менее категорична в отношешш «глупостей» материалистов и впадает в крайний фатализм, ибо «Все в руце Божией» и «Всё по воле Божьей». Этот «антагонизм» очень характерен для европейской цивилизации и в ряде многих других проблем. Например, логика европейца не выходит за рамки однозначных ответов <ща—нет». Или в отношешш социальных систем: либо рьшочная, либо плановая (и почему-то тоталитарная). В свете предшествующих рассуждений о диалектике, надеюсь, нетрудно в этом максимализме рассмотреть юношеоюе состояние, не «дозревшее» до стадии синтеза. Собственно, в этом «идеологичеоюм» противоборстве как в зеркале отражается состояние естествознания. Но так и должно быть.

Иногда говорят, что «черно-белой» логике Запада (Европы) противостоит духовность Индокитая, где отсутствуют крайности. Противостояния здесь никакого, конечно, нет. Буддизм и индуизм находятся, вероятно, в фазе «синтеза», но дело в другом. Европейская цивилизация стремительно обращает Индокитай в подобное себе потребительское общество. И, несмотря на некоторую специфику Востока, приобщение к материальным «ценностям» и технологиям Запада неизбежно деформирует мировоззрение. То есть «синтез» якобы не устоял. Можно говорить и о том, что буддизм и индуизм выходят на новый круг развития. Однако все представляется гораздо проще. Хотя и буддизм, и индуизм во многом еще сохраняют признаки философских систем, но системность знаний для основных масс народа утрачена. Может быть, для некоторых монастырей и школ обладание сокровенным (тайным) знанием все еще является основным смыслом бытия, а для крестьянина и ремесленника долетают лищь «крощки со стола» в виде догм, наставлений и ритуалов. Для них это не философия, а в рафинированном виде Вера — религия. А Вера, не опирающаяся на знание, — это просто «упряжка» для толпы.

Но вернемся к предмету параграфа. Эволюция представлений об устройстве самого вещества, уже безотносительно к вопросу о том, «что первее», подчиняется все той же диалектической логике. Здесь различают, в примитивизме, две точки зрения. Первая — вещество (среда) непрерывно. Столь «одиозное» представление (хотя в обьщенной жизни оно вполне удовлетворительно — разве можно представить себе воздух или воду в виде дискретных отдельных частиц?) давно «преодолено» развитыми молеьсулярно-атомистическими уче- НР1ЯМИ. Вода состоит из молекул, а те, в свою очередь, из атомов водорода и кислорода. Мы даже знаем, что молекула воды состоит из двух атомов водорода и одного — кислорода. Вот уже здесь, вполне возможно, мы имеем дело с заблуждением, потому что мы наверняка знаем лишь то, что число атомов водорода относится к числу атомов кислорода как два к одному. А вот «молекул» воды, удовлетворяющих этому соотношению, может быть великое множество.

Идеи сплошных сред весьма удобны при решении множества вполне научных задач. Но это считается лишь грубым приближением или, как принято говорить, модельным представлением. Вроде бы как в мировоззренческом статусе и примате дискретности (атомистичности) вещества никаких сомнений нет. Вторая точка зрения победила окончательно. Только почему вода льется струей, а не разлетается на отдельные молекулы? Наивный вопрос, скажете. Любому щкольнику известно, что существуют силы межмолекулярного взаимодействия (вандерваальсовы, например). Отлично! Все-таки вода «благодаря» Ван-дер-Ваальсу оказывается хоть чуть-чуть ближе к повседневному представлению сплошности, и ни одну из «крайних» точек зрения не стоит выбрасывать «на помойку».

На самом деле отношения «сплошности» и «дискретности» имеют невообразимо сложный <осарактер» и несводимы к однозначному определению. Наивным оказался чисто атомистический подход — вещество в виде матрешки. Тела состоят из молекул, молекулы — из атомов. .. Атомы, казавшиеся неделимыми исходными состояниями — кирпичиками (само слово «атом» переводится как «неделимый») вещества, вдруг, оказалось, имеют сложное внутреннее строение. Сортов атомов всего-то чуть больше сотни, если не считать всякие там изотопы.

Изучение внутреннего устройства атомов поначалу очень обнадежило сторонников «матрешки»: атомы состоят из «легких» электронов и «тяжелых» протонов. Потом для объяснения устойчивости атомного ядра понадобился (и вскоре был открыт) нейтрон. Что-то похожее на протон, только без электрического заряда. А затем «понеслось». Элементарных частиц обнаружилось в числе, значительно большем, чем число самих атомов. Больше десяти тысяч. Возникла проблема систематизации и классификации. Прямо как в зоологии или ботанике.

Но теоретики «не дремали». Оказывается, что свойства многих элементарных частиц можно объяснить, если представить, что они имеют и собственную внутреннюю структуру из тяжелых частиц с дробным электрическим зарядом — кварков. Вначале кварков бьшо всего три. Напомним, что и элементарных частиц поначалу бьшо три: электрон, протон, нейтрон. Затем понадобились и иные. Чтобы в новом «хозяйстве» не заблудиться, их стали классифицировать, приписывая воображаемые цветовые и обонятельные (ароматные) качества. Наряду с тем, что кварки до сих пор не обнаружены экспериментально как самостоятельные отдельные частицы, весь этот цветной и пахучий хоровод очень похож на элементарную издевку над здравым смыслом. Легко предположить, что следующим шагом в данном направлении должно быть «изобретение» частиц, из которых состоят кварки. И так далее. Лабиринт. Но ведь что интересно, так это то, что построены эти «конструкции» на вполне реальных экспериментальных фактах. Точнее, на их интерпретациях. Действительно, ведь во внутренней структуре элементарных частиц есть нечто, что описывается представлением кварков. И стоит задаться вопросом: а не открывает ли эксперимент иных «проходов в лабиринте», мимо которых проскочили сторонники «крайней дискретизации» вепзества?

Слово «дискретность» имеет весьма поучительную этимологию. Приставка «дис» придает основному корню «крет» отрицательное значение «не». «Крет» происходит от слов «творить», «творение». То есть термин «дискретный» имеет значение «несотворенный». Это вполне материалистично в примитивном смысле. Но приставка «дис» двусмысленна. Ее второе значение — двойной, дву-. И «дискретный» превращается в «имеющий двойную природу», «двусотворенный». На первый взгляд кажется, что это лингвистическое упражнение не имеет отношения к предмету обсуждения. Тем не менее, вещество имеет как раз двойную корпускулярно-волновую природу. Поучительность этого забавного пассажа состоит в том, что термины, прижившиеся в словесном обиходе, заключают в себе гораздо больший смысл, чем лежащие на поверхности. Впрочем, можно к этому серьезно не относиться, считая это игрой и каламбуром. «Дискретность» к тому же однозначно перекликается (в глагольной форме) со словом «дискретизация», имеющем значение «опорочивать, лищать доверия».

Не «лучшую», но тоже весьма прозрачную этимологию имеет и термин «корпускула». Здесь «корпус» соответствует понятию «тело», и «корпускула» — уменьшительному «тельце». Но в слове «тело» «корпус» приставка «кор» означает завершенность чего-либо, а корень «пус» — однозначно гной. Отсюда и соответствующее представление о теле как о чем-то «предназначенном» к тому, чтобы сгнить, обратиться в прах. Замена огласовки «у» на «а» приводит к понятию «переход» или «проход» к смысловой нагрузке: корпус — преходящий, бренный. Что, впрочем, одно и то же. Этимологические «раскопки» приводят к «идеалистическому» пониманию терминов «дискретный» и «тело» в смысле характеристик материи как иллюзорной или, по крайней мере, временной (не вечной) субстанции. Не сильнее этого смысла и «фрагментарное» — частица. Часть. Отрывок от чего-то. Тем не менее, надо отдать должное физикам двадцатого столетия. Они «благополучно ушли» от вечной дискуссии материалистов и идеалистов, определив совокупность свойств материи синтетическим понятием «корпускулярно-волновой дуализм» (двойственность).

Реальное вещество имеет признаки и частицы, и волны. То есть ршогда проявляет свойства дискретного тела, а иногда «аморфные» свойства волны. Или все гораздо проще и все проблемы в интерпретации. Нам удобно пользоваться привьганым понятием ограниченного в пространстве тела (собственное, например), и мы пытаемся одеть в эту «шубу» все иное. Хотя прекрасно чувствуем, что естество человеческое не ограничено границами тела. Возвращаясь к понятиям «частица» и «волна», можно увидеть удивительную смысловую инверсию. Бренное, иллюзорное тело — частица представляется чем-то фундаментальным. А волна — это нечто вроде суеты, мимолетного возмущения. Хотя этимология термина «волна», в отличие от рассмотренного происхождения понятий «тело — частица», не допускает и близко уничижительного представления. Здесь явно звучат русское «воля» и иноязычное «хорошо, здорово, крепко, полный, целый». Вполне уместное замещение согласных «в — б» приводит к пониманию божественного вола — быка — тура — Тора. И лишь чуть-чуть вульгаризирует совершенство волны, ее обыденность — всеобщность — обыкновенность — обычность. Последний перевод — «вульгарный» — обычно заставляет задуматься о том, насколько похабно мы относимся к языку. И латинское «вульгарный» и русское «обычный» прямо восходят к божественному Быку. «Оббычий» или «обычай» содержат усиленное указание значимости. «Об» — старший, главный, «Бычий»… и так ясно, если чуточку вспомнить мифологию. Но, как говорят, к хорошему привьпсаешь быстро. Перефразируем и получим другую поговорку: «Что имеем, не храним…».

А, тем не менее, фаеты — вещь упрямая. Если «очистить зерна от плевел», во всем многообразии экспериментальных результатов останется немногое. А именно то, что при взаимодействии электромагнитных волн достаточной интенсивности могут родиться частица и античастица. Например, электрон и позитрон, отличающиеся знаком электрического заряда. Или так же отличающиеся протон и антипротон. До их рождения бьши только волны, но и после их взаимодействия—аннигиляции — остаются только волны. И эти хорошо установленные экспериментальные факты заставляют усом- нрпъся во многих спекуляциях относительно природы вещества. Было только электромагнитное поле и остается только электромагнитное поле. А, следовательно, если «не плодить сущности без нужды», следуя совету Оккама, то все свойства вещества (как и само оно) есть лишь

проявление некоторых структурных особенностей Поля. А поскольку частицы рождаются из электромагнитного поля и, умирая, оставляют после себя лишь электромагнитное поле, то, вероятно, и незачем искать другие виды полей, присмотревшись получше к электромагнитному.

Кстати, «перескакивая» от понятия «волна» к понятию «поле», стоит еще раз изумиться силе и судьбе Слова. Нетрудно заметить этимологическую близость этих терминов. «Волна — воля — вол», а при замене «в — ф» и английское «field — поле», встают в один ряд. Не зря, видимо, в летописях «Поле» писалось с большой буквы.

ПОЛЕ

Ни материалисты, ни идеалисты не отрицают реальности невещественной компоненты окружающей действительности, с одной стороны, и самого вещества — с другой. За исключением, может быть, некоторых ортодоксов. Но это скорее уже не вопрос знания (гносеологии ли), а психологической патологии.

Материалисты полагают материей не только вещество, но и поля, ответственные за взаимодействия в нем. Однако последовательный материалист и сами поля выводит из вещественных субстанций. Можно, например, вообразить совершенно «тонкое» вещество, скажем, в виде шариков с диаметром в миллионы раз меньшими по сравнению с размерами атомного ядра. Соударяясь, эти шарики, подобно газу в молекулярно-кинетической теории, произведут все наблюдаемые в реальном эксперименте эффекты. На этом пути сделано немало правдоподобных и поучительных выводов об устройстве атомов, молекул и т. д. Но это очень напоминает известный флогистон — теплород. И для описания самого этого эфирного «газа» совершенно необходимо ввести еще более тонкое вещество. Эфир-2. А потом и эфир-3, и т. д. Опять «матрешка» безысходности-бесконечности. Но это вовсе не означает бессмысленности подхода. Результаты, полученные, например, Ацюковским, удивляют изяществом следствий и точностью количественных оценок.

Впрочем, последовательные идеалисты недалеко ушли от материалистов в описании тонких моментов генезиса окружающего мира, объявив их прерогативой трансцендентного Начала, Надмирного Духа и т. п. То есть чем-то таким, что недоступно человеческому уразумению. По сути, современные околонаучные материалисты и идеалисты в рафинированном виде отличаются лишь именно отношением к принципиальной познаваемости окружающей реальности. Если материалист питает себя надеждой шаг за шагом приблизиться к самому Началу Начал, то идеалист — принципиальный агностик, считающий некоторые вещи не его ума делом. В этом подходе, конечно, есть здравый смысл, ибо и в повседневной жизни много обстоятельств и проблем, преодолеть и решить которые проще всего «закрыв глаза». Иногда это делают, к сожалению, «насовсем» с помощью веревки или других «лекарств».

Желание познать или, напротив, его отсутствие — это проблема свободы выбора. Но здесь материалистическое стремление гораздо ближе к божественному промыслу, нежели идеалистическое самоограничение. Ибо в Святых Писаниях сказано: «…и пожелал Бог в ту пору постичь себя. И не было причин не сделать этого…».

Если продолжить разбор современных представлений о веществе, то можно увидеть удивительные вещи, связанные с подменой понятий. Когда стало ясно, что взаимодействие между частицами через посредство полей осуществляется дискретными порциями (квантовая теория Планка), то почти немедленно возникло очень живучее и хорошо формализованное представление, что эти порции-кванты есть свойство самого Поля. Оно якобы состоит из частиц. Ныне существует уже целый пантеон таких частиц: гравитоны, ответственны за тяготение; фотоны — за электромагнитное взаимодействие; мезоны — за внутриатомное; глюоны — за внутриядерное. Иногда это ‘очень удобно. Но первоначально прозрачное понимание дискретности именно взаимодействий совершенно «безответственно» перенесено на эту «непонятную субстанцию», ответственную за взаимодействие. Зато остались одни частицы. Опять удобно. Почти такая же ситуация, как и с газоподобным эфиром. Взяли и «вычеркнули» Поле из рассмотрения. «Закрьши глаза».

Желание исключить Поле из анализа легко понять, поскольку это столь же трудная для понимания категория, как, например, и Время. Впрочем, не лучше обстоит дело и с другой, сопряженной со Временем, категорией — Пространством.

Здесь вполне уместно было бы начать новый параграф с традиционным для большинства исследований подобного рода названием: Пространство и Время. Однако добавить что-то новое к огромному количеству мудрствований (софистики) на эту тему довольно сложно. Хотя соблазн присоединиться к сонму Великих софистов велик, по той простой причине, что подавляющее большинство функций, описывающих так или иначе окружающую реальность, имеют в качестве независимых аргументов именно пространство и время. А любые функции (в математически формальном значении) есть, в конечном итоге, всего лишь преобразования аргументов. То есть некоторый набор «деформаций» самих аргументов. Их сжатие или растяжение, да еще некоторое скручивание или вращение. Поэтому очень привлекательны попытки конструирования и полей, и всего окружающего многообразия из чисто геометрических соображений, что составляет предмет геометродинамики.

В последнем направлении, которое является прямой альтернативой вещественно-«частичному» описанию (опять классические тезис и антитезис), достигнуты тоже очень впечатляющие результаты. Уиллер, например, показал возможность существования «массы без массы и заряда без заряда». То есть это попросту некие характеристики структуры пространства. В описании структур пространства очень элегантны конструкции минералога Руднева, полученные с привлечением многомерных и замкнутых пространств. Он смог показать естественность таких свойств реальных тел, как ограниченность в пространстве и неоднородность (дефектность) структуры.

Геометродинамический подход очень симпатичен и, как теперь ясно, весьма продуктивен. Но постоянные трудности, связанные с необходимостью (и неопределенностью) физической интерпретации математических результатов, т. е. попросту придания им физического смысла, заставляют внимательнее приглядеться к набору аргументов. И здесь оказывается, что физический смысл не возникает сам по себе в результате чисто математических ухищрений в виде введения новых размерностей или постулатов. Последний термин и вовсе не дает успокоительного взгляда на математику и теорию вообще. В нем явно усматривается родство с чем-то пустым или желанием прикрыть пустоту (наготу?). А латинское «пустула» переводится совсем скверно: «прыщ, гнойник».

Более того, уже классические канонические уравнения движения включают в структуру своих аргументов, в явном или неявном виде, скорости или импульсы, то есть, вообще говоря, не геометрические характеристики. А в теории относительности, как бы мы к ней ни относились, зависимость геометрических параметров от наличия физических субстанций становится вполне очевидной. Поэтому нет особого смысла надеяться, что можно исследовать отдельно Поле, например, и Пространственно-временной континуум. В последние десятилетия, наряду с настойчивыми попытками создания единой теории Поля, в которой хотелось бы органично описывать известные классические поля: электромагнитное, гравитационное и ядерное, возник целый ряд новых полевых понятий. Биополе? Микролептонные поля? Торсионные и пр.

Здесь возникает желание остановиться и вдуматься в этимологию термина «Поле». В русском языке «поле» происходит от понятия «полый — пустой». Вполне правомерна, вероятно, и следующая цепочка замен согласных, приводящих к тождественному западноевропейскому понятию: поле ^ phole —> hole —> пустой. Но поле в немецком Feld и английском field, и опять слышится фол — пустой. Хотя в то же время немецко-английское

звучание «поля» выводят на совершенно «иное» поня- тае: file — связка, веревка и еще содержание (связное) чего-либо. Возможно, этот пассаж достоин критики, но вновь ярко показывает, что старики (star = звезда и старый человек = старец, сокровищьшца мудрости), творившие Слово, обладали весьма глубокими познаниями.

ПУСТОТА

В индуизме и буддизме, корни которых питаются в безначальных Ведах, понятие «Пустота — Великая Пустота» равноценно понятию Всевышнего Бога. То есть, по сути, это Одно и То же. Один, Тот (тотальный, общий, единственный) — это вновь Имена той же самой Великой Пустоты, которая и есть Бог. Другое имя Пустоты — Шунья — подчеркивает нерасчленимое единство индивидуального Я и Всевышнего (в образе солнца Сан); Шун (Сан) — и — Я. Лао-Цзы использует очень синтетическое утверждение равенства Хаоса (Дао) и Пустоты: «Дао воистину Пусто».

Великая Пустота — это и есть Начало всех Начал. Великое Все и одновременно Ничто. Чуть позже постараемся осознать глубину этого ведического положения, а здесь подчеркнем, что Пустота вовсе не равноценна понятию «пространство». Пространство и Время — всего лишь аспекты проявления Пустоты. Причем не первичные. Они появляются в результате Действия. А до него аспектами Пустоты были и есть Внимание и Восприятие. Обращение Внимания в Восприятие (Действие) порождает Время. И обратное. Действие (обращение Восприятия во внимание) порождает Пространство. Так повествует миф. Но эти образы пока трудны для понимания, хотя ясно, в конечном итоге, что Пространство непрерывно превращается во Время, а Время — в пространство. И этими превращениями своими производят они Свет. Точнее, не производят, а являются им. Здесь слово «являются» следует понимать, видимо, и в смысле «есть», и как «представляются». Если, пренебрегая глубиной мифа, скользить по его поверхности, то очень удобно воспользоваться не менее древним утверждением из «Тибетской книги мертвых»: «Свет имеет природу Пустоты, а Пустота — природу Света».

В данном случае, вероятно, под Светом следует понимать электромагнитное поле в самом широком смысле. А если несколько примитивизировать миф, то следует сделать вывод, что Пространство и Время есть свойства Света. В данном случае Свет становится эквивалентом Пустоты, то есть Бога. Поэтому очень часто встречающееся в Святых Писаниях утверждение: Бог есть Свет — надо, видимо, воспринимать не как гиперболу, а буквально. Кстати, очень многие сентенции Писаний надо понимать буквально. Например, твердь небесная. Ацюковский в «Общей эфиродинамике» вполне убедительно показывает, что это действительно очень упругая субстанция, хотя и газоподобная. Но оставим разбор Писаний теологам и обратимся к языку естествознания.

СЕЧЕНИЯ

В одной старой и мудрой книжке встречается следующее наставление адепту: «Изучай беспристрастно учения иных сект». Этимологическое родство слов «сечение» и «секта» очевидно, и идея этого короткого параграфа заключается в том, чтобы еще раз напомнить об относительности всякого Знания.

Во-первых, потому, что оно всегда зависит от точки зрения, ракурса, а поскольку жизненные обстоятельства у всех исследователей различны, то и взгляд на предмет изучения неизбежно имеет отличия от всех иных. Каждый видит лишь проекцию или сечения. Иногда они почти совпадают. Но это лишь в случае простых предметов. А иногда совпадение лишь частичное, по очень ограниченной линии пересечения. Это гораздо чаще. Конечно, можно выбрать и такие проекции или сечения, которые не будут иметь ничего общего, хотя могут быть вполне правильными и истинными. Например, врач-паразитолог Астафьев строит «модель живой единой Вселенной» сообразно своей профессии и делает это всерьез и изящно. И правильно, скорее всего. Но это его ракурс, сечение. Позволительно и другое мнение — сечение. С точки зрения геометра Вселенная — набор пространств многомерных и искривленных, а для теолога Вселенная — это вопрос живой этики самопозна- ющего Духа. И это правильно. Анри Пуанкаре в свое время очень прозорливо подметил, что «если есть одно объяснение явления, то неизбежно существует их (объяснений) бесчисленное множество».

Но всякий, кто хоть мало-мальски знаком с чертежами, хорощо знает, что для полного представления изображенного необходимо несколько, по крайней мере, проекций и сечений. Отсюда и справедливость древнего наставления. Но очень часто (даже слишком) этому завету не следуют и, ухватив более или менее понятные контуры, полагают их за Истину в последней инстанции. Тогда все вокруг «тупицы» и т. д., и т. п. Это очень распространенная причина для непримиримых «научных» споров, если не простая маски- ровка борьбы за «кормушку».

Изучающему Мир вокруг и внутри себя, вероятно, не следует решать проблему выбора моделей. Надежнее всего не спеша (ибо как говорят на Востоке: спешка от Сатаны), шаг за шагом изучать некоторое количество идей, а затем уж судить, в каком направлении двигаться. Ибо дорог к цели столь же много, как и сечений.

Другая причина относительности знания состоит в том, что человек узнает лишь только то, что знает. Поэтому чтение книг или внимание к речам наставников — это не синтез сечений и проекций в цельное представление, скорее, воспоминания личного опыта, в которых книги и лекции играют в лучшем случае роль подсказок. И каждый исследователь «строит» свое личное (еще одно) сечение. К тому же ни лектор, ни писатель в силу ограниченности своего инструментария просто не в состоянии передать того, что хотят. То есть изъяснение объяснением невозможно, поскольку знание каждого заключено в образах, а не в словах. Отсюда тютчевское сокрушение: «Как беден. Боже, наш язык, хочу, но не могу (высказать)…». И третья причина относительности и неполноты знания заключается в трансцендентности (запредельности) некоторых исходных свойств этого Мира. Можно, например, рассуждать о многом, включая такие тонкие категории, как Пространство и Время. Все «предельно просто». Пространство обращается во время, а Время — в Пространство. И все тут. Но трансцендентность состоит не во Времени или Пространстве, а в том самом их обращении друг в друга. Это некоторое Действие, и какова его природа, указать трудно или попросту невозможно. Хорошо теологам.

Отсюда во всяком исследовании неизбежно принятие некоторой аксиоматической основы, не подлежащей логической проверке. И это принципиально объединяет Науку с Религией.

Аксиоматическая база может быть выбрана достаточно произвольно. Можно полагать трансцендентным Время и выводить из него Действие и Движение. Можно пойти и еще дальше, ограничив себя узкими предметом и методом, а для оправдания позиции, например, использовать расхожую шутку: «Не барское это дело — формулы читать». Но некоторым как раз наоборот, среди формул уютно, и конфузятся они: «теряюсь без них». И это еще одна причина относительности знания, хотя и не принципиальная.

Автор по специальности своей оптик-спектроскопист, и модель Мира, здесь представляемая, неизбежно имеет специфическую оптическую «окраску», скромно называясь «голографическая модель вещества». Здесь наиболее важен поверхностный «технический» смысл прршагательного, поскольку речь идет о голографических эффектах, с которыми мы достаточно знакомы по забавным картинкам, широко используемым для идентификации товаров. Да еще чуть наслышаны об иллюзорных выставках дорогих экспонатов. На самом деле оказывается, что с голографией и голограммами мы имеем очень частое общение, поскольку все вокруг сплощные голограммы и живая голография, а посему и более глубокий смысл последнего термина вполне уместен. Если Холо (Но1о) этимологически означает Пустота, то голография — это и описание Ее, и «письмена» в Ней.

для них Причиной Действия является сам Бог, ибо он и есть Причина Всего.

ВОЛНЫ

Для развиваемой здесь картины (представления) особое значение имеют электромагнитные волны в свете рассмотренных выше замечательных экспериментальных фактов рождения и «смерти» частиц вещества. Но ценность волнового описания состоит в том, что соответствующая теория хорошо развита и инвариантна (безразлична) к природе того, что волнуется или колеблется. Именно эта инвариантность вселяет оптимизм относительно корректности выбранного способа описания Мира. Следует еще раз подчеркнуть, что в этом направлении трудилось очень много талантливых и просто гениальных людей. Поэтому когда в тексте используется слово автор, то это автор текста. Авторство голографической модели не определено и неопределимо.

С волнами, по крайней мере на поверхности воды, знакомы все. Это обьщенность, мимо которой проходят, несмотря на напоминание Козьмы Пруткова: «Бросая камушки в воду, наблюдай за кругами, ими образуемыми, иначе такое времяпровождение будет пустым занятием». За этой шуткой кроется глубочайший смысл зримой красоты и сокровенного разнообразия механизмов явления. Бегут волны. А что бежит? Вода как бьша, так и осталась на месте, чуть поколебавшись, потоптавшись. Возмутилась и успокоилась. Бежит возмущение. Но ведь видно, что бежит. Возмущение. Но может такого наделать. Смыть, снести, разбить о скалы. Значит, переносит энергию — возможность что-то совершить. В школе объяснят, что волны на воде есть результат проявления сил тяготения и поверхностного натяжения, да еще инерционных свойств самой воды. И будут правы. Этого вполне достаточно для корректного описания. Правда, если опустить в воду ухо, то при ударе камушка по поверхности воды можно услышать звук. Тоже волны. На этом описание можно закончить. На самом деле рано. Взаимодействие между частицами воды имеет электромагнитную природу, и поэтому исключать электромагнитные волны нельзя. Но все три типа волн не имеют никакого отношения друг к другу? Звук быстро затихает. В каком диапазоне измерять электромагнитные волны, никто не знает. К. Прутков, конечно, шутил.

Волны описываются простым по виду уравнением для амплитуды возмущений:

t — момент времени, в который наблюдается волна;

Д)И ^0 — величины, определяемые (или задаваемые) при t = о и г = 0;

i — мнимая единица;

(У — периодичность изменения волны во времени;

^ — ритм волны, т. е. повторяемость ее в пространстве.

Очень часто при введении комплексной функции оговариваются, что иметь дело с экспонентой гораздо удобнее с точки зрения математики, поскольку ее вид не изменяется при дифференциальных преобразованиях. Дело, однако, не в простом удобстве, а имеет гораз-

Время мнимо и доступно липп> приборам — часам. Точно так же и вещество вещественно в том смысле, что доступно прямому ощущению. Поле непосредственно можно лшпь мнить, но можно и измерять приборами. Это с)ацественное свойство мнимой части комплексной сущности. Ее с помощью преобразований, в данном случае с участием приборов, можно сделать доступной чувственному восприятию — овеществрпъ. Но косвенным образом. Геометрически это означает, что оси, которым принадлежат компоненты любой из названных пар, ортогональны и проекция любого однородного события (вдоль «оси» времени или, наоборот, вдоль «оси» пространства) на другую «ось» всегда равна нулю.

Для Поля вещество — лишь забавная игра его собственной структуры, иллюзия. Но для нас вещество вещественно. И в большинстве случаев можно обойтись без представлений о Поле. Как в доброй старой механике. Но и это иллюзия, граничащая с самообманом, поскольку Поле там скрыто за каноническими формами законов. Позже мы вернемся к существенно полевым понятиям классической механики, а теперь посмотрим на еще одну геометрическую особенность мнимых осей. Проективная геометрия утверждает, что мнимая ось есть ось замкнутая. То есть, по сути, это «ось» в виде кольца. Может, и очень деформированного, но «замкнутого». Отсюда немедленно следует целая череда известных физических фактов: магнитные поля токов имеют замкнутые силовые линии, а сами токи — замкнутые электрические цепи. Пока не повернещь выключатель, ток не течет и лампа не светит. Здесь ток в смысле движения заряженных частиц вещества. Но и меняющееся магнитное поле (магнитный поток) порождает замкнутое (мнимое) вихревое электрическое поле. Это в электродинамике, где все рассуждения построены на представлениях Поля. Здесь вещество вроде бы как чужеродно и «протаскивается» в феноменологию Максвелла в форме материальных уравнений.

В отношении иных диалектических категорий замкнутость мнимых осей приводит также к интересным следствиям, уже не столь изученным. Если время мни-

Нас интересует, что происходит при взаимодействии волн и каким образом из них могут возникать стационарные пространственно-ограниченные структуры, которые имеют свойства частиц вещества. Сложение (суперпозиция, интерференция) волн составляет предмет обширного отдела в физике. Рассмотрено невероятно большое число частных случаев. Как правило, это очень сложные в математическом отношении задачи. Но машинная математика чрезвычайно расширяет возможности анализа. Впрочем, мы рассмотрим достаточно простые упражнения.

Возьмем для начала «одномерную» интерференцию, то есть такую, когда волны бегут в одном или противоположных направлениях. В общем виде и эта задача достаточно сложна. Но есть один частный и весьма важный случай, реализующийся для волн с одинаковой амплитудой, одинаковой частотой и распространяющихся в противоположные стороны. Такую сгпуацию

Суммарная волна обладает чрезвычайно интересным свойством. Она никуда не бежит. Она пульсирует на месте, то есть, по существу, не зависит от координаты. Особенности стоячих волн детально разобраны во многих учебниках, и не имеет смысла повторяться.

Важность стоячих волн для нашего рассмотрения определяется тем, что они образуются достаточно часто. Практически всегда, когда есть полностью или частично замкнутая граничная поверхность. Это любое отдельное тело, например, человек или яблоко, либо полость в твердом или жидком веществе. Во всех этих случаях возникает не одна, а целый набор стоячих волн, который существенным образом зависит от геометрии и размеров ограниченного объема, а также и от свойств среды, его наполняющей. И вот здесь начинаются интересные вещи. Дело в том, что суперпозиция уже двух стоячих волн может образовать новую бегущую волну. Причем эта новая волна будет иметь уже не синусоидальную форму, но не это важно. Скорость распространения новой волны не «соответствует» скорости распространения. Она может находиться во всем диапазоне, от нуля (ведь стоячая — она потому и стоячая, что скорость распространения равна нулю) до максимальной. То есть электромагнитные волны, например, могут распространяться не только со световой, но и с «черепашьей» скоростью. Здесь, вероятно, следует читателя, неудовлетворенного логикой повествования, отослать к учебникам. Но вот графические примеры.

На рисунке показано, что для стоячих волн с близкими частотами (рис. а) скорость перемещения «суперпозиции» гораздо меньше, чем для волн с большей разницей частот. Следует оговориться, что все это верно лишь для не слишком различающихся частот, почти совпадающих длин волн.

В этом упражнении за «амплитуду» стоячих волн бьша выбрана их «длина». Но, в принципе, мы можем оперировать и временной амплитудой, и, если ©j ~ то ~ 2Ар,sin (cot) (cos (-k,x) + cos (-lc2x))

Отсюда для не слишком различающихся длин стоячих волн (Ц – к, —>^0 или Ак —> 0) вдруг получаем v = щ/Ак —>■ 00. То есть при суперпозиции двух стоячих волн мы получаем не одно физическое явление (волна с «черепашьей» скоростью), но и процесс с очень большой скоростью распространения.

В теории волн это хорошо известно, и «медленная волна» распространяется с «групповой» скоростью, а «быстрая» — с «фазовой». Известно также, что за перенос энергии «ответственна» групповая скорость, а фазовая компонента волны энергию не переносит. Важно подчеркнуть, что обе эти волны всегда сопряжены и, в полном соответствии с математикой, инвариантом скорости может быть лишь произведение групповой и фазовой скоростей:

Отсюда проистекает некорректность постулата о постоянстве скорости света. Он верен лишь для очень частного, хотя и важного, случая, когда

Эта некорректность «тащит» за собой целый ворох последствий явно негативного в гносеологическом смысле оттенка. На самом деле мы в любом случае имеем два сопряженных процесса, что очень характерно для комплексного числа. И скорость света

Следует особо подчеркнуть, что скорость любых волн (электромагнитных и механических, звуковых в том числе) всегда определяется как квадратичная функция. То есть мы всегда имеем дело с двумя скоростями, которые иногда совпадают.

Очень важный момент гносеологического смысла заключен в определении скорости света через электрические и магнитные свойства пространства. Иногда можно этим обстоятельством пренебречь и в системе измерений физических величин по Гауссу = 1.

Это характеристики так называемого пустого пространства — вакуума, что заставляет сильно усомниться в его «пустоте». Действительно, наличие физических сред (вода, стекло и т. п.) меняет эти постоянные, причем иногда очень значительно, и с’ = 1 / (е^ец^р), где 8 и р — характеристики среды.

В гауссовой системе и р^ отсутствуют и скорость света зависит только от свойств среды е и р. Поразмыслив далее, мы должны прийти к вьшоду, что вакуум вовсе не пуст, обладая электрическими и магнитными свойствами.

Вернемся к понятийной подмене, о которой упоминалось ранее. Макс Планк для объяснения излучательной способности «черного» тела предположрш, что излучение и поглощение электромагнитной энергии происходит определенными порциями — квантами Е = hv, здесь Е — квант энергии, зависящий от частоты света — V, а h — постоянная Планка. Далее произошло то, что должно бьшо случиться во времена статистических вероятностных представлений, рожденных трудностями термодинамики. Энергия в теории теплоты никуда не исчезает (сохраняется) и аддитивна, т. е. ее можно складывать. Теперь легкая подмена: не поглощение (излучение) осуществляется дискретными порциями энергии, а сам свет состоит из квантов энергии — фотонов. Не очень понятно, как такое представление могло сложиться и прижиться. Ведь в опытах по интерференции света уже давно было известно, что при сложении волн с одинаковыми фазами и амплитудами интенсивность не удваивается, а учетверяется, что соответствует простым соображениям: энергия (либо интенсивность) есть квадратичная функция напряженности поля

А теперь «почувствуем» разницу фотонного и классического мировоззрения. Пусть в данной области пространства «бежит» невообразимо большое число волн различного направления, различных частот и фаз. Но очень много. Тогда позитивистский фотонный подход дает просто бесконечную плотность энергии. Такую ничем не удержать. Взрыв. Известная в конце девятнадцатого века «ультрафиолетовая катастрофа». В классической волновой теории все гораздо спокойней. Если волн очень много, то любой волне, бегущей в данном направлении, отыщется точно такая же, но бегущая в противоположную сторону. Образуется стоячая волна, которая энергию никуда не переносит. Уже легче. Далее. Каждой волне с данной частотой и данной фазой отыщется другая с той же частотой, но противоположной фазой. И результирующая их интенсивность (энергия), оказывается, вообще не существует для нас. Даже если волн много и потому именно, что волн много. Но для нас это и есть вакуум. Так, отдельные всполохи света непонятной природы, вследствие того, что волны там «живые». Бегут, изменяются. Меняются фазы, и иногда это становится доступным наблюдателю как случайные вспышки света.

Пустота на самом деле — это плотная ткань не видимого для нас света. Но не только его, как будет показано в следующем параграфе.

А теперь сделаем некоторые выводы.

Первое. Если отыщется такой умник, что умудрится «срезать» — детектировать одну из компонент «черного» излучения Пустоты, то он будет в состоянии либо произвести кощмарную катастрофу, либо создать новую Вселенную.

Второе. Как поучал К. Прутков относительно волн на воде, то стоит прислущаться. Камень упал в воду. Круги побежали. Довольно медленно. Но ведь что произошло, когда камень упал в воду? Связи между частицами имеют электрическую и магнитную природу. Их (связей) нарушение (движение зарядов) приводит к генерации электромагнитных волн. Отражаясь от различных препятствий и неоднородностей, они формируют систему стоячих волн, которых много. В результате образ)чотся «медленные» волны. Их легко услышать, опустив голову в воду. Шлепок камня по воде сопровождается звон-

Теперь еще одно важное замечание относительно природы волн и полей. Юзассические рещения в виде уравнений волны следуют из дифференциального уравнения второго порядка. Это немедленно приводит к очень интересному результату. Искомое решение описывает не одну, а две одинаковые волны, распространяющиеся в противоположные стороны. В общем случае это две сферические волны, одна из которых «бежит» из центра рассматриваемой области поля, а вторая — к центру. То есть, по существу, решением волнового уравнения является стоячая волна. И требуется задание неких начальных или граничных условий, чтобы из стоячей волны получить бегущую. Например, поставить с одной стороны зеркало, как мы делали, чтобы получить стоячую волну. Или еще что-нибудь придумать. Но в электродинамике поступают просто: получив сумму решений, одно из них «забывают» и рассматривают лишь бегущую волну. Иногда, правда, решая волновое уравнение для потенциалов поля и, получив два типа волн в виде запаздывающих и опережающих, приводят достаточно весомое оправдание тому, что один тип отбрасывается. Опережающие волны противоречат принципу причинности. Следствие не может опережать причину. И это просто обывательский взгляд на детерминизм. Хотя повседневный опыт показывает, что следствию всегда предшествует причина, но логически это ниоткуда не следует.

Впрочем, если бы мы имели дело только с «бегущими» решениями волновых уравнений, то все равно получили бы стационарные структуры поля, которые имеют свойства частиц. Или проточастиц. Это не так уж важно.

А = A^cos{(ot – к +Фо)

которое в большинстве случаев является частным случаем более общей комплексной функции

А =

Используемые здесь обозначения общеприняты:

? — координата, в которой наблюдается волна;

ДО более глубокий смысл, если вспомнить о принципиальной комплексности окружающей нас реальности, выраженной множеством «сдвоенных» понятий: пространство и время, вещество и поле, бытие и сознание, жизнь и смерть… Действительно, пространство пояти вещественно, его, по крайней мере, можно зримо ощутить, если, опять же, глазу есть за что зацепиться. За некие вещественные ориентиры.

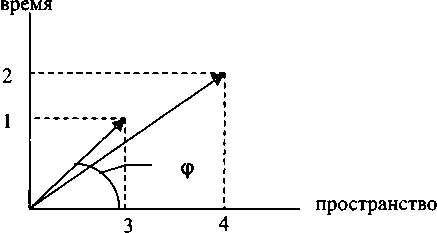
Рис. 2.5.1. Координаты «пространство — время»

Например, совершая какие-либо манипуляции со временем на отрезке между точками 1 и 2, мы всегда

имеем нулевую проекцию этого события. Точно так же и проекция отрезка 3—4 на ось времени всегда равна нулю. Однако задание числа в виде

Z = 3 + il

или

Z = 3 + i2

приобретает вполне прозрачные смысл и значение. Мы можем судить о величине, например, вектора (3, 1) и о некоторой скорости. Величину можно определить по теореме Пифагора:

г^ = П + 32,

а «скорость» как функцию угла поворота: v = ctg ф. Мнимая единица i в записи комплексного числа Z = а + ib

означает попросту, что а и Ь принадлежат осям, повернутым относительно друг друга на девяносто градусов. То есть оси, вообще-то, равноценны в своем значении. Можно, конечно, поместить себя в «нулевую» точку пространства, не имеющую протяженности, и в этом случае течение времени потеряет для субъекта смысл. Но для этого необходимо великое искусство. Так говорят йоги. Во всех остальных случаях адекватное определение реальности требует именно комплексного знания. Отсюда известное: memento mori. Живущий не имеет права забывать о смерти, хотя для него она мнима. Там, за чертой, полнейшая неопределенность. Некая отвлеченность. И невежды полагают, что переход за черту может избавить их от всех земных проблем. Но с точки зрения «потустороннего» мира жизнь столь же мнима, как и смерть для живущего в мире этом. Иллюзия. И «рождаться», наверно, так же неприятно, как и умирать. Может, поэтому кричат

И плачут младенцы, едва успев сделать первый вдох. Плачут, пока не смирятся. О чем это я? Да о том, что в пространстве — времени мнимым представляется не время, а пространство.

МО, то «ось» его замкнута. Впрочем, цикличность времени хорошо известна на уровне не научного, но обыденного сознания. Солнце всходит и заходит. Сменяют друг друга года. Но из равноценности пространства и времени следует и замкнутость пространства. Разница лишь в кривизне (размерах) соответствующих «осей-колец». Подобие Поля и Пространства внушает сомнения в том, что это разные вещи. И у автора нет других идей. Трансформации полей в виде индуцированных вихревых структур есть не что иное, как преобразование пространства во время и, наоборот, времени в пространство. Если говорить о замкнутости и цикличности жизни и смерти, то это, вероятно, относится к вопросу о реинкарнации и т. п. Вернемся к волнам.

ДОВОЛЬНО легко создать, если на пути распространения волны поставить зеркало. Тогда падающая и отраженная волны и удовлетворят обозначенным условиям.

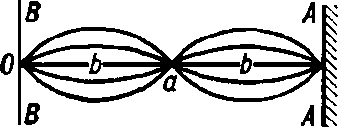
Рис. 2.5.2. Стоячая волна

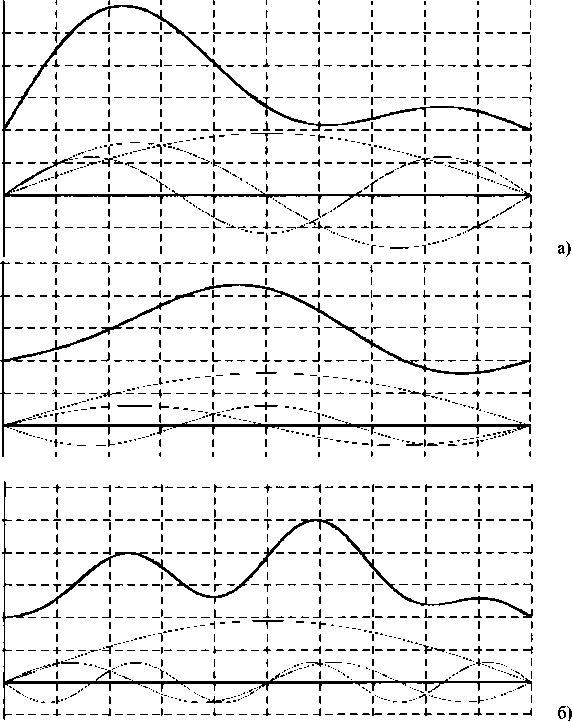
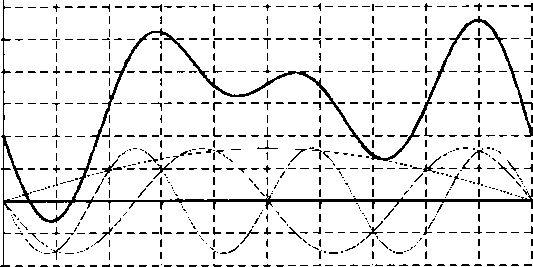
Рис. 2.5.3. Бегущие волны, порождаемые суперпозицией

стоячих

2Ap,sin (cot) 2cos (x (Ц- к,) / 2) cos (x (kj+ k,) / 2).

= V X V.. гр ф

V = V..

гр ф

где вц и Рр — это электрическая и магнитная характеристики пространства, в котором происходит распространение волны.

Но в не очень «физичной» системе интернациональных измерений (СИ):

£q = 8,85 X 10 ‘^ Фарад на метр, а Цд = 4я X 10 ’ Генри на метр.

J~E^

(здесь Е — напряженность поля), поэтому при указанном типе интерференции:

1~(2Е)^,

но не J ~ 2J. = + Е^, что вытекает из фотонного пред

ставления света или электромагнитного поля J =

Более того, в случае «фотонов» с противоположными фазами мы получали бы вновь суммарную (удвоенную в данном опыте) энергию. Но в классической волновой теории мы должны вначале определить результирующую напряженность (как геометрическую сумму векторов) и лишь затем вычислить квадрат. Так вот для волн с противоположными фазами мы получаем просто «отсутствие» энергии. И это очень примечательный момент. Волны (поля) никуда не исчезли. Они как бьши, так и остались, но для нас не существуют (в той области пространства, где происходит сложение волн в противофазе, наш экранчик не освещается).

КИМ звуком, распространяющимся со скоростью полтора километра в секунду. И только затем интерференция звуковых волн создает эффект механических, разбегающихся по воде кругов. Впрочем, рядом с упавшим камнем это и не круги вовсе.

ЧАСТИЦЫ

Рассмотрим более сложный, нежели в предыдущем параграфе, случай интерференции волн. Пусть две одинаковые волны распространяются не вдоль одной оси, а пересекаются. Это тоже довольно легко смоделировать в эксперименте. Теперь потребуется уже два зеркала.

В результате получим «двумерную» интерференцию двух одинаковых волн. Допустим, что исходная волна не меняет поляризации и пусть вектор электрической напряженности все время находится в плоскости рисзшка.

То есть в результате взаимодействия двух «бегущих» волн образовалось нечто вращающееся, но ьшкуда не бегущее. Что вполне соответствует определению «стационарный объект». Мы и на самом деле имеем здесь нечто подобное частице или проточастице. Впрочем, не только здесь, но и возле каждого из зеркал. Вблизи отражающих поверхностей происходят удивительные вещи.

Если продолжить анализ свойств объекта, образовавшегося при взаимодействии двух волн, по использованной выше графике, то непременно впадем в ересь. Дело в том, что якобы наглядное изображение волны в приведенном виде имеет очень малое отношение к реальности. Решения волнового уравнения в виде А = A^sin (©t – кг + (рд)

Впрочем, и искать незачем. Традиционная схема манипуляций в электродинамике имеет следуюпщй вид. Берут уравнения Максвелла в отсутствие токов и зарядов:

rot Е =

rot Н = .

Затем конструируют из них уравнения второго порядка отдельно для каждого из векторов £ и Н и получают волновые уравнения Даламбера:

rotrotE + ^^ = 0 dt^

Если развить предложенную графику до «волнового решения», то получим систему «сцепленных» экваториальных торов, не очень похожую на картину классического сферического волнового фронта. Именно о бесконечной «сцепке» вихрей торов и рассуждал Максвелл в своей теории. Но потом это приобрело статус «снисходительной наивности».

Замкнутые силовые линии поля, то есть такие линии, касательные к которым (векторы Е или Н) одинаковы по длине, в соответствии с проективной геометрией являются мнимыми осями. Поэтому электромагнитное поле хотя и «принадлежит» трехмерному пространству, но является объектом многомерным, имея, по крайней мере, пять осей. И, вероятно, исследовать поле удобнее с помощью методов неевклидовой геометрии. Очень изящный подход, к результатам которого мы обратимся чуть позже, развит минералогом С. В. Рудневым.

Но вернемся к нашему опыту с двумя зеркалами. Теперь ясно, что рассматривать поле в точке пересечения лучей, соответствующих направлетшям распространетшя поля, вообще некорректно. Следует рассматривать, по крайней мере, область с размерами порядка длины юлны поля. Но интуитивно результат уже ясен. В области пересечетшя юлн мы получим статщонарную вихревую структуру поля. Вокруг вращающегося в плоскости рисунка вектора электрической напряженности поля «вращается» вихрь векторов магнитной напряжеьшости. Кроме того, он «кувыркается» вместе с вектором электрической напряженности.

В результате этого незатейливого движения силовые линии магнитного поля описывают сферические поверхности. Но и определение электрического поля с помощью вектора тоже не вполне корректно. На самом деле из уравнений Максвелла следует, что электрическое поле представляет собой совокупность вихрей вокруг вихря магнитной компоненты.

Тем самым мы подошли к той замечательной интерпретации пятимерного аналога евклидовой плоскости, которую выполнил С. В. Руднев. Не вдаваясь в математические подробности, отметим, что четырехмерный аналог евклидовой плоскости известен достаточно давно под названием «прямой круговой цилиндр Клиффорда». Можно под многомерностью понимать нечто совершенно фантастическое, трансцендентное и не доступное человеку среднего ума. Но никакого запредельного смысла в многомерности нет. Это, конечно, авторская точка зрения. Дело в том, что если, например, описывать движение точки по поверхности обычного цилиндра с помощью задания обычных трехмерных координат, то запись соотношений между ними и составляет не то чтобы запредельную, но достаточно трудную задачу. В формулах будут постоянно «путаться» квадратичные величины и корни, часть из них, определяющие саму поверхность. Очень громоздкая запись.

Но если выбрать на поверхности цилиндра замкнутую линию минимальной длины (в данном случае — окружность) и «назначить» ее координатной осью, то запись положения точки на поверхности сводится просто к заданию четырех чисел. «Движение» точки по поверхности будет описываться простыми соотношениями, подобными тем, что используются для описания движения на обычной плоскости. Поэтому «четырехмерный» цилиндр Клиффорда и является аналогом евклидовой плоскости. Те законы, которые справедливы для плоскости, выполняются и на поверхности цилиндра Клиффорда. По сути, это обычный цилиндр трехмерного пространства. Возможно, в этом месте текста многим геометрам захочется проломить автору голову, но я все же склоняюсь к мысли, что четвертая ось здесь введена для удобства.

Прямой круговой цилиндр — вещь достаточно абстрактная. Он обладает бесконечной длиной. «Начинается» в бесконечности и «там же» заканчивается. Это не очень характерно для реальности. Поэтому прагматический смысл введения пятой оси очень значителен. Грубо говоря, С. В. Руднев свернул цилиндр Клиффорда в бублик — экваториальный тор. В результате на новой поверхности появилась еще одна замкнутая линия минимальной длины, которую можно использовать в качестве оси. Вот теперь появилась конструкция, вполне ограниченная своей поверхностью в трехмерном пространстве и, что очень важно, позволяющая на этой поверхности использовать законы евклидовой плоскости.

Конечно, изложенная интерпретация очень груба и утрирована. На самом деле все гораздо сложнее и тоньше, но здесь важны, скорее, выводы из работы Руднева. Их множество, но реальность такова, что все мыслимые формы этого мира тяготеют к формам тора. И позже мы вернемся к этому.

Оказывается, что в соответствии с геометрией рима- новых пространств всякому экваториальному тору соответствует (читай, есть) свой полярный тор.

А еще у него есть шесть сопряженных торов-спутников. И пересечения характеристических (геодезических) линий этой торовой системы дают структуры из точек, очень похожие на реальные кристаллы. Ограниченные (и ограненные) в пространстве и заведомо «дефектные». То есть обладающие структурой, не соответствующей идеальному порядку классической кристаллографии. И это очень красивый результат, полученный Рудневым на поприще применения к описанию реального вещества методов неевклидовой геометрии.

Графика уравнений Максвелла оказывается очень похожей на геометрию тора. Может показаться, что мы имеем альтернативные способы описания реальности. Но скорее это просто дополняющие друг друга приемы, еще раз напоминающие о древней сентенции: «Пустота имеет природу Света, а Свет — природу Пустоты». Здесь подчеркнута не только неразрывность (нерасторжимость) этих категорий, но и то, что каждая из них не исчерпывает другую. И методы, наработанные в теории колебаний, могут сослужить вполне исправную службу.

В нашем опыте с двумя зеркалами мы «заставили» интерферировать волну саму с собой. А что будет, если волны разные? Ответ известен давно. Стационарные структуры колебаний возникают только в том случае, если частоты составляющих процессов равны или кратны друг другу. В рассматриваемом примере равенство (автоматическое) частот приводит к образованию кольцевых или эллиптических структур. В остальных случаях это более сложные структуры. Впервые эти формы стационарных колебаний в механике исследовал Лисса- жу, по имени которого они и называются.

Очень интересно наблюдать их образование на экране осциллографа при наличии перестраиваемых генераторов частоты. Ныне, к сожалению, осциллограф — довольно редкий прибор в школе. Разнообразие фигур Лиссажу чрезвычайно. От кольца, вырождающегося в отрезок прямой лини, до затейливых многопетлевых структур и сеток.

Еще одно интересное свойство фигур Лиссажу можно также наблюдать на экране осциллографа, если один из генераторов может изменять не толыю частоту, но и фазу шлебаний. При изменении фазы картинка нач1шает как бы вращаться. На самом деле это просто ее деформация, но создается ощущение, что мы наблюдаем плоскую проекцию вращающейся фигуры. И это тоже не фокус. Реальные повороты определяются изменением фаз. То есть есть два принципиальных типа движения, из шгорых «конструируются» все остальные. Перенос и вращение зависят от изменений частотных и фазовых соотнощений.

Фигуры Лиссажу можно смоделировать и на экране компьютера. Здесь можно изобразить даже интерференцию трех взаимно перпендикулярных волн. Принципиально «трехмерная» интерференция отличается от «двумерной» только еще больщим разнообразием форм, поскольку уже и в «двумерном» случае (для электромагнитных волн) мы имеем дело с объемными структурами.

На экране осциллографа в случае «двумерной» интерференции и на мониторе шмпьютера для кратных по частоте «волн» мы получаем совершенно дискретные (отдельные) структуры, которые уже не зависят от координат (стоят на месте) и от времени, хотя о пульсациях и можно говорить. Но чтобы быть уверенными в том, что мы имеем дело с частицами, следует определиться, откуда берутся такие характеристики, как заряд и масса. По Максвеллу, плотность заряда определяется как дивергенция (расхождение) электричесшй напряженности поля. То есть если внутри некоторого объема V имеем заряд, то через поверхность, ограничивающую этот объем, поток вектора электричеоюй напряженности отличен от нуля

Пусть в случае «двумерной» интерференции (опыт с двумя зеркалами) мы можем записать для точки пересечения электрическую компоненту исходной волны в виде Е| = E^jSin (ot – кх + фц),

Это означает, что для поперечных волн изменений напряженности поля вдоль вектора распространения не существует. То же самое следует констатировать и для второй волны, и закрыть вопрос о заряде, поскольку его вроде бы не возникло, т. е.

Чтобы показать, что это не так, допустим, что условия нашего опыта таковы, что разность фаз Лф равна 2тт, где п — целые числа: 0,1 и т. д. Тогда это слагаемое в фазе можно опустить, и мы видим, что обе напряженности, Е| и Е^, меняются по одному закону:

То есть волне, распространяющейся вдоль оси х, можно сопоставить и колебания напряженности вдоль нее. То же самое и для волны, распространяющейся вдоль оси 7. Отсюда следует и гораздо более общий вывод, что для волн с непараллельными волновыми векторами к практически всегда существ)чот продольные компоненты. Особенно очевидно это для волн совпадающих или кратных частот.

Выполнив вышеобозначенную подтасовку компонент поля и применяя оператор div, получим: div (Ej + Е^) = Egk (cos (cot – кх + фд) + cos (cot – ky + ф^ + 2тт)).

Преобразуем сумму косинусов в произведение (cos А + cos В = 2cos ((А + В) / 2) X cos ((А – В) /2)):

Последний сомножитель дает при четных п плюс единицу и при нечетных — минус единицу. Поскольку X = ct и у = ct, а опыт мы проводим в вакууме, где отсутствует дисперсия и дк ! дсо = О, и волновой вектор можно заменить волновым числом, то к = 2я/А, = су/с, то и в первом косинусе аргумент сводится для нашего простого случая к (ср^ + тт) и div (Ej + Е^) = 2E^k х cos (срц + тт) X cos (тт) = 2Ецк х cos (ср^,).

Поскольку последнее выражение 2E^k х cos (ср,,) = 4яр, то, интегрируя его по объему с радиусом X / 2, и т. к. к = 2я / X, получим:

Q = -TiX EqCos^o. 6

Последнее выражение явно не всегда равно нулю. Отметим несколько особенностей в нашем упражнении. Вычислять заряд при п = О вообще не имеет смысла, поскольку, с одной стороны, такой опыт невозможно осу- ществрпъ, а с другой — аналитически мы тоже получаем нулевую плотность заряда. Случай с п = 1 можно реализовать и на одном зеркале, подразумевая, что мы имеем дело не с бесконечно узким лучом, а с целым «пучком» лучей, имеющим поперечное сечение порядка длины волны. Тогда при углах падения ~ 45° мы получим тот же результат, что и с двумя зеркалами, но вблизи поверхности. Поэтому отражающие поверхности вблизи себя образуют плотное облако виртуальных зарядов и обладают, вероятно, магическими особенностями.

Далее, наличие в последнем выражении тригонометрической функции cos (фц), а в более общем случае зависящей от разности фаз, означает, что суммарный вектор (Е, + Ej) может вращаться вокруг точки пересечения и в плоскости чертежа либо по часовой стрелке, либо против. Вокруг чего он вращается, мы еще не знаем, но можно предположить, что именно с направлением вращения связан знак заряда. Возможно, следует еще обратить внимание на наличие в знаменателе выражения для заряда числа «три», возникающего за счет определения объема сферы 4тп^/ 3. Это интересно в связи с экспериментально-теоретическими наблюдениями структур с дробным зарядом — кварков.

К другим характеристикам образующихся интерференционных структур, таких как масса, мы обратимся чуть позже, а пока рассмотрим практическую целесообразность приведенного рассмотрения, в том смысле, что встречаемся с этими эффектами повседневно.

ГОЛОГРАФИЯ И ФОТОГРАФИЯ

Очень часто встречается подмена понятий в определении терминов. Например, первый корень в слове «голография» (holos) иногда интерпретируется как «объемный», имея в виду, что голограмма дает объемные

Обратимся к технической стороне вопроса. Голограммы «записывают» с помощью обычной фотоэмульсии, нанесенной на достаточно жесткую подложку. На обычной фотопленке или фотобумаге тоже можно записать голограмму, но из-за неизбежных деформаций голограммы восстановленное изображение будет искажено до неузнаваемости. В качестве подложки используют, как правило, стеклянные пластины. На фотоэмульсию направляют два световых потока: опорный и предметный. В качестве первого используется часть света источника, а второго — свет источника, рассеянный (отраженный) объектом, голограмму которого и хотят получитъ.

Теория голографического процесса развивалась чуть ли не параллельно с историей фотографии. Но для ее реализации на практике не хватало качественных источников света. Дело в том, что для регистрации голограммы нужен достаточно упорядоченный (когерентный) свет с хорошей интенсивностью. Источники такого света появились не очень давно — в начале шестидесятых годов двадцатого века. Это лазеры. С их появлением техническая голография испытала бум своего развития. Появилась и художественная голография, о которой, вероятно, слышали почти все.

После экспозиции и проявления фотопластинки можно «на глаз» определить, что она засвечена, и лишь иногда видны пятна с разной степенью потемнения, разводы и структуры, напоминающие перистые облака. Никакого изображения предмета не наблюдается. И это естественно.

Но если фотопластинку с голограммой вернуть на место в схеме регистрации, а светоделительную пластинку заменить качественным зеркалом, то там, где раньше был регистрируемый объект, можно наблюдать действительно объемное изображение. Причем это мнимое изображение.

Действительное изображение восстанавливается в свете проходящих лучей и выглядит не очень узнаваемо. Рисунок 2.7.2.

Обычно наблюдают именно мнимое изображение, названное так потому, что реального светового потока от него нет. С реальным изображением дело обстоит сложнее, ибо то, что здесь наблюдается, есть реальная структура из прошедшего света.

3 — голограмма; 4 — наблюдатель; 5 — мнимое изображение; 6 — действительное изображение.

Реальные схемы получения голограмм, конечно, более сложны, чем приведенная, но не это для нас важно. Рассмотрим область пересечения опорного и предметного световых потоков. И здесь мы можем вспомнить наш опыт с двумя зеркалами. Области пересечения световых потоков в обоих случаях мало отличаются. Конечно, наш опыт — рядовая идеализация, но ее результаты можно перенести и на случай практической голографии. В области пересечения образуется «рой» виртуальных частиц, обладаюш,их электрическим зарядом. Они очень разнообразны по структуре и свойствам и «живут» очень непродолжительное время. Если времена упорядоченности лазерного излучения весьма внушительны и достигают долей секунд, то время «упорядоченности» рассеянного объектом лазерного света не превышает време-

Что происходит далее? В течение 10 * секунд мы имеем вполне упорядоченную структуру из электрических зарядов в области фотоэмульсии. Эта структура вполне могла бы провзаимодействовать с реальным веществом эмульсии типично химическим образом. То есть образовалась бы структура, включающая в себя и виртуальные, и реальные частицы. И действительно характерные времена «химического» взаимодействия близки к длительности тепловых колебаний атомов, порядка 10’** с. В громоздких химических реакциях, где происходит многоэтапное действо перегруппировки атомов и их ансамблей, времена процесса могут составлять секунды и даже часы, но элементарные акты длятся в течение 10 ‘*с. То есть за время жизни виртуальных частиц они могут вступить во взаимодействие с реальным веществом до 100 тысяч раз. Процесс совершенно реален. Образуется новое химическое соединение с неоднородной структурой. И это необратимый процесс. При проявлении эмульсии мы отмываем «лишние», побочные продукты процесса, а оставляем серебро, которое после того, как его атомы покинули виртуальные подруги, остается в «элементарном» и малоподвижном состоянии, сохраняя память недолгой встречи. Если этих грустных меланхоликов вновь осветить тем же светом, то они «вспыхивают» мечтами о прошлом, и мы видим восстановленные изображения. Иллюзия.

Вспомним теперь рисунок из предыдущего параграфа о том, что происходит вблизи отражающей поверхности, и переместимся мысленно вглубь отражающей среды. Точно такую же картинку пересечений мы можем нарисовать для преломленных, прощедших и переотраженных лучей. Впрочем, здесь действует более сложный механизм рассеяния на структуре среды. Тем не менее, результат тот же. Образуются виртуальные частицы.

В электродинамике понятие «виртуальная частица» не используется. Говорят о поверхностных или объемных плазмонах. Суть одна. Виртуальный заряд «вторгается» в электронную (или, еще более обще, зарядовую) структуру и нарушает равновесное состояние. Темпераментные подвижные реальные частицы начинают суетиться, и некоторые даже выскакивают на поверхность. В этом состоит суть фотоэффекта. Не оттого электрон выпрыгивает, что ему придали достаточную энергию и он «отвязался», а потому, что оказался лишним в зарядовой структуре. Впрочем, в энергетическом смысле разницы нет. Разницы нет и в фотоэффектах при регистрации голограмм и получении фотоизображения. Разница в технике.

Рассмотрим схему фотографирования. Освещенный (неупорядоченным) светом объект рассеивает его по-прежнему каждым атомом поверхности в отдельности. Вот и построим схему получения изображения отдельного атома, который по-прежнему в течение примерно 10 * с излучает достаточно когерентный свет.

Рис. 2.7.3. Схема получения фотоизображения I — излучающий атом; 2 — объектив; 3 — фотопластинка.

На традиционной схеме мы вновь видим, что в области пересечения характерных лучей картина мало чем отлР1чается от рассмотренной ранее. И в эмульсии фотопластинки мы вновь получаем виртуальную частицу, которая может вступить в химическое взаимодействие с веществом эмульсии. Что и происходит. Далее можно достроить остальные рассеивающие свет частицы объекта и получить изображение его всего. Но состоит оно из отдельных изображений каждой молекулы и каждого атома поверхности объекта. Причем эти голографические изображения буквально повторяют те объекты, которые когерентно рассеивали свет. Поэтому фотография на самом деле обладает гораздо большей информацией, чем мы привыкли считать, чуть ли не ежедневно сталкиваясь с этим достижением современности.

Помимо интегральной картинки распределения амплитуд интенсивностей света, запечатлевщей некий образ, в фотографии содержится фазовая структура, которая помнит, из чего сделан объект, запечатленный на ней, как он пахнет и, наверное, как звучит в момент съемки. По фотографии можно изучать химический состав, причем не столь важно, с какого расстояния сделан снимок, потому что в эмульсии «действуют» те же частоты, что излучили сам атом или молекула. Вернее, не «те же самые частоты», а их соотношения, что для нас гораздо важнее. То есть соотношения между ортогональными составляющими частот. Может, следует здесь напомнить, что любые колебания можно разложить на три перпендикулярные составляющие, и сами частоты уже не имеют значения, поскольку для образования стационарной струюуры необходимы только либо совпадение частот, либо их кратность.

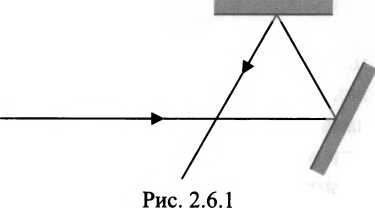
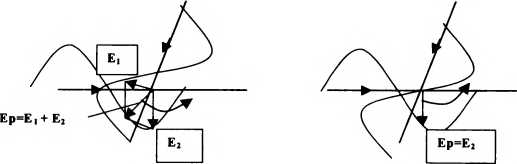
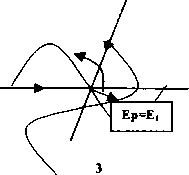
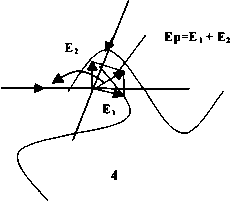
Рис. 2.6.2

Повторив рисунок для нескольких последовательных моментов времени и просуммировав каждый раз векторы пересекающихся волн, легко увидеть, что сумма векторов никуда не «бежит», а вращается вокруг «точки» пересечения.

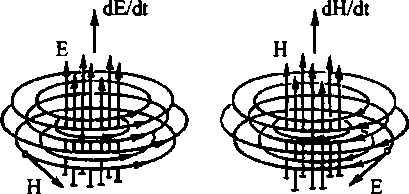
а) б)

Рис. 2.6.3. Вращение вектора электрической напряженности

или

Д — Д 0-i(kr-o)t-(po)

верны лишь для проекций, а восстановить «чертеж» по проекциям дело не простое. Тем более что «удобства для» при построении проекций отброшены некоторые «мелочи». В том числе и вторые (противоположные) решения. О чем идет речь? О том, что «противоположные» решения не устранимы волевым усилием. Чтобы понять их происхождение и значение, следует поискать другие виды решений волновых уравнений.

с dt

с dt

И

1

rotrotH + -V^ = 0.

дг

и вот, уже решая волновые уравнения, получают решения в указанном выше виде для каждой из проекций. Но исходные уравнения Максвелла тоже ведь решения и их «наглядность» гораздо вьппе, хотя их волновой характер и не вполне очевиден. Тем не менее «графика» уравнений Максвелла явно указует на их «волновую» природу: Рис. 2.6.4. (Кошкин и К“ с. 146)

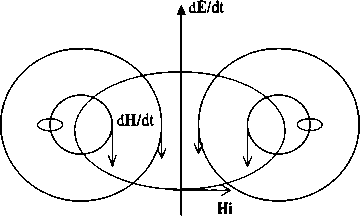
Рис. 2.6.5. К решению уравнений Даламбера

Структура поля без токов и зарядов на самом деле гораздо сложней и интересней, чем сложившееся современное представление. Именно оно, в отличие от максвелловского, является наивным.

Однако если спроектировать вихревую структуру на плоскость, то мы действительно получаем по два решения для каждой из компонент, а не только для веьсгора распро-

страненрш поля. Кольцо в проекции вырождается в отрезок и зеряет смысл дифференциального оператора rot, который указывает именно на то, что векторы на противоположных сторонах вихря имеют противоположные направления.

Е

Н

Н

Рис. 2.6.6. «Кувыркания» векторов электромагнитного поля в точке пересечения

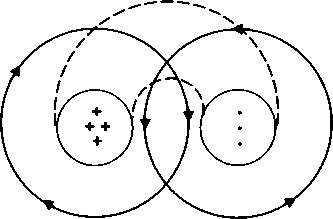
Рис. 2.6.7. Вихри Е и Н

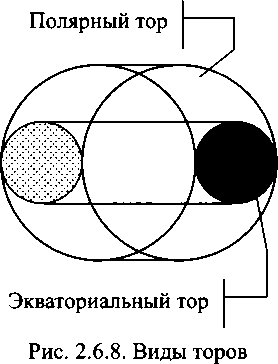
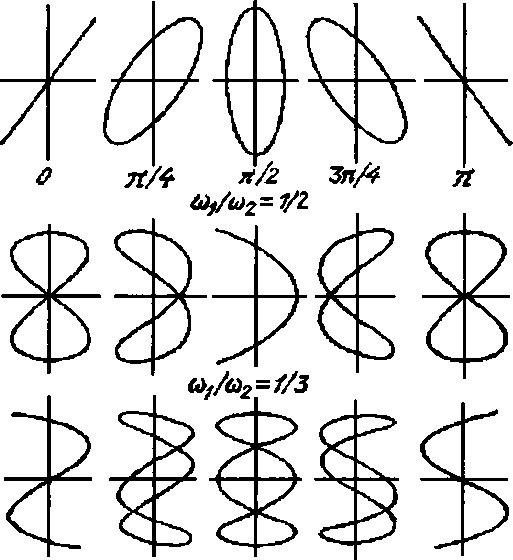
Рис. 2.6.9. Соотношение частот и фаз

Изменяя частоту одного из генераторов, легко видеть «разрушение» стационарных картинок с образованием бегзлцих по экрану волн. Затем, когда частоты генераторов вновь становятся кратными, на экране вновь возникает стационарная картинка, мало похожая на предьвдущую. Интересны моменты, кюгда частоты генераторов из кратных становятся «слегка» некратными. Вначале неподвижная прежде картинка начинает «плыть» по экрану. При большей расстройке от кратной частоты скорость убегания быстро увеличивается, и структура «распадается» в

бегущие волны. И это не просто фокусы радиотехнической схемы. Реальное движение реальных тел связано именно с частотными эффектами.

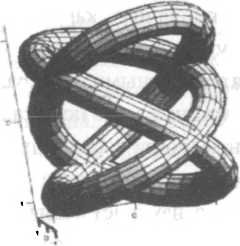
Рис. 2.6.10. Пример трехмерной интерференции

\Eds = 47r\pdV^0

S V

и, естественно, если зарядов нет (или число положительных равно числу отрицательных зарядов), то поток равен нулю, или в дифференциальной форме:

div Е = 0.

Оператор div означает следзтощее правило дифференцирования:

divE =

дЕ. дЕ дЕ, —- + —- + —- дх ду дг

если ось X совпадает с направлением распространения к. Далее для удобства отъюстируем (выставим) зеркала так, что пересекающая волна распространяется вдоль оси у, и Е2 = EpSin (cot – ку + фц+ Дф).

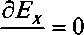
дх

разность фаз Дф накопилась на пути волны до пересечения с самой собой. Е| у нас описывает компоненту вектора по оси у, но зависит (в фазе) от дг-вой юдординаты, то есть является jc-компонентой волны. И, в полном соответствии с теорией для поля в отсутствие зарядов, мы получим

div (Е. + Е^) = 0.

Е = EpSin ((Ot – кх + фр).

div (Е, + Е^) = 2Ej,k х cos ((cot – кх – ку + срц+ 2тт) / 2) X cos (тт).

– Eq cos <Pq

(4пЛ
3 J	00

1

1 2

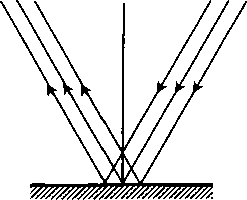
Рис. 2.6.11. Интерференция вблизи зеркала

восстановленные изображения. Но голос с греческого переводится как весь, полный. Конечно, в отношении изображения здесь уместно понятие «объемный», однако неизбежна и некоторая путаница. Впрочем, бог с ней. Ведь holos — это и звучащий голос, и, отсюда же, глаз — орган зрения, и glas — стекло, и глиссирующий, то есть скользящий, и т. д., и т. п.

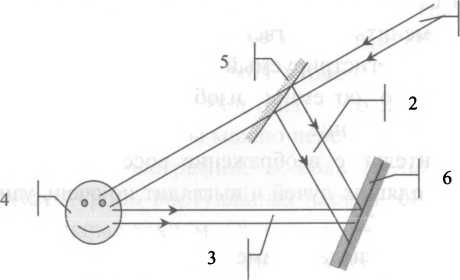
Рис. 2.7.1. Схема регистрации голограммы 1 — используемый световой поток; 2 — опорный поток;

3 — предметный поток; 4 — объект; 5 — светоделительная пластинка (прозрачное зеркало); 6 — фотопластинка.

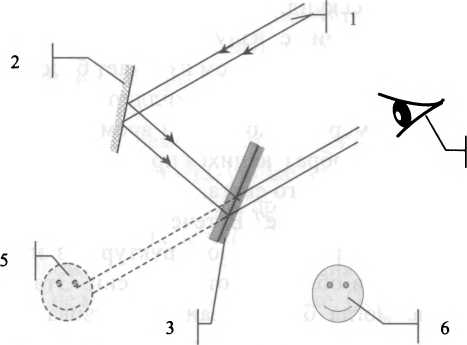
Рис. 2.7.2. Схема «восстановления» голограммы 1 — используемый световой поток; 2 — зеркало;

НИ порядка 10 * секунд. Дело в том, что рассеянный свет — это вторичное излучение атомов объекта. Каждого в отдельности. И атом излучает более-менее когерентно в течение одной стомиллионной доли секунды. Вот примерно таково же и время жизни виртуальных частиц, образующихся при взаимодействии опорного и предметного света.

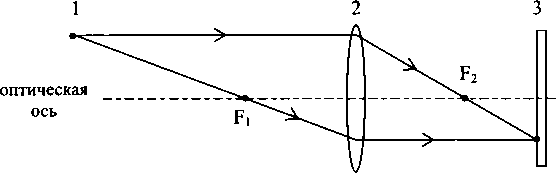
МЕХАНИКА ПОЛЯ

Заряд — не единственная характеристика частицы вещества. Более того, мы знаем, что существуют и частицы, не имеющие электрического заряда. Поэтому стоит вновь вернуться к описанию поля. По Максвеллу, для однозначного определения поля в «в точке» достаточно задания векторов его электрической и магнитной напряженностей. Собственно, поэтому прижилась устойчивая терминология — электромагнитное поле. В более позднем исследовании энергетического баланса электромагнитного поля Умов и Пойнтинг выяснили, что оно имеет механическую составляющую — переносит механический импульс. То есть следует говорить не об электромагнитном, но электромагнитно-механическом поле.

С механическими свойствами электромагнитного поля мы сталкиваемся в повседневном обиходе. В автомобильном генераторе взаимодействие механического и магнитного «факторов» возбуждает электрический. В любом практически электромоторчике «электричество», взаимодействуя с «магнетизмом», заставляет крутиться ротор. Наконец, движение зарядов (механическое) в электрическом поле порождает магнитное поле. Можно усомниться в корректности приведенных примеров и показать, что они не имеют никакого отношения к электромагнитному полю. Но это, что называется, «за деревьями леса не видно».

Если существует пара внутренне связанных векторов, то существует и их произведение. Например, векторы электрической и магнитной напряженностей поля в точке внутренне связаны зфавнениями Максвелла. Последние здесь, вообще-то, ни при чем, просто описывают характер связности. Просто электрический и магнитный векторы являются аспектами одного и того же эффекта и реализуются один в другом через некоторое движение действия. Чтобы как-то сгладить «заумь» сказанного, отошлем читателя к какому-нибудь учебнику по электродинамике. Там наверняка можно найти раздел о преобразовании этих векторов из одной инерциальной системы в другую. Если ввести параллельные и перпендикулярные составляющие векторов относительно относительной скорости V движения инерциальных систем, то можно записать

Н|| = Н,,; Н^=у

E^=E + -VxH, а H^=H–VxE. с с

=E + -VxH = 0, с

.. ЕхН

( 1

Е|| = Ец; Ej^ =у ^Ej^+-VxH ;

H^–VxE

С

здесь у = .Jl – v^/c^ и при v«c у ~ 1 и тогда

Эти выражения показывают реальную связь веиоров Е, Н и V, их внутреннюю однородность. Можно даже найти систему, движущуюся таким образом, что Е’ или Н’ будут равны нулю. То есть либо электрическое, либо магнитное поле будут отсутствовать. При этом

откуда относительная скорость движения инерциальной системы должна будет составить величину

• = c

  Для инерциальной системы, в которой магнитное поле

  Н’= О, ее скорость будет составлять величину

  ЕхН

• = c—

  Е^

  Однако одновременно обратить Е’ и Н’ в нуль нельзя, поскольку есть сохраняющаяся величина (инвариант) E^-ff = inv.

  Тем не менее, приведенные формулы создают ощущение, что и электрическое, и магнитное поля есть просто результаты некоторого движенрм — деформации пространства, и когда «вихрь скоростей» меняет направление, тогда мы и наблюдаем появление либо исчезновение поля. Что интересно, так это то, что именно в таком ключе — через введение поля скоростей в пространстве — Эйлеру удалось сделать значительный теоретический задел в теории сопротивления материалов (механика сплошных сред). Он отказался от рассмотрения структурных особенностей среды и предложил рассматривать физические тела как пространства с определенными свойствами. Это был очень плодотворный шаг, и Эйлер написал уравнения, по форме совпадающие с теми, какие спустя много лет использовал Максвелл. Одинаковость формы законов определенно указывает на тесное родство описываемых свойств. Можно назвать это, конечно, аналогией, но аналогия столь близка к тождеству.

  Имея в виду прозрачное понимание того, что описывает, а именно деформации, основные из которых линейные (сжатие — растяжение) и угловые (сдвиг), Эйлер составил дифференциальные уравнения:

  — = vrotcJ и — = vrotG,

  здесь G — напряжение сдвига; О — напряжение сжа- тия/растяжения; v — скорость звука в среде.

  В смысле аналогии можно заключить отсюда, что электромагнитное поле и есть проявление деформации пространства. Но чтобы аналогия бьыа более полной, сопоставим некоторые количественные характеристики. Плотность энергии электрического поля

3G ЬО ^

at at

1. р2

   Но плотность энергии при растяжении (сжатии) упругого тела выражается точно такой же формулой;

   1

W = -£oE ,

здесь Е—напряженность электрического поля; —электрическая постоянная, равная 8,85418782 х 10 ‘^ Ф/м.

W = ,

1. Е ,

   здесь Е — модуль Юнга, причем порядки чисел и ^ совпадают. Различие этих чисел возникает за счет того, что в среде электрическая постоянная домножается на относительную проницаемость, обычно большую, чем единица, а в случае механических деформаций относительная составляющая модуля Юнга может иметь значения меньше единицы.

   В механике сплошных сред совершенно прозрачна интерпретация силовых и энергетических характеристик через изменения пространственных, в то время как в теории электричества такой связи напрямую не просматривается. Закон Гука связывает относительную деформацию тела длиной 1 и сечением S с приложенной силой F и Е — механической постоянной (для данного материала):

   д1 _ F

   отношение F/S называют напряжением, и оно вполне аналогично электрической напряженности, «если пренебречь» зарядом. То же самое соотношение в виде

   д1х8 = —xFxl Е

   показывает, что потенциал Fxl соответствует изменению объема тела дУ = д1 х S. В общем, ничего, кроме геометрии с поправкой на свойства пространства (постоянная Юнга Е или электрическая постоянная при явном отсутствии вещества, т. е. для вакуума). Анализируя закон Гука, можно выявить целый ряд поучительных моментов.

   Напряженность поля (или напряжение деформации тела в механике) соответствует плотности силы, т. е. определяется как сила, действующая на единичную площадь — F/S. Это, по сути, не что иное, как давление, а если числитель и знаменатель домножить на длину 1, то F XI / (S X1) есть не что иное, как объемная плотность потенциала. Энергия деформации может быть определена как произведение силы на величину связанного с ней перемещения д1:

   здесь множитель 1/2 возникает при интегрировании силы: в начале деформации она мала (~0) и достигает значения F при конечном л1.

   Объемная плотность энергии

   опять выражается через геометрические характеристики. Надеюсь, читатель не слишком утомлен, чтобы почувствовать «геометрическую» природу всего и вся, что окружает его. И дело не в том, что все происходит в пространстве, а в том, что это происходит с самим пространством. Окружающий нас мир, вещи в нем и события — это в некотором смысле просто дефекты — деформации пространства. Пустоты.

   Можно воспользоваться рафинированной геометрией и показать, что механические и полевые эффекты есть лищь свойства пространства. По крайней мере, по общему виду соотношений и закономерностей.

T~ES’

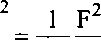
2ES^

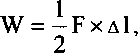
ГЕОМЕТРИЯ ПОЛЯ

Вернемся к формулам преобразования напряженностей поля при переходе от одной инерциальной системы к другой. Сами по себе преобразования Лоренца есть «чистой воды» геометрия. Точнее, с учетом того, что в них фигурируют не только координаты, но и скорости, — это геометродинамика.

Выражение вида

Fjj =eE + -VxH с

В этом выражении содержится ряд утверждений фундаментального характера:

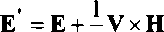
с

есть результат геометрическрк преобразований, но в виде

это фундаментальный экспериментальный результат, известный под названием силы Лоренца. Теперь, если обратиться к «чистой» геометрии, то же самое выражение мы обнаружим при описании свойств кривой линии в трехмерном пространстве. Какое дело нам до кривой в пространстве? Но силовые линии поля и есть кривые в пространстве. В теории поля их именуют линиями тока.

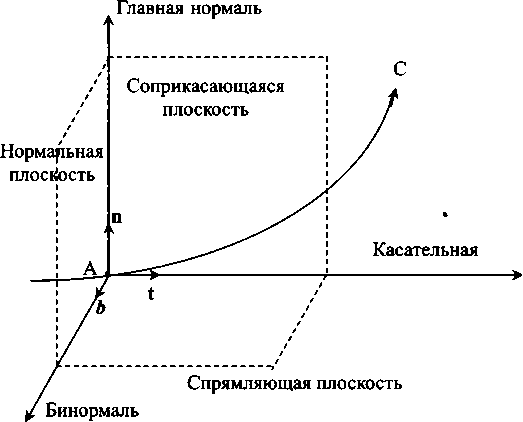
Рис. 2.9.1. Подвижный трехгранник Здесь t, п, Ь — векторы Френе: единичные векторы касательной, главной нормали и бинормали соответственно. Вектор касательной имеет смысл скорости движения точки А по кривой С, вектор главной нормали — центростремительного (к центру кривизны кри-

ВОЙ) ускорения и вектор бинормали определяется как векторное произведение двух предыдущих. Разложение ускорения а движущейся точки А на касательную и нормальную составляющие запишется в виде;

a = act + ^bxV,

Рк

где а^ — ускорение точки вдоль кривой С, — скорость точки вдоль кривой С, р^ — радиус кривизны кривой С и V — скорость точки в касательном направлении.

• при движении точки вдоль кривой С касательная вращается вокруг мгновенного положения бинормали с угловой скоростью, равной кривизне к кривой С в точке А;
• бинормаль вращается вокруг мгновенного положения касательной с угловой скоростью, равной кручению т кривой С в точке А, и трехгранник вращается вокруг мгновенной оси, направление которой определяется вектором Дарбу П = т1 + кЬ с угловой скоростью, равной полной кривизне

  кривой С в точке А |П| = л/т^+к^ .

  Все эти утверждения можно отнести к точке на силовой линии поля. Но чтобы все это выглядело не столь абстрактно, можно представить более наглядный образ. Наши реки текут по поверхности земного шара, то есть имеют кривизну, определяемую радиусом планеты. Совокупность вышеприведенных утверждений приводит к немедленному выводу о том, что вода в реке должна вращаться винтом, «ныряя» у одного берега и «выныривая» у другого с частотой кручения. В результате один берег подмывается с шагом винта, а на другой идет намывка плесов, и река приобретает известную всем извилистость русла. Меандрирует.

  Если силовьк линий много и они приобретают характер поверхности, то говорить о кручении уже не приходится. Локально при движении точки по поверхности с кривизной ее должно «сносить» в направлении, перпендикулярном к скорости. Это, в некотором смысле, реликт кручения.

  Читателю, добравшемуся до этого места в моем сочрше- нии, я должен выразить искреннюю благод^ность за проделанный труд и столь же искреннее соболезнование по поводу того, что я не в состоянии передать на этих страницах изумительную красоту геометрических упражнений.

  Оставляя в стороне интерпретацию взаимосвязей касательных и нормалей, геодезических линий и минимальных поверхностей, отметим следующие моменты. Само по себе определение кривизны поверхности (или линии) через радиус соприкасающейся сферы автоматически подразумевает эквивалентность понятия кривизны и некоторой частоты или угловой «скорости», с которой вращается касательная при движении точки вдоль линии или поверхности, поскольку всегда можно определить, если к ~ то и к = где d0 — угол

  поворота касательной при прохождении «точкой» пути dS вдоль линии. Это становится еще более очевидным, если базисные векторы трехгранника Френе выразить через вектор угловой скорости (вектор Дарбу);

  При «nqjexofle» к поверхности с кривизной определение «кручения» теряет смысл, но возникают «преемственные» понятия минимальной и максимальной кривизны поверхности в рассматриваемой «точке». «Взаимоотношения» минимальной и максимальной кривизны регулируются двумя соотношениями, шгорые не зависят от выбора системы координат. Это так называемые средняя и полная (Гауссова) кривизны поверхности:

  1 EN-2FM+GL

  EG-F^

  LN-M^

  EG-F^

  Не утомляя себя и читателя подробным анализом и интерпретациями, отметим, что средняя и Гауссова кривизны выражаются через коэффициенты основных квадратичных форм поверхности (канонические определения поверхности через производные главных векторов) следующим образом:

  В этой записи использованы общепринятые обозначения коэффициентов основных квадратичных форм поверхности. Возможно, в этом месте математики вновь захотят «намьшить шею», но приведенные выражения являются более общей формой для инвариантов, образующихся при лоренцовском преобразовании напряженностей электромагнитного поля:

  Е^-Н^ =inv,

  E*H = inv,

  хотя произведение Е • Н не истинный скаляр, поскольку является лишь частью полного произведения П(Е*Н) = Е*Н + ЕхН.

  Конечно, связь между кривизнами и напряженностями не является непосредственной, поскольку напряженности следует сопоставлять скорее с касательными к поверхности, чем с нормалями. Но в то же время эта связь достаточно однозначна. Сравнение свойств релятивистских преобразований со свойствами поверхности с кривизной в трехмерном пространстве показывает, вообще говоря, необходимость использования представлений не четырехмерного пространства теории относительности, а пятимерного. Действительно, для описания поверхности с кривизной, помимо обычных трех координат, необходимо и задание двух главных кривизн. Но такое усложнение задачи позволяет напрямую установить ряд важных свойств Поля. Инвариант Е^-Н^ естественно сопоставить с сохранением энергии Поля, а Е*Н — импульса. Но для поверхности произведение максимальной и минимальной кривизн является инвариантом изгибания. Отсюда немедленно следует, что существование сферического волнового фронта невозможно, поскольку для сферы обе кривизны одинаковы; К, = Kj= 1/Ксф — ^ одновременное убывание или возрастание их противоречит инварианту Гаусса К,* К2= const.

  Нетрудно сообразить, что его выполнение при эволюции поверхности обеспечивается в достаточно ограниченном числе случаев.

  При К,» К2= о точка принадлежит поверхности цилиндра. Если К|» К2> о, то мы имеем дело с эллиптической поверхностью, и, наконец, Kj« К^< 0 соответствует седловой поверхности, например, однополостного гиперболоида. Однако существует и поверхность, для которой все эти три случая выполняются одновременно.

  Рис. 2.9.2. Кривизна поверхности тора И здесь мы сталкиваемся с уникальной сиггуацией. Если и далее сопоставлять инварианты поверхности с энергией и импульсом поля, то можно, например, потребовать, чтобы для стационарного (в глобальном смысле) поля интегральный поток энергии и импульса был равен нулю:

  Именно такой случай реализуется для поверхности тора. По большому счету в Пустоте ничего и не происходит. Далее, поскольку кривизна имеет еще и смысл частоты (и, может быть, следует напомнить, что энергия и частота в некотором смысле эквивалентны, например, в планковском выражении Е = hv они однозначно определяются друг через друга), то «поверхность» определяется набором характеристических линий, удовлетворяющих «требованиям Лиссажу» для стационарных колебаний. В простейшем случае это кольцевая линия на внутренней поверхности тора, когда Rj = г (см. рисунок).

  Рис. 2.9.3. Простейшая характеристическая линия тора

  Имея в виду частотную интерпретацию кривизны, мы должны предположить и немонотонную эволюцию поверхности. Если в некотором диапазоне ее деформации мы будем наблюдать вращение и движение тора как целого, то радикальное изменение геометрии будет происходить скачком, хотя длительность скачка может быть значительной. Здесь вполне уместна аналогия с развитием плодов. Во-первых, потому, что по форме своей они имеют непосредственное отношение к тору (полярному), а во-вторых, вспомним, завязь очень быстро (несколько дней, неделя) достигает окончательных размеров, а затем длительный многомесячный процесс созревания.

  Возможно, что более развитый анализ геометрических особенностей Поля более удобно и продуктивно осуществлять методом С. В. Руднева, но вернемся к классическим представлениям. Поле в точке однозначно задается значениями векторов магнитной и электрической напряженностей. Интерпретации такого задания Поля имеет смысл уделить особое внимание.

dt as

И

Кср — — (Ктах + Kmin)

Кполн = (Ктах X Kmin) .

1

Кср = — (Ктах + Kmin ) = ^

И Кполн = (Ктах X Kmin) =

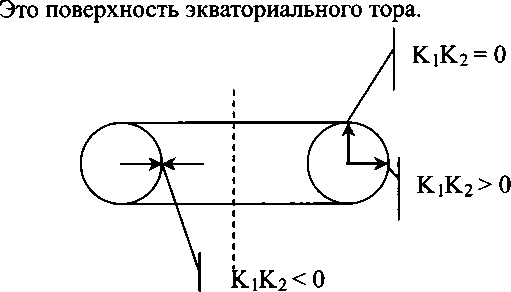
fK,K2=0.

S

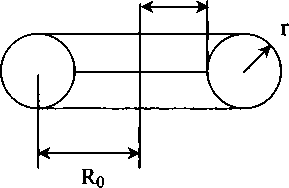
ВРЕМЯ

С точки зрения геометрии Поле есть поверхность (множество их) с кривизной, то есть является пятимерным объектом, в котором евклидово пространство описывается тремя обычными осями и добавляются две криволинейные оси. Причем замкнутые в общем случае, то есть мнимые. Описание Поля — это, по сути своей, описание одной группы осей через другую. Но для этого вводится еще одна координата — время. Очень загадочная философско-физическая категория. В геометрии же это совершенно произвольный параметр, которым иногда удобно воспользоваться.

Многомерность

Понятие «многомерность» — это, пожалуй, одно из самых туманных и загадочных творений человеческого разума. Для человека, привыкшего рассуждать абстрактными, оторванными от реальности, образами, в этом нет ничего особенного. Ну добавил еще одну или несколько осей в известную евклидову геометрию. Что с того, что по прежним правилам ортогональности (перпендикулярности) она (четвертая, например, ось) туда не вписывается. Зато какие элегантные выводы. Какой простор для фантазии. И действительно, многие задачи физического характера решаются в многомерных представлениях куда проще по сравнению с евклидовым трехмерным пространством.

Однако такой подход к постановке вопроса о многомерности — результат, скорее, не развитости ума, а совсем наоборот — его ограниченности. Дело в том, что мало допустить аксиоматически существование или саму возможность присоединения четвертой и далее перпенди1сулярных осей, но следует иметь рецепт, как это сделать. Иначе в полете безудержной фантазии легко скатиться в область психиатрических диагнозов.

Самый здравомыслящий человек — это, конечно, обыватель. И он просто отказывается от подобных рас- суждений, посмеиваясь над «тронутыми» математиками. В этом есть доля вины этих последних, ибо забывают указать тот самый рецепт либо по забывчивости, либо по причине безответственного поверхностного отношения к аксиоматике. Хотя вопрос довольно прост, возможно. Определение перпендикулярности осей в евклидовой геометрии означает, что проекция любой из них на другую обращается в точку, не имеющую измерения. В нулевой объект. И таких объектов может существоватъ великое множество, помимо самих осей. Любая замкнутая совокупность векторов в проекции на евклидову ось дает нулевой результат.

В принципе, эти совокупности принадлежат евклидову пространству и могут быть описаны на евклидовом языке. Но даже для самой простой из них, в виде плоского кольца, придется использовать в описании очень непростые ф)шкции. Что уж говорить о путаных клубках. Но можно просто обозвать ее новой осью. И формализм становится изящным и довольно простым.

Возвращаясь к фигурам Лиссажу, можно сказать, что в их представлении сзчцествует целый набор возможностей. Можно задавать их набором ортогональных колебаний, как мы и поступаем. Можно задать одной или несколькими новыми осями и, наконец, можно вволю повозиться с трансцендентными уравнениями евклидовой геометрии. Но они всегда остаются объектами обычного трехмерного пространства. Даже самые элементарные объекты, как в случае интерпретации С. В. Руднева, описываются пятью осями. Если таких объектов много, то следует говоритъ о множестве новых осей или, что то же самое, о многомерных пространствах. Однако реалъные объекты содержат невероятное количество замкнутъ 1х векторных осей, и здесь возникают определенные трудности в использовании геометрического метода описания. Бумаги не хватит. И здесь существует, вероятно, единственная возможность описания через частотные спектры.

Классическое представление Поля утверждает, что это феномен, развивающийся в пространстве и времени. Правда, преобразования Лоренца и теория относительности заставили сильно усомниться в независимости временной координаты, но ощущение незыблемости ее вполне сохранилось, хотя логикой уже не оправдывается.

Посмотрим на содержание категории Время с точки зрения феноменологии Максвелла. Эволюция напряженности поля во времени здесь увязывается с «распределением» второй напряженности в пространстве, например.

Теперь если корректно подойти к отысканию неизвестных переменных, то из уравнения Максвелла

Проводя аналогию с механикой сплощных сред, мы можем вспомнить, что напряженности электрической можно сопоставить относительную линейную деформацию ^, в то время как магнитной — относительную деформацию сдвига. Отсюда следует еще и то, что эффект времени есть функция деформации пространства. Если пространство не деформировано, то и времени нет.

Таким образом, извратив привычные представления и взяв в качестве исходных аргументов два аспекта Пустоты: электричество и магнетизм, мы должны осознать, что всякий раз, щелкая выключателем, вмешиваемся в таинство течения времени.

i

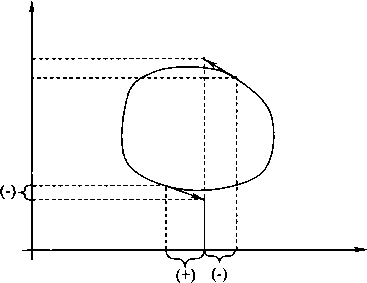
Рис. 2.10.1. Осевые проекции замкнутой совокупности векторов

Хорощо видно, что сумма векторов, являющихся проекциями исходных, дает результат, равный нулю.

Поэтому формально замкнутая совокупность векторов подобна ортогональной оси. Четвертой. И ее действительно можно использовать в качестве таковой. Удобнее, правда, пользоваться очень большой совокупностью коротеньких векторов, замкнутых в виде кольца. Но это необязательно. Любая, даже самая запутанная в виде клубка, совокупность векторов, если она замкнута, все равно обладает теми же свойствами.

А

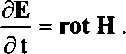
А почему, собственно, не наоборот? Может, следует взять за независимые переменные именно напряженности поля, хотя бы локально? Даже формально система из четырех уравнений (Максвелла) подразумевает отыскание четырех рещений, четырех неизвестных. Как в старой доброй школьной алгебре. И действительно, в отсутствие токов и зарядов система выглядит следующим образом:

— = rot Н

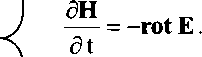
div Е = о

div Н = О

at

Здесь мы положили множитель – = 1. Но эта система и

с

есть поиск четырех неизвестных: трех пространственных и одной временной координаты по заданным Е и Н. Полная система уравнений Максвелла содержит еще три соотношения, позволяющие определить еще три неизвестных, включая заряды и токи:

D = бЕ, В = pH, j = уЕ.

Здесь резонно задать вопрос: если неизвестны только заряды и токи, то почему уравнений целых три? То есть для того, чтобы описывать электрические и магнитные свойства среды, необходимо задание, кроме токов и зарядов, еще какой-то скрытой характеристики. Естественно вспомнить, что у токов и зарядов есть еще и инерционная характеристика — масса, которая в систему в явном виде не входит.

— = rot Н

at

следует определрггь не что иное, как время. Поскольку rot Н соответствует некоторому току j, то, упрощая вид дифференциального оператора rot, получим

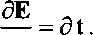
j

Откуда ясно, что Время имеет природу электрического тока. Дикость? А почему бы и нет?

ЭВОЛЮЦИЯ

Каждый раз, щелкая выключателем и бросив мимолетный взгляд на экран работающего телевизора, мы привычно отмечаем рябь помех. Если выключатель зашунтировать небольшим конденсатором, а антенну вынести подальше, то от этого неприятного эффекта можно почти избавиться. Но в чем дело? Телевизор реагирует на очень высокие частоты порядка 10® Гц. В сети частота 50 Гц. Но если бы мы даже пользовались постоянным током, то помехи все равно возникают. Специалист в данном месте снисходительно улыбнется. Но что интересно, так это то, что «знающие» люди немедленно делятся на две, по крайней мере, категории. Одни начнут говорить о том, что скачок тока при включении — это импульс, который на самом деле состоит из бесчисленного количества гармонических составляющих, включая и те, на которые реагирует телевизор. И они правы. Впрочем, правы и другие, которые станут рассказывать о том, что в искре возникает нелинейная среда, в которой генерируются колебания высоких частот. Каждый раз вспоминается в этом случае А. Пуанкаре, утверждавщий, что если есть одно объяснение эффекта, то это немедленно означает, что существует бесконечное множество объяснений его.

Что же происходит на самом деле? Вернемся к свойствам векторов. Поскольку все, что вокруг происходит, — это всего лишь геометрические эффекты, то вполне правомерно и использовать геометрию. Пусть пространство деформируется, и этот процесс описывается некоторым законом изменения во времени. Например, меняется напряженность электрического поля, и это изменение не имеет импульсного характера Е = Ец X cos (cot).

Е ~ COS (cot)

Н ~ cos (cot)

Что означает появление новых компонент векторов? Поле перестает быть поперечным. Для векторов, совпадающих по направлению, возникают и скалярные произведения, а так как большинство гармоник кратны, то это соответствует появлению стационарных структур деформаций в смысле «фигур Лиссажу». И если раньше мы говорили о том, что пространство «забито» Светом до полной его непроявленности — полностью деструктивной интерференции, то теперь должны добавить к этому, что это не просто Свет, а еще и множество проточастиц. Или виртуальных частиц, если угодно. И поскольку возникновение отрицательно и положительно заряженных частиц равновероятно, то в целом пространство по-прежнему электронейтрально. И новое его вещественное состояние скрыто от нас, подобно тому, как глаза наши не видят воздух. Но если изменения атмосферы вполне ощутимы, например, как дуновение ветра или проблемы с дыханием, то «новое» состояние пространства должно каким-то образом быть осязаемым. Здесь мы вновь обратимся к механическим свойствам Поля, но прежде заметим, что протовещество, появившееся в нашем тексте, — это, скорее всего, тот самый пространственный огонь, известный в эзотерике и буддистских (ведических) Учениях о Пустоте. «Пространство заполнено переплетающимися живыми тканями огня и света».

Это означает одновременно, что и напряженность магнитного поля меняется по тому же закону, отличаясь, быть может, фазой колебаний:

Н = Hq X cos (cot + ср).

Для векторов Е и Н существует их произведение, которое, естественно, меняется уже по квадратичному закону:

Р = Е X Н ~ EqHq X cos^ (cot),

но cos^ (cot) ~ cos (2cot), что означает появление удвоенной частоты.

Далее, любая пара из этой тройки тоже имеет произведения:

Е X р ~ cos^ (cot) ~ cos (Scot);

Н X р ~ cos^ (cot) ~ cos (Scot).

Естественно, что следует допустить и все последующие произведения, вплоть до самых высоких частот. Суммарные > P~cos(2cot) векторы, если исходные имели только векторные произведения, включают весь набор гармоник.

и это напоминает ряд Фурье. Хотя с ростом степени (или частоты) тригонометрической функции она всегда меньше исходного значения, но это не означает монотонного снижения напряженности с ростом частоты. Для некоторых компонент она может оказаться достаточно существенной.

МАССА ПОЛЯ

Со времен Умова и Пойнтинга известно, что электромагнитное поле переносит (может переносить) энергию и механический импульс. Это можно прочитать в любом учебнике по электродинамике, поскольку очень многие эффекты определяются именно этими свойствами. Гораздо реже в з^ебниках упоминается (преимущественно в дополнениях или приложениях), что электромагнитное поле переносит еще и момент импульса. Возможно, что с этим свойством Поля связано также большое количество эффектов и явлений, значительных для окружающей реальности, но остающихся пока в тени познания.

Следует заметить, что момент импульса есть всегда, когда есть импульс. Это замечание актуально потому, что очень часто о моменте импульса вспоминают лищь тогда, когда возникает необходимость исследования вращательного движения. Вот тогда и вводится понятие момента импульса относительно точки, являющейся полюсом (центром вращения):

L = г X р,

ведется речь. На самом деле L = г X р — это интеграл (сумма) всех составляющих I, просто при суммировании 1 по всему объему пространства большая часть их направлена навстречу друг другу. Они взаимовычитаются и лишь в «особой» точке складываются, определяя общий ненулевой результат. Однако при прямолинейном движении точки полюсов нет и интеграл равен нулю. Но это вовсе не означает, что в локальных областях пространства момент равен нулю. Здесь мы встречаемся повторно с недоразумением, возникающим при рещении задачи в проекциях. Как в случае с волновыми уравнениями для электромагнитного поля. Сумма проекций компонент вихря на любую плоскость, в которой лежит ось вихря, действительно

Последовательное применение классических представлений к решению задач движения тел в поле других тел, обладающих не толь-

Если электромагнитное поле имеет одинаковые по частоте ортогональные компоненты, удовлетворяющие условиям образования стационарных структур, то вектор импульса является касательной к поверхности (или линии на ней) с характерным размером порядка половины соответствующей длины волны. То есть той, которая «породила» эту стационарную структуру. В этом случае появляется особая точка — полюс, — относительно которой может быть определен интеграл соответствующего момента импульса, т. е. механический момент структуры:

L = —гхР, с

‘ ‘ 4

J • <0 = L.

“”Т’

Классическое определение момента инерции подразумевает наличие некоторой массы, распределенной на «орбите» вращения, то есть

Д _ W _ Iw _h с с я, ’

m = —. сХ,

Естественно, что интегрирование полученного выражения по всем частотам от О до оо приведет к бесконечно большой плотности массы пустого пространства, то есть вернет к проблеме «ультрафиолетовой катастрофы». Вероятно, существует рецепт, по которому следует «сделать» интеграл по частотам нерасходящимся, и тогда определится конечная плотность поля. Но автору такой рецепт не известен. Впрочем, особой нужды в этом, скорее всего, нет, поскольку хотя масса и является существенной характеристикой при макроскопическом описании вещества, но в данном случае вернее говорить о механическом моменте элементарной стационарной структуры поля. При этом если не определены другие условия на взаимодействие этих структур, то интегральный момент локальной области пространства должен быть очень мал или вообще равняется нулю, независимо от количества проточастиц в единице объема. Действительно, механический момент есть вихрь импульса, и взаимодействие двух одинаковых вихрей должно привести к их аннигиляции.

Обычно момент изображают как вектор, перпендикулярный плоскости потока. На самом деле этот вектор соответствует лишь инвариантной части поля момента импульса, которое выглядит точно так же, как и магнитное поле кольцевого тока. Даже если взять систему из двух изолированных вихрей, то «сцепление» полей моментов импульсов заставит их сначала сориентироваться навстречу друг другу, а затем втягиваться в область большей плотности силовых линий.

Не утомляя себя и читателя видом соответствующих математических записей, укажем, что если вообразить на рисунке момент 1, фиксированным, то Ц бу

дет поворачиваться до тех пор, пока пересекающиеся силовые линии не превратятся в противоположно ори- ентированные. Затем начнется втягивание момента в область более плотного поля. Точно так же происходит и взаимодействие двух, например, соленоидов своими магнитными полями. Естественно, что при значительном удалении осей Ij и взаимодействие слабо. Но можно показать, что на конечной стадии сближения интенсивность взаимодействия будет возрастать экспоненциально, пока токовые витки не «слипнутся» друг с другом. Однако гораздо убедительнее формул будут простые опыты с парой кольцевых магнитов, например, от громкоговорителей. Трудно «разлепить» магниты. Затем их взаимодействие быстро ослабевает с удалением друг от друга. «Антигравитацию» можно смоделировать, если сориентировать магниты так, чтобы они отталкивались, и препятствовать их естественному стремлению изменить такую ориентацию на противоположную. Можно заметить, что в любом случае результатом становится достижение минимальной искривленности силовых линий в «области» пересечения. При «антипараллельной» ориентации, соответствующей притяжению, это достигается путем «вычитания» векторов, а при параллельной — вытеснением одного поля из другого.

Разница в принципиальных основах между магнитным и механическим взаимодействиями отсутствует, но соответствующие силы отличаются по величине очень сильно. Это понятно, поскольку в то время, как модули векторов Е и Н равны друг другу, механический импульс определяется их произведением, деленным на квадрат скорости света:

Теперь если вернуться к опыту с двумя зеркалами и проанализировать конфигурации образующихся стационарных структур, то можно обнаружить их чрезвычайное разнообразие, возникающее при различных фазах интерферирующих волн. Причем это не только разнообразие конфигураций, но и «поведение» различных компонент поля: электрической, магнитной и механической.

Многообразие интерференционных структур предполагает, что в одних случаях наиболее существенным будет взаимодействие электрических компонент, и тогда образуется электрически нейтральная пара, например, обладающая магнитными и мехашпескими моментами. Такое образование уже нельзя отнести к проточастицам, хотя и до реальных частиц еще далеко. Пусть это будет субвещество. Взаимодействие магнитных моментов приведет к образованию структуры с электрическим зарядом и механическим моментом, т. е. возникает устойчивый эффект массы. И в определенных ситуациях может решающую роль играть механическое взаимодействие.

Комбинации виртуальных частиц, в которых исчезла одна из компонент поля, хотя и принадлежат ему по-прежнему, но обладают и относительной самостоятельностью. Они не зависят от конкретных волн, их породивших. Кроме того, они имеют все признаки реального вещества: заряд и инерциальность. Дальнейшая эволюция интерференционных структур, обладающих признаками вещества, и порождает все многообразие окружающей реальности.

Мы прошли здесь первый, наиболее важный шаг: от Пустоты к субвеществу. Путь от субвещества к из

вестным элементарным частицам очень правдоподобно представлен, например, Ацюковским в ьсниге «Общая эфиродинамика», и, вероятно, нет нужды повторять его.

Отметим наиболее существенные моменты. Это сочинение, с некоторой претензией на принадлежность к современной науке, показывает, по крайней мере, для автора, насколько мы юны в сравнении с мудрецами древности. Интерференция волн деформации Пустоты приводит к образованию структур, проекции которых напоминают буквы. И вспоминается: «Вначале было Слово…».

Полный импульс Сумма электрических векторов Сумма магнитных векторов

Эволюция интерференционных структур наполняет Пустоту Светом — «Свет имеет природу Пустоты, а Пустота — природу Света». Но далее Свет «пожирается» Субвеществом, в котором трудно не узнать пространственный Огонь древних учений.

Чаша

в большинстве примеров мы оперируем с «чистыми» гармоническими составляющими колебаний. Однако такие компоненты в реальности практически не реализуются, поскольку они просто обязаны быть вечными и бесконечными. Основное голографическое соотношение

Поэтому, рассматривая взаимодействие (интерференцию) двух ортогональных и почти гармонических волн, мы должны учитывать их реальную конечность. Естественно, что гладких и неподвижных структур мы в этом случае не получим. Наличие полосы частот с шириной Асо означает, что всегда существует некоторая расстройка от гармонизма, и, как мы отмечали ранее, расстройка частот означает дрейф структуры. Но поскольку для обеих волн с)чцествует такая расстройка, то, соответствуя ортогональности волн, дрейф тоже образует замкнутую структуру. Можно говорить, что основная структура из гармонических частот (0^ дрейфует по замкнутому контуру Асо. Образуется плоская розетка.

Если углубиться в детали анализа интерференции двух таких почти гармонических волн, то мы должны вспомнить о бесконечном произведении векторов. Зададим соответствующие волны через напряженности электрической и магнитной компонент. И такое задание является исчерпывающим. Далее мы должны определить векторы Пойнтинга. И все просуммировать. У нас получатся суммы импульса — Pj + электрического поля — и магнитного

Голографическая модель вещества, представленная выше, основывается на гипотезе, что все есть деформации пространства, и использует как универсальный инструмент теорию волн и колебаний. В следующих главах этот инструмент будет использован для описания Универсальности Мироздания.

Глава 3.

Для сохранения ясности голографическрк представлений можно было бы, в принципе, ограничиться рассмотрением в рамках классической электромагнитной теории. Тем более что мы опираемся на очень древний и весьма правдоподобный постулат о тождестве Света и Пустоты. Следует напомнить, что под Пустотою здесь подразумевается не пустое пространство, а нечто абсолютное, подобное Богу. Пространство и Время есть всего лишь его аспекты. Причем аспекты не первичные, а производные от внутренне присущих Богу аспектов: Внимания и Восприятия. Так утверждает А. Наумкин в «Калагии»: «И обращаются Внимание в Восприятие и Восприятие во Внимание, порождая непрерывно Пространство и Время». Все можно было бы уразуметь, но какова причина этого обращения, если ею не является сам Бог? Обращение, по сути, означает некоторое Действие или Движение. И здесь приходится смириться с ограниченностью возможности уразумения.

Ограничение же рамками классического электромагнетизма тянет, неоправданно, за собой шлейф неопределенности многих физических понятий. В предьщу- щей главе, вслед за Уиллером, мы показали возможность существования заряда без заряда и массы без массы.

Впрочем, это вполне естественно: измерять высоту высотами, длины — длинами, массу — массами, а силу — силами. Иногда удается установить между ними соответствие в виде размерных или безразмерных коэффициентов. Например, задав эталонную высоту, можно установить ее связь с эталонной длиной в виде безразмерного коэффициента. Тогда становится ясно, что это величины одной природы — геометричеоюй в данном случае. Хуже, 1Ю1да коэффициенты соответствия имеют размерность. Из порочного круга выйти очень трудно.

Столь же неопределенно, как и сила, понятие «энергия», этимологически означающее возможность совер- щить определенную работу. А что такое работа? И т. д.

где г — радиус-вектор «точки», обладающей импульсом р. Причем вектор L практически всегда совпадает по направлению с угловой скоростью. И на самом деле, если мы имеем стационарную вращающуюся систему, то такого определения вполне достаточно. Но классическое определение момента импульса не связано с выделенной точкой или осью. По существу это определение некоего кинетического поля, поскольку соответствующий вектор можно определить для любой точки. Более того, можно определить линии, вдоль которых этот вектор имеет одинаковую длину, то есть «силовые» линии.

Рис. 2.12.1. Силовые линии поля момента импульса

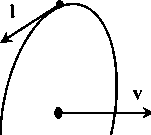
Естественно, если точка с импульсом р движется по кривой с радиусом R, то в центре кривизны какие-то \ У’ 1 компоненты I сохраняются,

| ‘^ и именно о них чаще всего

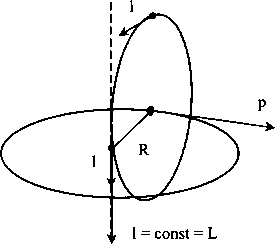
равна нулю. Если только ось вихря прямолинейна.

Рис. 2.12.2. К определению момента импульса

КО гравитационной, но и кинетической составляющей, т. е. имеющих поле момента импульса, приводит к весьма интересным результатам. Например, траектории спутников не могут быть плоскими, и отклонение тел в поле тяготения зависит от направления подлета: по вращению или против вращения тяготеющего тела. Но нас сейчас интересует другое.

ж 1

X,

где Irl = _, а Р — вектор Пойнтинга.

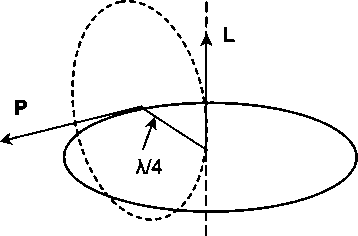
Рис. 2.12.3. К механическому моменту стационарного поля

Механический момент может быть выражен через стационарную характеристику — момент инерции J и частоту обращения вектора Пойнтинга вокруг полюса:

Если скорость распространения волны по-прежнему с, то

4с

и так как

1 Т 1?

Jw = —-Р, откуда J = -|Р|.

с^ 4 16с^

J = mr =m—,

16

и можно говорить о массе стационарной структуры поля

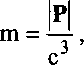
Р

где импульс ^ может быть определен из энергии План-

ка для поля с частотой v

что приводит к известной формуле Комптона

h

ВЗАИМОДЕЙСТВИЯ

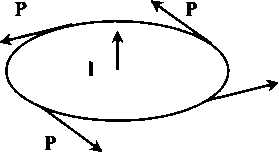
Рис. 2.13.1. Механический момент

В результате — аннигиляция при одинаковых Р и 1 либо соосная ориентация

их с суммарным 1 = 1,-12- Точно таким же образом происходит механическое взаимодействие и реальных частиц, включая микро-, мезо- и макрообъекты. По сути, речь идет о гравитационном взаимодействии, механизм которого, конечно, не сводится к чисто потенциальному притяжению двух тел.

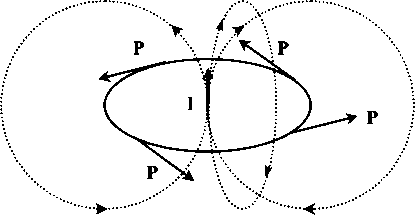
Рис. 2.13.2. Поле момента импульса

Следует всегда учитывать, что масса — это функция от интеграла механических моментов, и гравитационное взаимодействие подобно магнитному, где отталкивание возможно лишь в том случае, если существует некоторый механизм, препятствующий адекватной ориентации моментов.

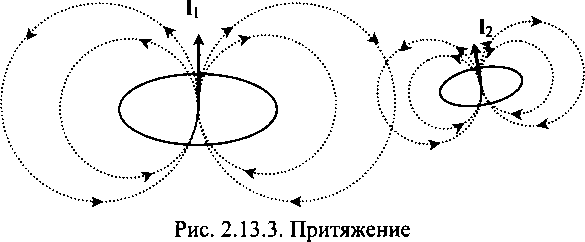
Рис. 2.13.4. Примеры интерференции двух плоских волн

Еще более затейливые фигуры образуются при интерференции волн с кратными частотами, среди которых мне особенно притягательна структура, образующаяся при интерференции трех взаимно перпендикулярных волн с соотношением частот 2:3:3. Это связано с тем, что в спектре внутренних произведений это наиболее интенсивные ортогональные колебания, которые наглядно демонстрируют своей трехпетлевой структурой, что рассуждения о кварках были небеспочвенны.

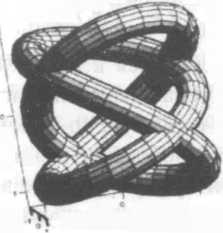
Рис. 2.13.5. Пример трехмерной интерференции

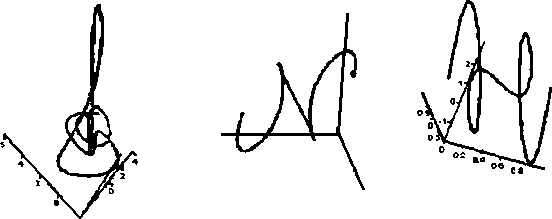
Рис. 2.13.6. Проекции стационарных структур и современные буквы

X

АсоДт ~ 1

дает для бесконечно узкой полосы частот Дсо^О и Дт^оо, что и означает вечность существующего колебания. Если даже допустить, что такие процессы происходят, а в реальности мы наблюдаем их некоторые комбинации cOq± Асо, то проблема проще не становится. Как говорят: что в лоб, что по лбу.

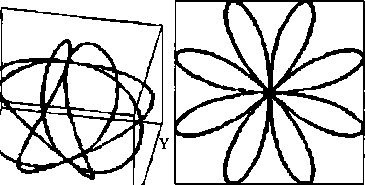
X —— 1/

Проекция на Z,0,Y

Рис. 2.13.7. Розетка

И

Проекция на Z,0,X

поля — Н, + Hj. Но произведение Р’ = (Ej + Е^) х (Hj + Н^) вовсе не совпадает с вектором Р, + Р^, и мы должны теперь определить новую сумму импульса. Ясно, что мы возвращаемся к бесконечному произведению, с возрастающими частотами. Но поскольку мы имеем дело с реальными длительностями или протяженностями исходных колебаний, то результат сложения вновь представляется в виде розетки. Новая розетка получается не плоской, а в виде чаши. Более того, в самой чаше находится некая более высокочастотная структура, видом своим напоминающая из древних сочинений: Будда медитирует в чаще своей… Что он там медитирует — это отдельный разговор. Может, новую Вселенную.

НАПРЯЖЕННОСТЬ ИМПУЛЬС ЭЛЕКТРИЧЕСКАЯ

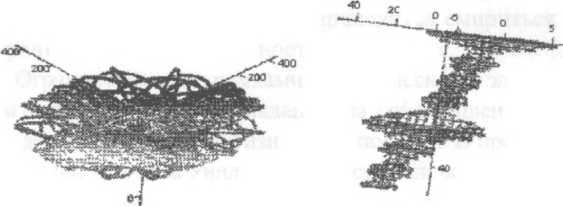
Рис. 2.13.8. Чаша

А

ЭНЕРГИЯ И ВЗАИМОДЕЙСТВИЕ

объяснив появление новых характеристик изменением структуры пространства. Можно было бы, следуя термодинамическим традициям, сказать, что новые характеристики возникают вследствие изменения энтропии пространства. Это ровным счетом ничего не дает в понимании того, что же есть на самом деле заряд и масса. Кроме того, что они возникают «по вине» электромагнитного поля. Поле характеризуется либо напряженностью, либо потенциалом, а следовательно, заряд и масса соответствуют некоторым распределениям этих характеристик в пространстве. Но понятия «напряженность» и «потенциал» определяются через силу, действующую на «единичный» пробный заряд, либо через энергию последнего. Круг замкнулся, ибо заряд определяется структурой поля, а поле определяется через силу, действующую на заряд. Кроме того, сэр Исаак Ньютон, введя понятие «сила», не позаботился определить ее поконкретнее. И фигурирует оно как мера взаимодействия, замьпсая собою порочные круги определений без определений.

ДЕФОРМАЦИИ

В предыдущей главе уже упоминалась идея Эйлера, позволившая ему подобрать ключи к описанию упругих свойств тел. Он перестал обращать внимание на конкретную причину свойств, считая тело «куском пространства» с определенными свойствами. И оказалось, что поведение упругих свойств можно описывать всего лишь двумя типами деформаций: продольных (сжатие и растяжение) и поперечных (сдвиг). Глубокая аналогия между упругими свойствами и «поведением» электромагнитного поля подкрепляется и формальным родством соответствующих математических образов. Уравнения Максвелла повторяют уравнения деформаций.

Трехмерные деформации описываются наборами (тензорами) чисел, анализировать физический смысл которых — задача не из простых. Там существуют проблемы наглядности. Однако существуют и весьма доступные изучению примеры статических деформаций. При небольшой величине последних хорошо работает закон Гука:

Здесь А1 — удлинение (сжатие) образца в направлении действия силы F;

1 — длина образца;

S — сечение образца в плоскости, перпендикулярной силе F;

Е — модуль Юнга, тот самый коэффициент, устанавливающий соответствие между геометрическими эталонами и «силовой» шкалой, в данном случае он не только имеет размерность, но и характеризует упругие свойства материала образца.

Например, модуль Юнга для стали в десять тысяч раз больше, чем для резины.

Смысл закона Гука удивительно прост: относительная деформация А1/1 пропорциональна напряжению F/S. Последнее соотношение в механике сплошных сред имеет и другое название — давление, которое чаще используется в отношении газов и жидкостей, где вьщелить направление силы можно лишь как перпендикулярное к поверхности, ограго1чивающей среду. Все остальные направления действия силы «компенсируются» в соответствии с законом Паскаля. Если ограничивающей поверхности нет (атмосфера, например), то понятие давления — как поверхностная плотность силы, вообще говоря, теряет смысл. Что это за сила, которая направлена равномерно со всех сторон (или во все стороны)? Действие ее (точнее, в соответствии с механикой, равнодействующая) равно нулю, и говорить не о чем. Сила, по определению, — величина векторная, т. е. имеющая направление. Здесь же суммарный вектор равен нулю. Ни значения (величины), ни направления. То есть понятие давление имеет смысл лишь при некотором взаимодействии на границе среды (поверхности), как потенция (возможность) совершить нечто. Какое-то действие, работу. Последние два термина в физике неэквивалентны. Работа определяется как скаляр (инвариант), характеризующий перемещение чего-либо под действием силы:

Обычно записывают не так: А — работа; А1 — перемещение; F — сила и

Действие (как определение) возникает в развитии механики и означает произведение работы на время, в течение которого она осуществлена:

Поэтому физическая терминология требует к себе деликатного отношения.

Через возможность (потенцию) совершить работу определяется чрезвычайно важное понятие — энергия. Важность заключена в гипертрофии применений. Вплоть до мировоззренческого статуса, который хотя и менял свои названия от энергизма до разноцветных по- зитивизмов, но, по сути своей, всегда имел, мягко говоря, несколько неопределенную природу. Вплоть до курьезов. Например, ценность пищи (корма) тоже решили определять через энергетические характеристики. И определяют до сих пор! Как? Очень просто. Сжигают и определяют количество выделенной энергии (теплоты). Удивительно, что до сих пор не перешли на питание керосином. Он-то больше всего выделяет теплоты (калорий) при сжигании.

В молекулярно-кинетической теории и термодинамике, где доминирующую роль играют химические взаимодействия, энергетические представления, основанные на вероятностном описании, «работают» с поразительной точностью. Это обстоятельство и закрепило достаточно косное определение «закона сохранения энергии». Энергия может менять свой «статус»: от потенциальной до кинетической, например, — но вроде бы ее общее количество не меняется. Из этого «закона» возникло множество недоразумений. Выше уже упоминалась одна из подобных проблем: ультрафиолетовая катастрофа. Действительно, по закону сохранения энергии в высокочастотной области спектра излучения должно получаться бессмысленно большое количество этой самой энергии. С точки зрения термодинамики должно быть очень горячо. На самом деле ничего подобного не наблюдается. И добрая «дедовская» механика абсолютно прозрачно объясняет несостоятельность этой проблемы. Работа определена изначально как произведение равнодействующей силы (т. е. векторной суммы всех действующих сил) на вызванное ею перемещение. Если же суммировать (по закону аддитивности или сохранения) все виртуальные (возможные в данном случае) «работы», то результат может (и должен) оказаться бессмысленным.

В теории (классической механической) энергия определяется как скалярная часть произведенрм силы на вызванное ею перемещение. Именно скалярная. Другая, векторная, составляющая этого произведения никакого отношения к работе и энергии не имеет и называется моментом силы. Эта часть «произведения» не совершает работы, но «важна» ввиду того, что меняет направление движения. Классическая механическая теория автоматически подразумевает, что если на «материальную точку» одновременно действуют две одинаковые по закону изменения, но противофазные силы, например:

Термодинамический (вероятностный) подход этим обстоятельством как-то пренебрег и дает сумму независимых действий. Но, напомним, в химии и, собственно.

t

Закон сохранения энергии «напрямую» не работает и в физике ядерных процессов. Здесь приходится говорить уже о комбинации законов сохранения энергии и массы в известной форме

При распаде ядра сумма масс «осколков» оказывается всегда больще массы «развалившегося» ядра, а при «слиянии» ядер (синтез) образовавшееся ядро всегда «легче» суммы масс объединившихся. Короче, полная неразбериха.

Но очень часто «закон сохранения» (все законы сохранения) — очень удобная штука. Очень практичная. Но не в гносеологическом смысле. Потому как за рамками познания в этом случае остаются вопросы типа: что такое энергия, масса, заряд, сила?

Многословный пассаж по поводу закона сохранения энергии для кого-то из читателей покажется бессмысленным по содержанию, а для кого-то и вовсе не даст ничего для понимания проблемы, но он совершенно необходим для автора. Вернемся вновь к закону Гука.

Давление F/S все-таки имеет смысл, но, конечно, не векторный. И это легко понять, если «домножить» числитель и знаменатель на некоторую длину. Пусть это будет длина образца, к которому приложена сила F. Тогда (F1)/ (S1) по-прежнему остается давлением, но в числителе уже величина, по смыслу имеющая значение потенциала ф = F1 (т. е. возможность совершить работу), а в знаменателе — объем образца. Отсюда становрггся прозрачным смысл «ненаправленного» давления. Это объемная плотность потенциала. Напомним, что возможность (потенциал) совершить работу и работа — это не одно и то же. Чтобы потенциал «превратился» в работу, нужны некоторые условия. Например, камень, лежащий на горе, обладает потенциалом. Если его столкнуть с горы и он упадет к ее основанию, то совершится некоторая работа. Но в нее превратится не весь потенциал, а только его часть. Поэтому в большинстве случаев абсолютным значением потенциала интересоваться не имеет особого практического смысла. Важна только его разность, выразившаяся в произведенной работе. Или которая может так выразиться.

И Работа, и Потенциал пропорциональны Силе, но это не является признаком их «панибратства». Если обозначить в данном случае давление (объемную плотность потенциала) через традиционно используемое в

То есть основные физические понятия являются, по существу, геометрическими. Из выражения

По первому пункту отошлем критически настроенного читателя к идеям самого Эйлера. Ему, наверное, было нелегко вообразить кусок металла или камня просто областью пространства, но он смог. По второму пункту возражений можно пойти на некоторый компромисс. Да пусть, в конце концов, не сама Пустота деформируется, а та самая ткань Огня и Света эзотерическая, что обсуждалась в предыдущей главе. Хотя, в принципе, это одно и то же. Но можно как-то смириться.

Выше мы исследовали, вслед за классиками, «геометрию» твердых тел. А что «дают» газы? Вспомним уравнение состояния для идеального газа, носящее имя великих Менделеева и Клайперона:

Удельную газовую постоянную В = R/p (универсальная газовая постоянная, деленная на молекулярную массу данного газа) можно сопоставить с характеристикой, близкой по смыслу модулю Юнга. Тогда объемная плотность потенциала р, умноженная на объем, в котором он «заключен», — рн, естъ попросту потенциал единичного объема и «выражается» температурой Т. Здесь следует иметь в виду, что н — это удельный объем газа, то естъ, по сути дела, величина, обратная плотности газа:

Здесь возникает (вернее, автор протащил) не только понятие температуры, но и понятие массы газа, да еще и молекулярного веса газа. Но и возникает забавная коллизия — выражение:

Если более определенно отнестись к примеру газов, то мы должны вспомнить закон Майера о связи теплоемкостей в процессах с постоянным объемом — и постоянным давлением — С :

Отношение Ср/С^ = у называется показателем адиабаты, а скорость звуковых волн в идеальном газе определяется как

Конечно, автору хотелось подчеркнуть, прежде всего, геометрическую суть левой части уравнения состояния: pV = RT, но неизбежно возникло представление массы (или плотности ее). Оставляя это на «потом», туда же отнесем и чрезвычайно важные понятия закона Майера и CJC^, которые имеют самое непосред

В отношении газов более применимо понятие объемной упругости. Впрочем, это понятие применимо к любым средам, если силы (растягивающие или сжимающие) равномерно распределены по направлениям в пространстве. Это, собственно, и составляет содержание закона Паскаля и определение (устоявшееся) давления. При этом, конечно же, справедлив закон Бой- ля-Мариотта для идеальных газов:

V2 = V,+AV и

Р2 = Р,-ДР-

Если записать закон Гука для деформации диэлектрика под действием электростатических сил, например, стеклянная пластина с проводящим покрытием (конденсатор), то сила в соответствии с законом Кулона

Ad^

d E4яeoed^S’ или, так как Ad • S = AV,

Но если бы только одними «вакуумными» свойствами, то в знаменателе следовало ожидать число, равное единице. Отсюда следует, что несусветно большие величины модуля Юнга, а для большинства твердых тел они имеют порядок 10’“-^ 10″ Па, характеризуют свойства самой Пустоты. Равно как и электрическая постоянная е^. В определении электрических свойств конкретного вещества существенна относительная диэлектрическая проницаемость, которая, как правило, имеет величину порядка первых единиц. Лишь иногда эта величина имеет значения в сотни и тысячи раз большие. Это характерно для пьезо- и сегнетоэлектри- ческих кристаллов.

Вероятно, и определение модуля Юнга было бы корректнее записывать через произведение некоторой механической постоянной и относительной Ej, подобно тому, как это делается в отношении диэлектрической проницаемости. Впрочем, механическая постоянная, видимо, хорошо известна под названием «гравитационной постоянной», имеющей величину около у = 6,67 • 10 ” Н м^ кг^. Если этот коэффициент пропорциональности записывать не как принято, в числителе закона всемирного тяготения, а в знаменателе, куда в законе Кулона помещают электрическую постоянную, то величина 1/у ~ 1,499 • 10’® по порядку числа очень близка к значениям модуля упругости многих твердых тел.

Здесь сразу же возникают проблемы несоответствия размерностей и туманности смысла взаимосвязи механических и электрических свойств пространства. К сожалению, у автора нет рецептов ни к установлению связи, ни к формализации ее. Но попробуем разобраться на качественном уровне хотя бы.

Хотелось бы сразу оговориться, что модуль Юнга, как упругая характеристика, применим только к твердому

в предыдущей главе, в опыте с зеркалами, мы рассмотрели возможность образования продольных волн, т. е. таких, для которых смещения параллельны направлению распространения. На самом деле при интерференции ортогональных волн возникают не только стационарные объекты, для которых div Е О, что соответствует появлению электрического заряда, но и в «з^егающей» волне появится компонента с продольной составляющей. По классике это очень стремительная волна. Можно было бы интерпретировать сказанное и по-иному. Если инвариантом скорости распространения является произведение групповой и фазовой скоростей, то при интерференции гр5Ч1повая скорость обратилась в iiyab, — возник стационарный (стоящий на м есте) объект. А следовательно, фазовая скорость обратилась в бесконечность.

Рассматривая электромагнитное поле, мы пользуемся понятием «напряженность», что есть сила, действующая на некоторый неподвижный пробный заряд. Хотя наличие заряда нужно, вообще говоря, только при измерении. Сила, по выше рассмотренному, есть изменение объема в определенном направлении и выражается в единицах площади. Нас не должно смущать определение «изменение объема», если мы держим в уме несжимаемостъ. Это легко понять на наглядном примере. Вода практически не сжимаема, но, будучи налита в эластичный пузырь, может принимать форму по обстоятельствам. И хотя ее общий объем не меняется, но деформации его могут быть значительными.

С другой стороны, инвариантом в преобразовании Лоренца является не трехмерный, а четырехмерный объем. Точнее, произведение трехмерного объема на собственное время: Vt = v^x = inv. Пусть V = v + Дv и Av мало, тогда (v + Av) t = VT. И пусть t = т – Ат, где Ат О, тогда VT + AvT – Atv – AtAv = VT,

Это означает, что относительное изменение трехмерного объема соответствует относителъному изменению времени. Но (Av/v)^ ~ w — плотностъ энергии и, следо- вателъно, (Ат/т) ~ w’^^. То есть при сжатии (и растяжении) трехмерного пространства изменяется не только плотность энергии, но и время, а инвариантом является то, что определяется как действие.

Итак, напряженность поля при интерференции волн образует структуру растяжения либо сжатрм пространства. Естественно было бы ожидать, что эта структура очень быстро релаксирует к некоторой средней «плотности» пространства, и ни о каких стационарных объектах говорить бы не пришлось. В предыдущей главе мы обсуждали проблему понятия «масса» и пришли к выводу, что эта характеристика имеет чисто динамическую природу. Впрочем, как и электрический заряд. Помимо этих характеристик интерференционный узел обладает еще и магнитным моментом, т. е. структурой, образованной магнитной составляющей исходной волны (или исходных волн).

Это вполне естественно было бы ожидать, поскольку мы привыкли задавать поле совокупностью электрической и магнитной компонент. На самом деле здесь существует определенная тонкость. Если с электрическим полем, надеюсь уже ясно, следует связать деформацию сжатия (растяжения) пространства (что, кстати, объясняет наличие отрицательных и положительных зарядов), то магнитное поле, хотя и подобно в чем-то электрическому, имеет несколько иную природу. Магнитное поле мы привыкли связывать с движением электрических зарядов — электрическим током. То есть для существования второй компоненты электромагнитного поля необходимо некоторое движение. Процесс, связанный с понятием время. Уже говорилось об инвариантности (относительно преобразований Лоренца) произведения трехмерного объема на время: Vt = inv. Отсюда следует сделать осторожный вывод о том, что с изменением объема связано происхождение времени.

Максвелловская теория электромагнетизма напрямую указывает на эту связь. Напомним уравнение

Таким образом, классическое определение электрического тока через движение зарядов можно рассматривать как частный случай, но, скорее всего, оно просто некорректно и переворачивает проблему с ног на голову. Наличие подвижных зарядов, т. е. проводящих сред, позволяет решить проблему направленного, канализированного тока. Но не более. Сам ток в зарядах не нуждается. Это хорошо иллюстрируется, например, на конденсаторах, где «диэлектриком» является вакуум, и ни о каких зарядах говорить не приходится. Конечно, постоянный ток в проводящих средах является важнейшим частным случаем, но использование его в качестве определения тока вводит в заблуждения. Электрический ток является эффектом времени, которое можно рассматривать в качестве некоторой субстанции. И именно время удерживает «пузырь» «надутого» или «разреженного» пространства от релаксации. Термин «пузырь», как образ элементарной частицы, использовал в шестидесятых годах двадцатого века томский профессор Борис Николаевич Родимов.

Далее мы будем использовать привычные понятия электрического и магнитного полей, но и будем стремиться удержать в памяти при этом, что электрическое поле — это деформация трехмерного пространства, а магнитное — эффект времени.

Не вдаваясь в тонкости математического анализа, но имея в виду гиперболическую связь трехмерного объема и времени

Но все это формализм, который достаточно труднопредставим в наглядных образах, хотя мы теперь и имеем представление о направлении времени и «происхождении» понятий «сила» и «энергия». И проблема наглядности образов скрывается, похоже, не в недостаточной проработанности известного математического формализма, а в самой его аксиоматике. Действительно, чтобы выйти из круга идей механистического детерминизма, в свое время пришлось отказаться от аксиоматики трехмерного евклидового пространства и обратиться к четырехмерному, в котором пространство и время уже не являются неза-

Здесь, конечно, не все понятно и с трехмерной аксиоматикой. Скажем, длину и ширину мы можем измерить без особого труда, передвигаясь по поверхности постоянного потенциала, например, по земле. Но измерение высоты требует использования лестницы и определенных энергозатрат, хотя бы для того, чтобы по ней подняться. За этой шуткой скрыт определенный смысл, даже в том случае, когда мы пользуемся теодолитом и тригонометрией. Возникает поворот. А это вновь возвращает к проблеме времени.

I ~ ES’

Д1 = Е/А.

A = F аТ.

D = At.

F, = F^sin (cot);

Fj = FgSin (cot + я),

то результат их действия (а следовательно, и изменение энергии), вообще говоря, не наблюдаемы.

в термодинамике это несущественно. Однако в оптике такое «прямое» применение закона сохранения энергии просто недопустимо. Там, где колебания (волны) имеют одинаковые фазы, энергия (интенсивность) больше простой суммы отдельно подсчитанных для каждой составляющей, а для области (или ситуации) с противо-

положными фазами интенсивность может вообще «не состояться». То есть волны (излучение) вроде бы есть, но не наблюдаются. (Деструктивная интерференция).

Е = тс^.

В случае закона Гука реализацией потенциала будет абсолютное удлинение образца А1. Произведение

—F • А1 — это, конечно, произведенная работа. Коэффи-

деформации сила F = 0, а в конце принимает значение F. Если правую часть выражения — = — умножить и

разделить на А1, — =

А1_ 1 FA1

’ 1 “es-аГ

1 ES

то относительное удлинение, оказывается, характеризует не что иное, как объемную плотность работы AA/AV, так как S • А1 = AV есть изменение объема. Можно преобразовать закон Гука и к виду

А18 = – Р1или АУ = – ю,

Е Е \

что означает пропорциональное изменение объема (геометрическая характеристика) абсолнлной величины потенциала. Потенциал — сугубо физическая категория, имеющая некоторое отношение и к энергии, и к давлению, — оказывается, ршеет простой геометрический смысл. Потенциал характеризует изменение объема. И ничего более. Конечно, «пространство» может оказаться очень разным. Но это различие «заключается» в модуле Юнга, который в любом случае всегда остается просто коэффициентом пропорциональности, характеризующим свойства именно этого «куска» пространства. Сила F так же приобретает простую геометрическую интерпретацию:

F = E-

AV

1

как величина изменения объема в направлении длины 1. По сути математической (геометрической) — это просто градиент деформации объема.

механике понятие напряжения о = у^, то изменение работы, равное, естественно, запасенной потенциальной энергии:

А = Е„„=|РД1,

-F/’

F = oS и

И так как из закона Гука

W а

V 2Е

ТО объемная плотность энергии

пропорциональна квадрату объемной плотности потенциала. Отсюда геометрический смысл плотности энергии

Е ( AV V

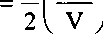
W

Соберем полученные выводы вместе:

Сила F = Е grad AV = ^

Энергия = работа =

E(AV)2

Энергия = работа = ————;

Потенциал ^ = Е А V.

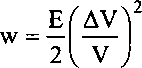
при AV = V следует, что модуль Юнга Е = 2 w численно равен удвоенной объемной плотности энергии при увеличении объема в два раза. Можно, безусловно, выбрать такую систему единиц, что модуль Юнга будет безразмерным и равным единице (Е = 1). Тогда плотность энергии (объемная) будет просто безразмерной величиной, энергия (работа) и потенциал будут измеряться в единицах «объема», а сила — в единицах «площади». «Голая» геометрия. Здесь полезно вспомнить, что модуль упругости — величина по смыслу обратная сжимаемости. Если вообразить некую среду, не способную сжиматься, то модуль Юнга обращается в бесконечность, а вместе с ним и энергия, и потенциал, что довольно бессмысленно. Для многих из тех, кто усердно добрался до этого места текста, приведенные рассуждения представляются в крайнем случае рафинированной шуткой для рафинированного специалиста. Во-первых, потому что как-то «безосновательно» обобщаются достаточно специальные положения механики сплошных сред, которые в современных курсах физики если и упоминаются, то на третьем плане, не ближе. А во-вторых, ну нельзя же всерьез обсуждать деформации самого пространства.

рц = ВТ.

Здесь р — давление (сила, деленная на площадь), совершенно непонятное определение, если не иметь в виду поршней или других поверхностей, на которые «давит» газ; V — естественно, объем газа; В — удельная газовая постоянная; Т — температура газа.

V

М

р = —, то есть ц = —,

V М

где М — масса газа.

PV = Mrt

ц

можно представить в виде

р RT

Р Ц ’

М

где, естественно, р = —.

Если чуть отрещиться от «газовой» сути предпо-

RT

следнего выражения в его правой части —, то смысл

, Р

отношения р/р есть квадрат скорости распространения возмущений в среде. Более точно это можно адресовать только к скорости поперечных волн в струне, но, введя понятие массы, мы невольно подходим к сугубо динамическим понятиям. По крайней мере, к кинематическому понятию — скорость.

Ср-с„=-р.

Y

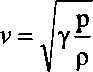
или

v = VyOT.

ственное отношение к чисто геометрическим понятиям средней и полной (Гауссовой) кривизны.

pV = const,

в частности

P,V, = P,V,.

Если изменение объема (или давления) мало, то можно записать, например,

Далее, пренебрегая малым по величине произведением aVAp, получим

V

AV

Последнее выражение в механике твердых тел соответствует закону Гука для деформации всестороннего растяжения (ежатия)

а = К

Здесь AVA^ — по-прежнему относительное изменение объема; а — напряжение и К — модуль объемной упру- гоети. К связан с модулем Юнга через коэффициент Пуассона:

К = .

3(1-2ц)

Коэффициент Пуассона устанавливает связь между продольным отноеительным удлинением и сопровождающим его относительным сужением:

Ad А1

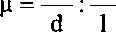
Сопоставляя смысл выражений законов Бойля-Мариот- та и Гука для объемной деформации, можно довольно наглядно пояснить смысл модуля Юнга: Ар соответствует такому изменению давления величиной р, которое вызывает относительное изменение объема АУ/У.

Но смыел давления р состоит в том, что оно задано внешним образом (сосуд с поршнем), поскольку газ счи- хается состоящим из отдельных, практически не взаимодействующих между собой частиц. Классическая теория считает, что они «общаются» между собой, лишь соударяясь. Но если «энергетический» смысл р эквивалентен таковому для модуля объемной упругости, то твердое тело обладает собственным «давлением», которое определяется взаимодействием между частицами.

Здесь Q — заряд каждой проводящей поверхности; 8q — электрическая постоянная (диэлектрическая проницаемость вакуума — Пустоты); е — относительная диэлектрическая проницаемость стекла; d — толщина стеклянной пластины. Подставляя приведенную силу в выражение

d ~ES’

где Е — модуль Юнга, а S — площадь пластины, получим:

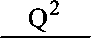
Е47С8ое

Для стекла Е ~ 8 • 10’® Па; е ~ 8 и для вакуума ~ 8,85 • 10 ‘^ Ф/м. В знаменателе получаем 8 • 10‘® • 4 • 3,14 • 8,85 • 10 ‘^ • 8 ~ 70. Это позволяет предполагать, что взаимодействие (внутреннее давление) в стекле обусловлено в значительной мере именно электрическим полем. А, по сути, свойствами самого вакуума — Пустоты.

телу. Более общей характеристикой является коэффи-

£

циент объемной упругости К = или обратная

3(1 – 2 р)

ему величина—сжимаемость. Эта характеристика применима и к твердым телам, и к жидкостям, и, в какой-то мере, к газам. Очевидно, что при ц = 1/2 упругость обращается в бесконечность. Точнее говоря, становится неопределенной. Но одновременно это означает, что сжимаемость становится равной нулю, то есть объем (обычное трехмерное пространство) является инвариантом. Это не означает, что его нельзя деформировать, но деформации допустимы лишь определенного рода — сдвиговые. По определению сдвиг есть деформация, не меняющая размеров образца, но меняющая углы между его сторонами.

/		7^ >
<			Г

Рис. 3.1.1. Сдвиг

При этом, естественно, сохраняется и объем образца. Отсутствие объемной сжимаемости Пространства имеет следствием вывод о том, что в нем могут распространяться только поперечные электромагнитные волны, имеющие сдвиговую природу. Следует, правда, оговориться, что, в соответствии с классической теорией, отсутствие сжимаемости (ц = 1/2) не означает невозможности продольных волн, а лишь указывает на то, что скорость их распространения очень велика. Бесконечно велика, а взаимодействия мгновенны?

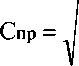
Ё~ 1-р Р (1 + ц)(1-2р)

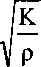
или при ц = 1/2

Спр =

и если К 00, то и С оо.

С2 = С C=inv

гр ф

и если — известная константа, то при = О, Сф = оо.

и если пренебречь в первом приближении малой величиной AtAv, то получаем

AvT = Atv

или

Av _ Ат V т

di

= rot Н,

с учетом того, что rot Н = J, то есть магнитное поле не есть проявление электрического тока, а им самим и является в случае, когда можно выделить совокупность векторов Н, касающихся некоторой замкнутой линии, приводит к выводу о теснейшей связи магнитного поля и времени. Вспомним, что напряженность имеет смысл силы, а та, в свою очередь, характеризуется изменением объема вдоль выбранного направления. Тогда уравнение Максвелла в форме

-^ = 1

ЭЕ ~ J

показывает, что 1/J есть плотность времени. Далее, если считать ток функцией электрической напряженности J = f (Е), то формальное интегрирование уравнения Максвелла приводит к логарифмической зависимости времени от электрического поля, то есть, по существу, от деформации пространства

дЕ

f(E)

dt =

и

t~klnf(E) + C.

В последнем выражении могут оказаться существенными множитель к и постоянная интегрирования С, но сейчас интересно то, что время может обращаться в нуль, а также принимать положительные и отрицательные значения. То есть по разные стороны некоторой поверхности (рис. 3.1.2), охватывающей деформированную область пространства, время течет в разные стороны!

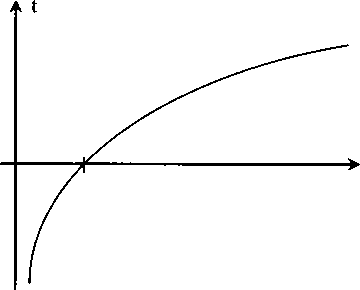
Рис. 3.1.2. Сечение поверхности деформированной области пространства

_ const t

автоматически получаем для градиента деформации (сила), а соответственно, и для плотности энергии по обе стороны ограничивающей поверхности (на которой интеграл для времени обращается в нуль) следуюп^ую качественную картину вдоль одной из осей.

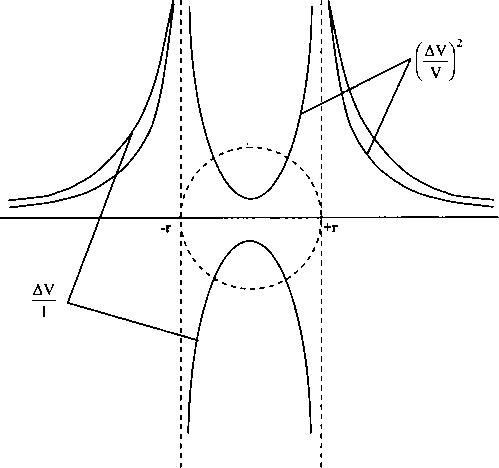
Рис. 3.1.3. Силы и энергия «пузыря» растяжения

Это соответствует «пузырю» растяженрм. При замене течения времени на обратное, то есть при f = -t, полу-

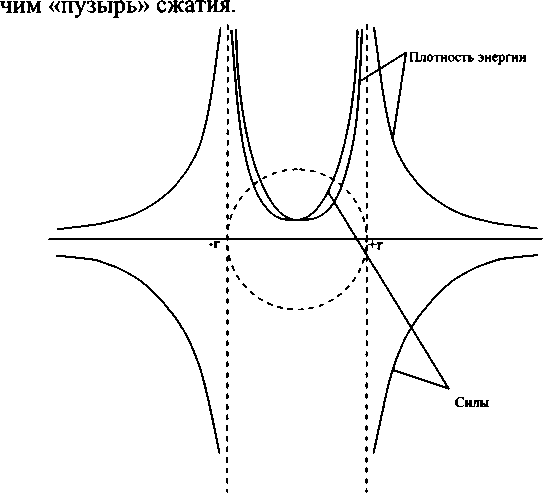
Рис. 3.1.4. Силы и энергия «пузыря» сжатия

висимыми. Из этого возникла теория относительности. Затем потребовалось еще почти столетие, чтобы осознать многомерность времени.

ГЕОМЕТРИЯ ВРЕМЕНИ

Следуя логике нащих с Вами, читатель, рассуждений, уравнения деформации описывают игру пространства и времени, забавляясь чередой обращений одного в другое. И если в механике сплощных сред трудно от- рещиться от материалистической основы этих забав, то в теории Максвелла те же самые уравнения описывают игру рафинированной Пустоты. В отсутствие зарядов:

Пусть в некоторый исходный момент существует

Естественно, что векторы Н магнитного поля меняются по тому же временному закону и вокруг hpix образуется вихревое электрическое поле в соответствии с первым уравнением. Совокупность силовых линий «новообразованного» электрического поля принадлежит набору тороидальных поверхностей.

Или, чтобы удобнее было изображать.

Здесь мы видим, что в исходной области пространства индуцированное поле, слагаясь с материнским, обращает его в ничто.

Вообще говоря, векторов индуцированного поля очень много, но если для любого сечения взять их проекции, так как любому вектору справа отыщется зеркально симметричный слева, то горизонтальные проекции в данном рисунке, суммируясь, обращаются в нуль. Аналогичная ситуация будет и в нижней части рисунка, хотя направления проекций имеют противоположный знак.

Вокруг каждого из них индуцируется вихревое магнитное поле, и совокупность вихрей делится на две группы. Одна вращается внутри кольца, а другая — в противоположную сторону снаружи. Уместно вспомнить, что ршен- но так, по разные сторош>1 поверхности, течет время. С одной стороны, из прошлого в будущее, а с другой — из будущего в прошлое (смотри предыдущий параграф). В плане чертежа, то есть в плоскости, перпендикулярной исходному току смещения, это вьплядит следующим образом.

Здесь видно, что на границе внутреннего и наружного вихрей суммарное электрическое поле обращается в нуль, но вновь возникает в центре вихря и еще дальще разбегается на периферии, меняя направление векторов напряженности. Поскольку периферия «разбежалась» весьма значительно, то говорить об обращении в нуль «горизонтальных» (по чертежу) компонент поля уже не приходится. И если считать направлением распространения поля радиальное раз- бегание в плоскости, перпендикулярной исходному току смещения, то следует задуматься о «поведении» продольных ^ I компонент поля. «Вертикальные» компоненты в центре рисунка при дальнейшей эволюции «повторят» прежнее: наружные «побегут» дальше. И можно предполагать: волна за волною.

Вихри вокруг «горизонтальных» компонент (обозначим убегание из плоскости чертежа от нас крестиком, а к нам — точкой) в совокупности образуют над всей «конструкцией» и под ней две группы силовых линий, имеющих одинаковое «направление» векторов напряженности.

В то же время внутренние совокупные вихри значительно ослабляются соседством двух противоположно направленных исходных вихрей. Поэтому результатом дальнейшей эволюции будет образование вихревого поля, охватывающего всю систему внутренних вихрей.

По сути дела мы вновь вернулись к замечательной интерпретации уникального геометрического объекта, выполненной С. В. Рудневым и вновь имеем систему сопряженных экваториальных торов.

Дело в том, что фронт волны, представляемый как поверхность постоянной фазы, должен и обладает свойствами поверхности. Для последней существует фундаментальный инвариант — полная кривизна. Или Гауссова кривизна, которая сохраняется при любых изгибаниях поверхности. Произведение двух нормальных кривизн (кривизны перпендикулярных сечений) остается неизменным. Для сферы эти кривизны одинаковы, и потому с «разбеганием» сферического волнового фронта они должны одинаково убывать. Поэтому и их произведение

Следует сразу же оговориться, что инвариант изгибания имеет место лишь для локального «куска» поверхности. Ко всей поверхности в целом его применить нельзя. Это хорошо видно на примере того же экваториального тора.

Конечно, было бы замечательно — вообразить, что поле в конечном итоге обращается в бесконечно тонкий шнур, свернутый в бесконечно длинное кольцо. И такая возможность, вероятно, существует.

В этом случае можно бьшо бы порассуждать об одномерном времени или приближении к одномерности. Если R стремится к бесконечности, то соответствующая кривизна — к нулю. Это значит, что деформация Пространства вдоль кольца несущественна и Время (всего лищь одна его шмпонента) не существует. Или не течет, если хотите. И, напротив, вторая компонента очень велика, так как при г —> О = (1/г) —> оо. Здесь время очень стремительно. Пренебрегая кривизной кольца (R —> оо, К, = (1/R) ^ 0) и рассматривая его отрезок как прямую (трубку? или фрагмент цилиндра Клиффорда) «линию», видно, что «линия времени» — это нечто вроде тоннеля. Выбраться из этого тоннеля трудно, поскольку деформация пространства в направлении (или г) весьма велика, а следовательно, велика и соответствующая энергия (точнее, сила, необходимая для преодоления пути вдоль г). Но зато вдоль «шнура» можно «перемещаться» с необыкновенной легкостью и невероятной скоростью, поскольку любая длина пути, деленная на «лениво» текущее (нулевое) время, дает очень большую величину, которую мы привыкли называть скоростью.

Образование бесконечно большого и одновременно бесконечно тонкого кольца — это всего лишь возможность. Напомним, в предыдущей главе мы уже рассматривали эту ситуацию относительно Поля и обсуждали частотный смысл кривизны. Поэтому более реальная ситуация — это образование стационарных структур Поля при эволюции его частот (кривизн). Можно по-прежнему рассматривать эволюцию как результат «перемножения» собственных частот (умножение векторов напряженностей поля), но можно, с другой стороны, и без эволюции. Дело в том, что деформации никогда не представляются строго синусоидальными, то есть строго ритмическими пропессами. Это связано с тем, что они конечны во времени или (и) в пространстве, что называется импульс. Существует изящный математический формализм Фурье, позволяющий разложить импульс на бесконечные и чистые ритмические компоненты. То есть такие, которые не ограничены ни в пространстве, ни во времени. Вечные. Сумма вечных компонент для каждого импульса своя, по каждой набор подчиняется очень простому правршу: ширина полосы частот обратно пропорциональна длительности его существования: AvAx > 1. В записанном виде это соотношение известно, в частности, как основное голографическое. Но, вероятно, это просто одно из самых фундаментальных основных соотношений. Например, если домножить левую и правую его части на постоянную Планка, то получим соотношение неопределенностей Гейзенберга для действия: hAvAx > h, но так как hAv = Е есть энергия, то АЕАх > h.

Но, впрочем, сейчас мы говорим не об этом. Наличие в импульсе множества компонент, которые распределены не только по частотам, но и по направленрмм распространения, приводит к тому, что всегда существует возможность выполнения в том или ином виде условий Лиссажу. А следовательно, по мере «расползания» импульса он «теряет» часть компонент и потенциала на образование стационарных структур. И только на заключительном этапе для самой низкочастотной компоненты, соответственно минимальной кривизны, реализуется нечто похожее на ситуацию с «раздвигающимся бубликом», что мы рассматривали выше.

Однако образование стационарных структур наподобие «шнуров» («шнуры» не кольцевой формы) происходит весьма часто. К сожалению, для описания структур поля (а соответственно, и геометрии времени) аналитические методы оказываются очень громоздкими и ненаглядными, т. е. трудно вообразить, как выглядят образы, описанные с помощью уравнений. Весьма кстати здесь оказывается компьютерное моделирование.

Упомянув Фурье-преобразование импульсов, трудно удержаться от еще одной возможности интерпретации, основанной на упоминавшейся ранее гипотезе тождества Пустоты и Света. Из нее прямо следует, что «вечные» компоненты )^е есть, а наши манипуляции сводятся лишь к перераспределению их. Мы как бы выхватываем фрагменты Поля из плена черноты деструктивной интерференции.

Говоря о геометрии Времени, мы должны помнить, что речь идет об эффектах электрического тока или, что то же самое, о магнитных полях. И, следовательно, о структуре (геометрии) вещества. О том, что вещество есть не что иное, как продукт времени (в буквальном смысле), говорил в свое время (опять каламбур) академик Н. А. Козырев.

«Вечные» компоненты Поля, скрытого Тьмой деструктивной интерференции, или, как сказали бы эзотерики, Света, съеденного Огнем, необязательно должны быть привычными нам по классической электродинамике бегущими волнами поперечного электромагнитного поля. Это может быть результат «модуляции» стоячих волн более общего свойства. Если допустить наличие волн деформаций Пустоты, распространяюпщхся со скоростями значительно большими известной скорости света, то их совокупность образует, естественно, систему стоячих волн. Вот об их модуляции и идет речь. В предьвдущей главе мы уже обсуждали возможность образования «медленно» бегущих волн из суперпозиции стоячих. К этому вопросу непосредственно примыкает и проблема взаимодействия структур Поля, то есть вещественных образований — Пустоты.

Пузыри в Пространстве (по Б. Н. Родимову) — суть частицы вещества. Это могут быть пузыри «растяжения»: пространство внутри разрежено, а снаружи уплотнено и пузыри «сжатия»: внутри пространство уплотнено, но разрежено снаружи. Отсюда соблазн войти вслед за Ацюковским в его газоподобный эфирный мир. Взаимодействия пузырей можно объяснить простыми эффектами давления. Но дело в том, что пузыри Родимова имеют динамическую природу. Они существуют только потому, что есть некоторый процесс, который удерживает пузыри от охлопывания или расползания. Как говорят физики, от релаксации. Этот «некоторый» процесс (насколько удалось показать, не знаю) есть эффект времени. То есть существование любой особенности Пространства, которая представляется даже совершенно стационарным объектом, есть результат суперпозиции нескольких колебательных процессов, то есть событий, связанных с преобразованием Пространства во Время и наоборот. Или, если будет более привычным, электрического поля — в магнитное, а магнитного — в электрическое. Для магнитных колебаний это, например, вращающаяся по орбите точка (или планета). Но в этом случае доступное наблюдению тело — это только часть событий, которые, кстати, развиваются и не так уж медленно. Движение планет — это как раз «медленный» результат сложения стоячих волн, образованных сложением достаточно стремительных волн.

Можно сказать, что это чушь, а причина заключена в наличии самой планеты и центростремительного тела — солнца. И спорить с этим невозможно. Просто это взгляд с другой стороны.

Быстрые процессы — это очень маленькие объемы. Примерно как атомы и элементарные частицы. Но это тоже суперпозиции колебаний. Высокочастотных колебаний. По сути дела любой вещественный объект — это пакет стоячих волн в соответствии с гипотезой де Бройля. Поэтому взаимодействие таких пакетов — это наложение одной группы стоячих волн на другую. Результат, как мы уже обсуждали в предыдущей главе, есть медленно бегущая несинусоидальная волна. Это и есть причина взаимодействий. Возникает движение частиц. Опять же описывать это аналитически — задача неблагодарная, и результат не очень наглядный. Здесь было бы удобно воспользоваться компьютерным моделированием, но в страницы текста это уже не впихнешь.

Скажем, с колебательными процессами, то бишь со стоячими волнами, понятно. Но как же с взаимодействием в стационарных полях? Дрейф частиц в этом случае подробно рассмотрен в классической электродинамике, куда автор и отсылает читателя.

Весьма велико искушение в заключение этой главы привести вывод материальных уравнений из собственно геометрических взаимоотношений для электромагнитного поля, зацепив при этом и гравитационные взаимодействия. Но доступного для изъяснения формализма у автора нет.

Глава 4.

В основе технологических решений, представленных в настоящей работе, лежат принципы голографической модели вещества, описанию которой посвящена отчасти последняя часть работы. Собственно голографическая модель является обобщением не только методологических решений общенаучного характера и опыта эволюции естественно-научной картины мира, но и, в значительной мере, опыта экспериментальной работы автора, многочисленных и разносторонних наблюдений структурных особенностей вещества различных уровней организации.

В работах, посвященных исследованию активных лазерных сред на кристаллах с центрами окраски, автором была выявлена недостаточность существующих модельных представлений для описания точечных дефектов F-типа. В то же время бьша обнаружена закономерность, описывающая спектр поглощения и люминесценции кристаллов галогенидов щелочей с центрами окраски. Эта закономерность содержала отношение целых чисел, что наводило на мысль о волновой природе центров окраски и, в частности, о гармоническом пакете волн, образующих пространственную конфигурацию типа фигур Лиссажу. Анализ электронно-микроскопических снимков различных материалов, включая цитологические препараты, убеждал в том, что наблюдаемые структуры есть не что иное, как интерференционные узоры разного рода. И так далее.

В экспериментах по синтезу метасиликатов кальция и магния и других материалов использованы представления голографической модели. Поскольку стабильное вещество представляется в ней гармоническим волновым пространственно-замкнутым пакетом, то процессы взаимодействия должны иметь резонансный характер. Конкретные механизмы установления резонанса могут описываться различными способами. Далее рассмотрен, например, хорошо известный в классической электродинамике резонанс в плазме и плазмоподобных средах.

и

rot Н = -£

5Е ° dt ■

rot Е = – ро —

Здесь 8q и Рр есть электрическая и магнитная постоянные. Приведенная запись уравнений Максвелла в дифференциальной форме допускает очень наглядную интерпретацию с помощью изображений силовых линий.

меняющееся во времени электрическое поле Е так, что дЕ ^ дЕ

— ^ О. — есть не что иное, как ток, в традиции на- dt dt

зываемый током смещения, в отличие от тока проводимости, существование которого обеспечивается наличием зарядов. Тогда второе из приведенных уравнений

описывает рождение вихревого магнитного поля Н.

9E/at#0

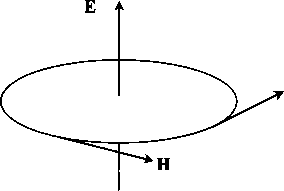
Рис. 3.2.1. Векторы Е и Н

дЕ/д1фО

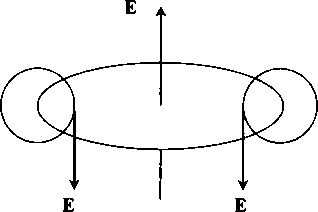
Рис. 3.2.2. Вихревое электрическое поле

Е А

к	>
> Е	f	> Е	г

Рис. 3.2.3. Вихревое электрическое поле (тор)

Л

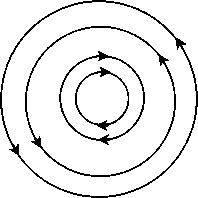
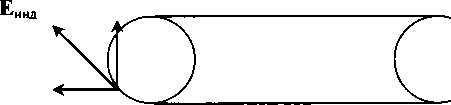
Рис. 3.2.4. Результирующие векторы индуцированного электрического поля

Итак, в центральной части «бублика» поле исчезло, оно как бы разбежалось в плоскости, перпендикулярной исходному электрическому полю. Теперь вьщелим одну из силовых линий и на ней два симметричных вектора.

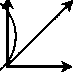
Е„

Рис. 3.2.5. Вихревое электрическое поле

Рис. 3.2.6. Вращение вихревого магнитного поля

Вокруг этих вихрей вновь индуцируются вихри электрического поля.

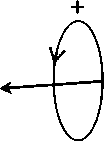
Рис. 3.2.8. Вихри вокруг «горизонтальных»

компонент

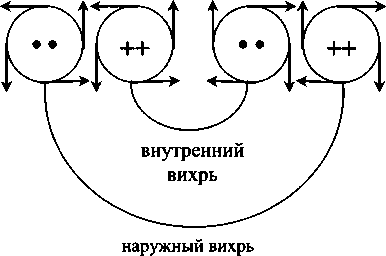
Рис. 3.2.7. Вихри индуцированного электрического поля

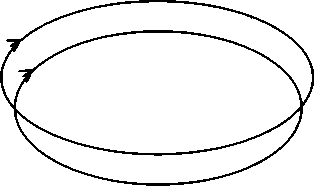
Рис. 3.2.9. Вихревое охватывающее поле

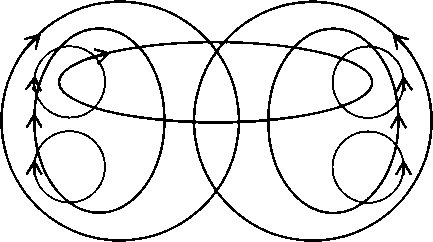
Рис. 3.2.10. Система сопряженных экваториальных торов

Достаточно очевидно, что графическое решение максвелловских уравнений имеет весьма косвенное отношение к классической теории распространения

электромагнитного поля. Раньше мы уже обсуждали произвол теоретиков, выкидывающих из рассмотрения возмущение, бетущее в одну сторону, оставляя второе. Мы и в данном случае могли бы получить подобный результат, если бы без всякого произвола рассматривали в «центре» системы источник тока смещения, который бы постоянно «пожирал» волну, бегущую в центр. Но и в этом случае весьма трудно представить классическую

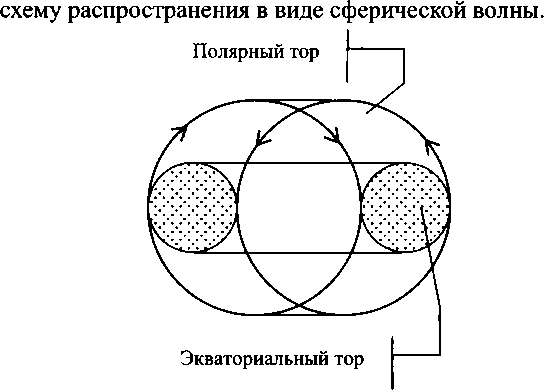
Рис. 3.2.11. Экваториальный и полярный торы

также будет убывать, что совершенно неприемлемо с геометрической точки зрения. Проблема снимается, если волновой фронт представлен поверхностью экваториального тора, так, что с уменьшением одной из кривизн (разбегание) происходит увеличение другой — в соответствии с инвариантом изгибания: К, • = const.

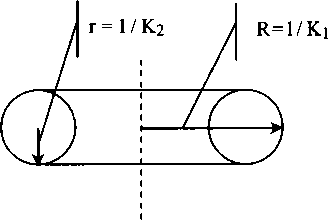
Рис. 3.2.12. Кривизны экваториального тора

СВЯЗЬ ВРЕМЕН

АНСАМБЛИ

РЕЗОНАНСЫ

Традиционная химия, основываясь на представлении о взаимодействии ионов как об интимном процессе, достигла замечательных успехов как в части фундаментальных результатов, так и, быть может, в большей степени, в решении задач практического материаловедения. Вместе с тем на пути детального поэтапного моделирования химических связей возникают существенные трудности в описании надатомных структур и соответствующих процессов. Одной из наиболее ярких проблем является, например, отсутствие адекватного представления о природе каталитических процессов, широко используемых в практике. Столь же практически значима необходимость понимания механизмов зольгельных процессов образования коллоидов и других надатомных структур в конденсированных средах.

Противоположным детальному описанию является широкое использование формализованных статистических приемов термодинамики, квантовой химии, а также достаточно новых научных направлений: неравновесной термодинамики, синергетики, макрокинетики и теории фракталов. Общим недостатком этих направлений, при несомненных достоинствах, является отсутствие достаточно наглядных образов физической картины описываемых явлений и процессов. В то же время формирование как общего мировоззрения, так и специальных дисциплинарных мировоззренческих представлений всегда опиралось на наглядные образы, как наиболее соответствующие реально наблюдаемому Порядку Вещей и Гармонии Мира в целом и деталях.

Целью настоящего раздела работы является попытка на качественном уровне представить физическую картину явлений, предшествующих химическому взаимодействию и во многом его определяющих.

Классическая кинетическая теория ансамбля частиц исходит из корпускулярных представлений и в силу этого основывается на гипотезе изотропного распределения частиц по скоростям в соответствии с равновероятностью всех направлений. В этой гипотезе нет каких-либо оснований для образования структуры, то есть каких-то форм порядка в ансамбле. Не возникает таких оснований и в квантовых распределениях Бозе-Эйн- щтейна и Ферми-Дирака, хотя последние и вовлекают в круг рассмотрения волновые свойства (функции) системы. Например, для фотонного газа с симметричной волновой функцией, заключенного в объеме V, соответствует распределение Бозе-Эйнштейна, описываемое гладкой функцией:

w = hv — энергия фотона;

h — постоянная Планка;

V — частота;

с — скорость света в вакууме;

к — постоянная Больцмана;

Т — температура.

Такое распределение по состояниям для фотонного газа в объеме V вступает в противоречие с результатами электродинамического рассмотрения, в котором существенным обстоятельством, определяющим распределение, является наличие замкнутого объема. Распределение справедливо лищь для очень большого объема. При малом объеме распределение деформируется собственными модами последнего и имеет вид, зависящий от интерференции электромагнитного поля. В связи с этим представление о фотонном газе имеет ограниченные возможности применения и, в какой-то мере, оправдывается лишъ при рассмотрении радиационного баланса на поверхности черного тела. Однако и здесь квантовая теория не является обобщением классической, а скорее есть ее следствие. Действительно, дискретность энергообмена между атомами, молекулами и ионами, определяемая выражением е = hv, является выражением известного из классической механики адиабатического инварианта — отношения энергии колебаний линейного осцршлятора к частоте при бесконечно медленном изменении параметров осциллятора:

Существенным достижением квантовой теории здесь является обобщение этого инварианта для широкого класса объектов, где const есть постоянная Планка. Условие же адиабатичности выполняется практически всегда, поскольку для объектов атомного масштаба даже в очень плотных средах время взаимодействия ~10’^с очень велико по сравнению с периодом изменения напряженности электромагнитного поля и равной ему характерной частотой самого осциллятора Ю с Гц).

Равновесное излучение в замкнутой полости соответствует установившемуся режиму электромагнитного поля, и его нельзя рассматривать как совокупность плоских элементарных некогерентных волн. Объемная плотность энергии поля черного излученР1я существенным образом зависит не только от температуры, но и от формы, размеров и материала стенок полости. Распределение объемной плотности энергии в сферической полости, например, может быть найдено как решение уравнения Лапласа в сферических координатах с заданными краевыми условиями. Это так называемые сферические гармоники, описывающие в случае электромагнитного поля совокупность стоячих волн. Частота самой низкочастотной волны (моды) определяется размером полости и не может быть ниже = с / (2Д) где с — скорость света, а Д — диаметр полости. Верхняя частота определяется свойствами стенок полости. Для идеально проводящей поверхности где

где n — концентрация; e — заряд; m — масса частиц.

Для металлов при концентрации электронов п ~1(F^ см”^ частота имеет порядок 10’* Гц, и они прозрачны для более высоких частот, то есть радиационный баланс места не имеет и поле соответствующей частоты в замкнутой полости находится в равновесии с внешним полем. В классической модели невзаимодействующих радиационных осцилляторов наличие высоких частот приводит к так называемой «ультрафиолетовой катастрофе», связанной с тем, что спектральная плотность энергии поля монотонно растет с ростом частоты, а интегральная энергия поля обращается в бесконечность, что явно противоречит опыту. В то же время собственные моды электромагнитного поля резонатора (замкнутой полости) не аддитивны по энергии и в рамках классических представлений не приводят к бесконечным величинам. Энергия поля в бесконечно малом объеме является квадратичной функцией его напряженности: dW = (Е^ + Н^) dV, в свою очередь, напряженность поля в этом объеме является суперпозицией напряженностей частных компонент поля. Суперпозиция отлична от нуля толъко для не слишком больших мод. В области высоких частот в изотропном поле со случайными фазами колебаний с)ПУ1мирование большого числа равновероятно распределенных напряженностей дает нулевой результат, математически строго следующий из Фурье-анализа. Таким образом, энергетический спектр равновесного поля обусловлен его низкочастотной частью, причем даже в том случае.

Оговорка, сделанная выше по поводу слабости взаимодействия между частицами и полем, существенна в том смысле, что при сильном взаимодействии в электромагнитном поле возникают новые моды, и структура его уже не может описываться только распределением собственных мод. Более того, наличие ограничивающей объем поверхности, даже не обладающей сколько-нибудь заметной проводимостью, вызывает образование так называемых поверхностных плазмонов. В результате структура поля вблизи поверхности оказывается промодулированной еще и ими.

Прежде чем продолжить анализ канонических распределений уже в отношении ансамблей из частиц с антисимметричными волновыми функциями, вернемся к «безэнергетической» высокочастотной части «черного» излучения. Сам по себе прижившийся в научном обиходе термин «черное излучение», как жаргон, обозначающий излучение черного тела, по существу является очень точным, несмотря на некоторую каламбур- ность. Действительно, наличие спектрально плотного высокочастотного электромагнитного поля при всей его реальности никак не проявляется в известной физической практике. Совершенно безразлично пока для нас, существуют ли низкочастотные поля в «пустом» пространстве или эти низкочастотные поля являются всего лишь биениями «черного» излучения. Однако уже в самой реальности Фурье-разложения импульсов электромагнитного поля конечной продолжительности по гармоническим, то есть бесконечным «вечным» составляющим, содержится, по крайней мере, формальная возможность существования непроявлен- ного («черного») излучения. Формализм Фурье-разложения строг и реален, что подтверждено экспериментальной практикой в совершенно разных областях физики. Если этот формализм реален и физически, то возникают существенные гносеологические следствия типа тождества пространства и света, «иллюзорности» вещества и многие другие достаточно нетривиальные для современного научного мировоззрения проблемы. Но в любом случае воспринимаемая нами реальность — это в той или иной мере конструктивная интерференция в низкочастотном спектре излучения и деструктивная — в высокочастотном. Независимо от того, первично ли это излучение или является результатом биений высокочастотного «черного излучения».

Процессы образования структуры какого-либо рода в ансамбле частиц так или иначе связаны с электромагнитным полем, которое в веществе существенно отличается от поля в вакууме. Это связано с возникновением продольных колебаний, то есть таких, в которых смещение частиц среды имеет компоненту, параллельную вектору распространения поля. Взаимодействие частиц с полем сводится к тому, что они получают энергию от поля и отдают ее ему. Во многих случаях это сбалансированный процесс, и количество полученной энергии равно количеству возвращенной. Ситуация, однако, осложняется наличием у вещества собственных резонансных частот.

Рассмотрим ансамбль одинаковых частиц с электрическим зарядом. Размеры ансамбля для нас пока несущественны. При концентрации частиц п (шт.) / см^ одна частица занимает объем порядка ~ 1 / п. Благодаря кулоновскому взаимодействию (отталкивание для частиц одинакового заряда) частица находится в «центре» занимаемого объема. Сила, удерживающая частицу,

Отсюда жесткость взаимодействия К:

Определим амплитуду А колебаний выделенного электрона и сравним ее с характерным размером элементарного объема V^. Энергия осциллятора = шА^со^ / 2 может быть определена как W = кТ, где к — постоянная Больцмана, Т — температура. Если взять последнюю равной характеристической = hv / к ~ 10 000 К для электронов в металле, где п ~ 10^^ см ^ со ~ 10’’с ‘, что соответствует нулевым, то есть неустранимым колебаниям, то из равенства

Определим концентрацию частиц в ансамбле, для которой непосредственно справедлива статичная модель собственного резонанса. В этом случае следует полагать, что удвоенная амплитуда резонансных колебаний никак не больще линейного размера «элементарного объема», то есть

Из энергии «нулевых» колебаний ищем амплитуду: hv = mA^co 2

Для «свободного» электронного газа при массе частицы = 9,1 X 10’^’ кг п < 7,6 X 10^® м’^, то есть «элементарный» объем составляет величину V ^ ~ 0,13 х 10″^® м^ с амплитудой свободных нулевых колебаний А = 0,26 х 10 ‘® м при резонансной частоте

Ур^ = со/(2я)= 1,43 X Ю’^Гц. Концентрация «свободного» протонного газа (т = 1,67 X 10’^^ кг)

Видно, что амплитуда колебаний протона близка к характерным ядерным размерам ~ 1,5 х 10 ‘^ м, в то время как амплитуда электрона соответствует атомному размеру, хотя взаимодействие протон — электрон в данной модели не учитывается. Можно также рассмотреть газ из протонно-нейтронных пар, считая их находящимися в жесткой сцепке. Вследствие удвоения массы по сравнению с протоном концентрация такого газа Пр^ < 8Пр < 3,8 X м \ что примерно на три порядка меньше известного из опыта значения для ядра, амплитуда колебаний пары А^^ ~ 0,7 х 10 ”* м при резонансной частоте v ~ 5,25 х 10” Гц.

Рассмотрим еще одно модельное приближение, имеющее отношение к плазменному резонансу. Пусть ансамбль частиц представлен смесью «свободных» электронов и протонов, взятых в равных количествах, то есть = Np. В этом случае на «вьщеленный» электрон действует и электронное, и протонное окружение, но в противоположных направленрмх. С большой степенью точности можно считать это интегральное взаимодействие нулевым, если исключить из рассмотрения протон, находящийся в «выделенном» электронном объеме. Тогда сила, «возвращающая» электрон, определяется только этим протоном:

Полученные результаты соответствуют абсолютно уединенной паре протон — электрон. В реальных условиях на колебания частиц будет накладываться реак- ЦР1Я среды, обусловленная излучением и поглощением на частотах резонанса. Длины волн, соответствующие этим частотам: v ^ = те’* / (16eg^h^) равны X, = с / v или X = 168p^chV (me’*).

Произведение X m является инвариантом L = X m = 168^chVo’*. ОтсюдаX = L/m = 1,8 х 10’м

Тем не менее подчеркнем, что и в данной модели, несмотря на погрешности, сохраняются некоторые совпадения. Так, хотя амплитуда «свободного» электрона больше реальной в атоме в два раза, но также в два раза больше радиуса атома длина волны протонного резонанса.

При исследовании рассматриваемых вьппе моделей ансамблей частиц мы часто употребляли термин «колебание». Однако его корректное использоваьше может быть оправданным только в случае одномерной модели, то есть когда движение осуществляется вдоль некоторой оси. Такая модель вовсе не применима при описании электронно-протонной пары, поскольку в области локализации протона сила взаимодействия становится неопределенно большой, а физическая картина—достаточно бессмысленной. Электрон падает на протон. На самом деле этого не происходит. Уже в двумерной модели «свободного» электронного газа или уединенной пары в силу центральной симметричности взаимодействия электрон движется по круговой замкнутой траектории. Формально такое движение можно разложить на два ортогональных колебания, не умаляя применимости понятий теории колебаний. В этом случае возникает естественное распределение частиц по скоростям: от нулевой до вполне определенной максимальной, соответствующей тангенциальной скорости частиц.

На самом деле это просто формализм. Более корректным могло бы быть распределение именно по тангенциальным скоростям либо по модулю скорости. Однако в идеальном равновесном ансамбле скорости одинаковы по модулю. Более того, в таком ансамбле частицы, в принципе, могут совершать только синфазное или антифазное движение. Последнее утверждение теории колебаний для равновесного ансамбля осцилляторов требует некоторого уточнения. Дело в том, что при концентрациях частиц, соответствующих реальному веществу, и при разумных температурах амплитуда колебаний несколько, а иногда значительно, превышает линейные размеры «элементарного» объема. Это, как указывалось выше, приводит к физически бессмысленным бесконечным силам взаимодействия в случае анти- фазного движения. Можно предположить, что частицы ансамбля участвуют только в когерентном (синфазном) движении, никогда не сближаясь «вплотную» друг с другом. В этом случае у ансамбля должен быть отличный от нуля суммарный момент импульса, что имеет место далеко не всегда. Следовательно, в ансамбле присутствует в равной мере как синфазное, так и антифазное вращение частиц.

Если исключить из рассмотрения поле, изменяющееся с частотой плазменного резонанса и имеющее характерную длину волны, значительно превышающую амплиту-

Такая ситуащм возможна только в ансамбле сильно связанных пар частиц типа электрон — протон, когда размер орбиты электрона контролируется в основном резонансом протона, точнее, длиной волны соответствующего поля. Для внешних электронов более тяжелых атомов заряд ядра в значительной мере экранирован, и влиянием электронного резонанса пренебрегать уже нельзя.

Конфигурации структур ближнего порядка, разумеется, не исчерпываются приведенными на рисунке

dn (w) = dq / 1),

где dq — полное число состояний в объеме V,

V 2

dq = 8я W dw;

W / © = const.

осц

частота является важной характеристикой любого вещества, имеющей смысл частоты резонанса наиболее легких частиц в плазмоподобной среде. Плазменная частота определяется из выражения:

2TiVp = (ne^/

когда выделенный объем очень велик. Размеры объема, ограниченного поверхностью с конечной проводимостью, влияют на форму кривой распределения спектральной плотности энергии. При больших размерах она приближается к гладкой классической. При малых обладает максимумами и минимумами, соответствующими в равновесном случае распределению интенсивностей в поле стоячих электромагнитных волн. Это обстоятельство имеет для нашего рассмотрения достаточно важное значение, поскольку структура стоячих волн может быть «продекорирована» ансамблем слабо взаимодействующих между собой и полем частиц. Действительно, такие частицы будут «выметаться» давлением электромагнитного поля из пучностей, где вектор Пойнтинга максимален, в узловые области, что фактически означает образование вещественной структуры, существенным образом зависящей от формы и размеров «реакционного» сосуда. Причем в значительном большинстве случаев могут быть созданы такие напряженности поля, что силы межчастичного взаимодействия будут сравнимы или даже малы по сравнению с силами, действующими на частицы со стороны поля, то есть образование собственно вещественных структур будет подчинено структуре поля.

Р = еЕ = ерг/(Зб(,),

е — заряд частицы, р — объемная плотностъ заряда ансамбля, г — расстояние частицы от центра элементарного объема, Sq — диэлектрическая проницае- мостъ вакуума, Е — напряженность поля, записанная в предположении равномерного распределения заряда по ансамблю большого числа частиц, имеющего форму шара.

р = Ne / V = пе,

N — число частиц в ансамбле;

V — объем;

п — концентрация зарядов.

K = dF/dr = neV(3e„)

и резонансная частота собственных колебаний частицы массой m около «выделенного центра»:

= К / m = neV (Зе^т)

совпадает с точностью до множителя 1/3 с выражением для плазменного резонанса.

hv = кТ = mAW/ 2

С

получаем

А^ = 2hv / (mco^) = 2h / (шясо) ~ 10’’ м^,

откуда

А~3 X Ю’^’м,

с другой стороны, характерный размер элементарного объема при указанной концентрации п ~ 10^’ м‘^

R~(l /п)‘’з~2,15 X 10 ‘Ом.

Близость значений R и А, причем А > R/2 почти в три раза, физически означает для рассмотренной статичной модели обращения в бесконечность возвращающей силы вблизи «стенки» выделенного объема. Картины не меняет и учет дебаевского экранирования заряда. Для электронов в металле радиус дебаевского экранирования составляет величину порядка Гд ~ 10 ’ м, а следовательно, «выделенный» электрон в центре дебаевской «области» взаимодействует по крайней мере с десятью тысячами соседей, поле которых не экранировано. Таким образом, статичная модель, а вместе с ней предположение о равновероятном (случайном) распределении скоростей частиц в ансамбле, несмотря на корректность количественного результата, подтверждаемого экспериментальными данными, приводит к бессмысленной физической картине. Можно предположить, что проблема заключается в невозможности применения механической модели частицы. И это предположение, скорее всего, верно. Однако ограничений на механическую модель со стороны квантовой механики нет, поскольку там характерный размер, требующий учета волновых свойств частицы, определяется комптоновской длиной волны электрона;

X = h / (m^c) ~ 2,4 X 10-12 м,

которая на два порядка меньше как амплитуды колебаний, так и линейных размеров «элементарного объема».

2A<(VJ*’2 = 1 / (п”2).

р р

или, так как ю = 2яу, со^ = пе^/ (вдШ^), получаем А” = с/п, где с = ЗЬ^8ц / (я^е^ш). Далее из условия для амплитуд находим

2(с / < 1 /

или 2‘^с^п < 1 и, окончательно, п < (т / (Зе^))^ (ея / (4h))*.

п<4,73х 10^мЛ

а амплитуда колебаний протона А ~ 1,8 х 10 ‘^ м при резонансной частоте

V ~2,63х 10’’Гц.

рп ’ ^

~ еЧяе/,

где г — по-прежнему расстояние между протоном и электроном, соответствующее амплитуде «нулевых» колебаний последнего. Упругость взаимодействия K = dF/dr = eV(27t8/).

= (eV (2я8/т^))‘’1

Тогда, и так как ~ W^l 8=1/ (8пе), получаем выражение плазменного резонанса:

Юре = (4е^Пе/ (Я8„те))’^^

ИЛИ, поскольку г = А,

“ре = (2яеДЗте))’^^.

Из энергии колебаний находим

ЬЮр/ (2я) = шА^Юр^/ 2,

или

h = яАе^т (е^/ (2Я8дАе^П1е))‘^^.

Отсюда получаем

АеШе = (яе^).

Амплитуда колебаний электрона в нашей модели:

А ~ 1 X Ю ‘^ м,

е ’

что примерно в четыре раза больше радиуса атома водорода. Очевидно, что так же может быть определена и амплитуда колебаний протона:

А ~А / 1836 « 0,6 X Ю-’^м.

рез о *^6 рез е ’

и Хр ре^ = L / Юр = 1 X Ю’*** м. Порядки полученных величин соответствуют надатомным масштабам, и, в связи со свойствами электромагнитных резонансных систем, собственные резонансы могут явиться причиной структурирования вещества безотносительно к условиям ближнего порядка, то есть в над атомной и надмолекулярной иерархии. Используя модель смеси, определим ее плотность, полагая, что она соответствует плотности водорода при температуре вблизи о К. Так как р – Sm / V, где Zm = N (m^ + Шр), а V = ~ N8A^ то р » (т^ + Шр) / (8А^^), и так

как Шр, то р ~ Шр / (8А^^). Откуда р ~ 165 кг/м^,

что примерно вдвое больше реально наблюдаемой (72 кг/м^), и свидетельствует о том, что модель уединенной пары не вполне корректна.

Таблица 4.1

Сводная таблица параметров резонансов

	Газ электронов	Газ протонов	Пара электрон — протон	Газ протон — нейтрон
Максимальная концентрация (м^)	7,6 X Ю’о	4,7 X Ю-”»	1 X 103»	3,8 X 10^’
Амплитуда колебаний (м), электрон протон	0,26 X 10-‘о	1,8 X Ю-‘з	0,6 X ю ”	0,2 X 10 >‘’
Резонансная частота (Гц) электронная протонная	1,43 X 10 *‘	2,63 X 10”	1.6Х lOli 3 X 10‘«	5,27 X 10”
Длина волны, соответствующая резонансу (м)	2,1 X 10-«	1,14 X 10-“	1.87 X 10=2 1 X 10->»	5,7 X Ю-‘з

ду колебаний (или, что то же, радиус орбиты вращения в двумерной модели), то ансамбль с нулевым интегральным моментом импульса представить не сложно. Орбиты отдельных частиц, «соприкасаясь», образуют упорядоченную решетку, как показано на рисунке 4.1.1.

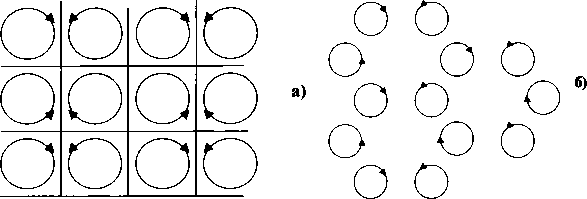
Рис. 4.1.1. Движение частиц ансамбля

Более того, напомним, что мы рассматриваем пока только двз’мерную модель движения частиц. С другой стороны, может оказаться предпочтительным в определенных условиях синфазное движение внешних электронов ближайшей пары, как это происходит в молекулах. Конденсат из таких молекул, вероятно, вновь образует структуру, подобную рассмотренной, но на каждой «орбите» будет уже по паре электронов.

Трехмерное движение частиц ансамбля, как плоское по двум, удовлетворяет разложению по трем нор

мальным колебаниям, но по-прежнему это справедливо лишь для проекций «траекторий» частиц. На самом деле частицы движутся, как и в плоской модели, по замкнутым траекториям, но «плоскости» этих траекторий «качаются» таким образом, что оси, проведенные через центральную точку, перпендикулярно плоскости, описывают конические поверхности. Устойчивые структуры ансамблей образуются не только при единственной резонансной частоте, когда все нормальные частоты одинаковы, но и в том случае, когда между нормальными частотами существуют кратные соотношения. Условия образования устойчивых структур ближнего порядка соответствуют условиям возникновения фигур Лиссажу. Может возникнуть вопрос: какое отношение имеет модель из классических «точечных» частиц к рассматриваемой далее голографической модели вещества? На первый взгляд — никакого. Однако определенное соответствие между ними просто обязано быть. И оно состоит в том, что «траектория» классического электрона формой и размерами соответствует той самой фигуре Лиссажу, которая есть результат автоинтерференции исходной электромагнитной волны. Образование фиг)ф Лиссажу есть прямой аналог процессов образования стационарного электромагнитного объекта-частицы. В случае пересечения фронтов внещних полей образуются виртуальные частицы, а при определенных условиях — реальные. Впрочем, форма последних не вполне круговая, а соответствует геодезической линии поверхности тора. Анализ соответствия траектории классической частицы голограмме показывает и корректность понятий «распределение электронной плотности», «плотность вероятности» и т. п. Действи

тельно, и масса, и заряд «частицы» «размазаны» вдоль контура, образованного конструктивной интерференцией соответствующего замкнутого поля.

Перейдем теперь к оценке размеров ансамбля частиц из условий «плазменного» резонанса, полагая, что в «бесконечной» среде в равновесном состоянии устанавливаются стационарные колебанР1я, соответствующие стоячим волнам. Длины последних можно определить из резонансных частот, и основные из них приведены в таблице 4.1. Следует напомнить, однако, о некорректности рассматриваемых моделей. Дело в том, что в них учитываются упругие взаимодействия, обусловленные только кулоновскими силами. Но ввиду того, что многочастичные ансамбли прш1ципиально нестатичны, соверщенно необходим учет и магнитных взаимодействий, то есть в формулах для определения собственных частот должна фигурировать сила Лоренца. Неучет этого обстоятельства приводит к значительному, на три порядка, расхо- жденрпо с реальным значением плотности ядерного вещества. Вместе с тем порядок плотности электронного газа и газа электронно-протонных пар близок к реальной, что указывает на малость магнитного вклада в атомных взаимодействиях. Поэтому ради простоты подхода в дальнейшем не будут рассматриваться внутриядерные резонансы. Отметим лищь то, что эти резонансы необходимы для существования самого атома и гармоничным образом «зависят» от комптоновской частоты электрона, то есть от его массы. В противном случае атом как колебательная система имел бы очень непродолжительное время жизни.

При оценке размеров ансамбля частиц мы допустим еще одну «вольность», связанную с неучетом диспер-

сии электромагнитных волн в веществе, полагая их ско- рость близкой к скорости в вакууме.

Для электронейтральной смеси электронов и протонов, что соответствует «жидкости» из атомов водорода, поскольку расчет производился только для нулевых колебаний, имеются две характерные частоты электронно-протонного резонанса, приведенные в таблице 4.1. Кроме того, существуют две парциальные частоты для электронной и протонной компонент смеси. Их значения в соответствии с выражением для максимальной концентрации смеси: п = 10^’^ м’^ равен v = 5,2 х 10*^ Гц, = 1,21 X Ю*’* Гц. Четырем указанным резонансным частотам соответствует самосогласованное поле стоячих волн с длинами X = с / V. Для нас важны расстоянрм между узловыми поверхностями, равные А. / 2, в пределах которых фаза колебаний частиц под воздействием поля соответствующей частоты остается неизменной. Эти расстояния приведены в таблице 4.2.

Таблица 4.2

Расстояния между узловыми поверхностями

Номер полосы «частот»

1

2

3

4

Частота резонанса (Гц)

3 X 10‘*

5,2 X 10’*

1,6 X 10’5

1,2 X 10’“

Длина полуволны (А)

0,5

2,9 X 10^

0,94 X 10^

1,25 X 10“

Наиболее коротковолновая компонента резонансного поля образует структуру из пучностей и узловых поверхностей с периодом ровно в четыре раза меньщим поперечного размера «орбиты» электрона. Это означает, что последняя существенно отличается от круговой, так как модулируется высокочастотным полем ядра. Ясно вместе с тем, что это явления атомного и субатомного порядка, а в более сложных моделях — молекулярного.

Помимо четырех основных резонансных частот, в спектре поля присутствуют интеркомбинационные компоненты, представленные разностными частотами. В результате основные компоненты «размываются». Для коротковолновой компоненты это размытие мало и составляет доли процента. Действительно, максимальная разность частот Ду = 5,2 х 10*^ Гц при значении основной частоты v = 3 х 10’* Гц. На рисунке 4.1.2 представлен интеркомбинационный спектр частоты ~ 3 X 10’* Гц.

По сути дела, в «атомном» спектре представлены все резонансные частоты, обусловленные кооперативными (ансамблевыми) взаимоотношениями частиц.

Структура поля, обусловленная второй частотой с V = 5,2 X 10’^ Гц, также образована из пучностей и узловых поверхностей, следующих друг за другом с периодом 2,9 X 10^ В пределах этой пучности могло бы уместиться около нескольких миллионов атомов, т. к. N ~ ((А, / 2) / 2А)*, где А — амплитуда электрона. Но эта структура поля весьма неопределенна, поскольку ее основная частота сильно «размыта» интеркомбинационным взаимодействием. Спектр частоты 2 представлен на рисунке 4.1.3.

Рис. 4.1.3. Спектр второй резонансной полосы

В результате такого «размытия» частицы ансамбля не в состоянии занять устойчивое положение и как вещественная струюура поле проявляется редко, но эта же особенность его существенна для характера движения частиц ансамбля, что будет обсуждаться несколько позже.

Третья резонансная частота также имеет структуру, обусловленную интеркомбинационным взаимодействием с четвертым резонансом. Однако ее уширение не превышает десяти процентов, которое можно рассматривать как модуляцию, не влияющую на образование стоячих волн. Размер пучности определяет размер ансамбля частиц, совершающих когерентное движение в ее пределах под воздействием резонансного поля. Несмотря на явную приблизительность рассматриваемой модели ансамбля, надатомные структуры с размерами порядка 100 нм встречаются в самых разных материалах достаточно часто, даже тогда, когда не приходится говорить о состояниях ближнего порядка или признаках кристаллизации. Чаще всего речь идет о коллоидных или золь-гельных системах. Следуя логике нашего анализа, коллоиды являются весьма общим свойством любой жидкости, находящейся в равновесном состоя-

НИИ. Далее, если внутри коллоидного микроансамбля устанавливаются высшие резонансы, то он приобретает свойства стабильного химического соединения, вплоть до образования конденсированной твердой фазы. Это явление широко наблюдается при массовой кристаллизации из растворов, с характерными размерами выпадающих частиц около 100 нм. В случае отсутствия устойчивых высших резонансов коллоидная или гелеподобная структура жидкости может легко разрушаться при внешнем воздействии, например, при встряхивании, освещении или иным образом. Склонность к разрушению гелей при внешних воздействиях обусловлена тем, что при наличии внешних факторов структура стоячих волн превращается в континуум бегущих, и вслед за тем исчезает и вещественная структура.

Напряженность поля стоячих волн зависит главным образом от природы образующих среду атомов, которые, естественно, сильно отличаются от рассматриваемой модели электронно-протонной пары. Поэтому в спектре может доминировать как третья, так и вторая частота. Но примечательно то, что в реальности встречаются коллоиды с размерами именно порядка 30- 100 нм. Еще более широкое распространение имеют ансамбли с размерами, отвечающими четвертой резонансной частоте, то есть порядка одного микрометра. В этот диапазон попадает большинство клеточных образований в биологических объектах и огромное число минеральных индивидов. Очень характерным является широко используемый в химической технологии процесс созревания осадка, который первоначально представлен обычно частицами с размерами около одной десятой микрометра и создает сложности при фильтрации. В процессе созревания образуются агрегаты с размерами более одного микрометра, которые проще отфильтровывать.

Рассмотрим вкратце характер движения частиц в резонансном микроансамбле. В целом оно подобно рассмотренному выше движению электрона, описывающего в трехмерном варианте поверхность полярного тора, принадлежа в то же время замкнутому плоскому контуру. Но есть и существенное отличие в том, что напряженность поля в центре пучности достигает максимума, а следовательно, именно в центре на частицы действуют максимальные силы со стороны поля. В соответствии с этим, также в центре пучности максимальны ускорения и скорости частиц, то есть в микроансамбле существует некоторый градиент угловых скоростей. В этом случае когерентность движения может сохраняться лищь при движении частиц по поверхности экваториального тора. Плоскость его большого сечения, в свою очередь, может качаться таким образом, что главная ось тора описывает коническую поверхность. Мицеллы в форме экваториальных торов встречаются довольно часто, хотя и значительно реже, чем образования в виде полярных торов. Дело в том, что центральная часть пучности испытывает существенное дебаевское экранирование и развитие экваториальной структуры реально лищь для ансамблей второй резонансной частоты (30 нм) и реже — третьей (~ 100 нм). Экранирование приводит к тому, что доминантным является формирование оболочечной структуры с размерами порядка одного микрометра, поверхность которой приобретает важное значение для резонансного электромагнитного поля. То есть наряду с формированием объемных плазмонов возникают условия для существования поверхностных.

Из электродинамики известно, что резонансные частоты поверхностных плазмонов определяются все тем же плазменным резонансом, но меньше частот объемных плазмонов ровно в 2’^^ раза. Следует отметить, что между фундаментальными характеристиками среды, такими как резонансные плазменные частоты и радиус (размер области) дебаевского экранирования, существует принципиальное родство, поскольку обе они являются функциями плотности электрического заряда. Действительно, формулы для них в системе СГС:

(0| = (4яе^п / т)‘’^ и

Геометрия электромагнитного поля с участием поверхностных плазмонов требует специального исследования, и здесь мы ограничимся лишь тем, что в резонансном спектре появляются дополнительные частоты, влияющие на структуру среды, преимущественно в диапазоне размеров микрообластей порядка микрометра.

Можно продолжить анализ структуры равновесной среды, взяв за отправную точку уже не электроны и протоны, а их микроансамбли. В этом случае возникает ряд иерархически связанных структур миллиметрового и метрового диапазонов и далее, вплоть до иерархии космических структур. Но и этот анализ не входит в задачи нашей работы, хотя раскрывает механизмы Вселенской красоты и гармонии.

Обратимся к анализу высших резонансов, определяющих внутреннюю структуру плазмонов. Как мы выяснили ранее, электронные резонансы определяют предел плотности конденсированной среды из атомоподобных частиц и именно они в равновесных условиях являются высшими, составляя порядки 10’^-10‘® Гц. Говоря другими словами, электронные резонансы контролируют размеры объектов атомного масштаба. Можно утверждать, что атом в разреженной среде больше того же атома в конденсированном веществе. Использованные модельные представления показывают, однако, что для одноэлектронных частиц диапазон вариации объема не столь уж и велик. Так, для максимальной плотности среды амплитуда электрона порядка 0,26 х 10 ‘® м (таблица 4.1), а для «свободного» атома ~ 10 ‘“ м. Естественно, что вариация плотности среды должна оказывать влияние на положение резонансных полос. Это и на самом деле имеет место, хотя и в меньшем масштабе.

Реальная среда, конечно же, не описывается простыми моделями, хотя бы потому, что состоит из многоэлектронных атомов с тяжелыми ядрами, обладающими к тому же не единичным зарядом. Тем не менее, концентрация частиц в конденсированных средах будет определяться именно электронными резонансами. С другой стороны, взаимоотношения атомов в пределах плазменного микроансамбля зависят от частот парциальных резонансов ядер, поскольку легкие и «быстрые» электроны адиабатически подстраиваются под движения ядер. То есть, несмотря на то, что взаимодействия ионов формально могут быть сведены к электростатическому, обменному и т. п., их реакционная способность зависит прежде всего от наличия общих частот или их совпадающих гармоник. Тем самым химизм процессов определяется не только индивидуальными свойствами взаимодействующих атомов, но и кооперативным влР1я- нием среды и, естественно, термодинамическими условиями, которые, в принципе, относятся исключительно к описанию ансамбля.

Рассмотрим наиболее простой случай, реализующийся при наличии общих частот. Парциальные резонансы для атомов i-ro и к-го сортов с зарядом ядра Z. и Z^:

©. = (nZ.^e^/ Щ;)‘^^,

и

отсюда при известных т^, т. и Z., Z^

n.Z.^ / m. =

и равном количестве взаимодействующих ионов N. = элементарный объем, приходящийся на одну частицу, пропорционален ее массе, так как п = N/V или V^=l/n = V/N. Отсюда, поскольку ~ то

есть элементарный объем пропорционален кубу ионного радиуса, на соотнощения последних в бинарных молекулах накладывается условие:

r.3m./Z.2=rX/Z2

Возможен также случай структуры для ионов с сильно отличающейся массой и зарядом ядра, когда cOj = 2о)^^. Для бинарного соединения здесь получаем:

4r.3m./Z.2=r,X/Z2

Часто удобнее, однако, пользоваться выражением для частот, связывающим не ионные радиусы, а парциальные концентрации частиц.

Для среды из многих типов частиц условие гармо- низма выражается в том, что могут быть реализованы любые линейные комбинации парциальных ядерных частот ^ (Оу = О.

Полученные выражения справедливы для ансамблей с размерами порядка 30 нм. Для выяснения ближнего атомно-молекулярного порядка необходимо привлечение моделей, отличающихся от рассмотренных. Дело в том, что структура ансамбля зависит, конечно же, не только от парциальных ядерных частот, но и от электронно-ядерных резонансов. К примеру, атом с двумя спаренными электронами (гелий) таких резонансов вообще не имеет, поскольку в этом случае возвращающая сила, действующая на ядро со стороны электронов, всегда равна нулю, за исключением ситуации, когда атом находится в сильном внещнем поле. Поэтому CTpyiaypa «жидкости» из таких атомов определяется в основном парциальным резонансом ядер, хотя иногда, например, в электрическом разряде, возможно образование эксимерных молекул. В этом смысле на ближний порядок основное влияние оказывают электроны внешней атомной оболочки, которые благодаря асимметрии в плотности электрического заряда обеспечивают наличие возвращающей силы, действующей на ядро, и тем самым существование собственного электронно-ядерного резонанса.

Ситуация, подобная атому гелрм, когда возвращающая сила электрона попарно компенсируется другим электроном, находящимся с другой стороны ядра, характерна для всех благородных газов. Естественно, отсутствие электронно-ядерного резонанса не определяется наличием четного количества электронов у атома, поскольку конфигурация их распределения, за счет кулоновского взаимодействия, не всегда соответствует антифазному колебательному движению. Например, у атома бария четыре электрона, и если рассматривать только кулоновское взаимодействие, то они должны образовывать тетраэдрическую конфигурацию, в которой строго антифазное движение невозможно. На самом деле мы должны напомнить, что электрон — не вполне частица, но даже при таком «частичном» представлении следует учитывать, вообще говоря, силу Лоренца, а не Кулона. Можно было бы продолжить рассмотрение резонансов атомов, ионов и молекул на предложенной основе. Но это не входит в нашу задачу: выявление тех особенностей среды, которые не учитываются химией. Формализм квантовой химии, восходящий к тем же самым резонансам, вполне продуктивен. Мы же хотели подчеркнуть кооперативные особенности среды из заряженных частиц.

Обсуждая тему высших резонансов в ансамбле частиц, которые определяют ближний порядок, то есть ответственны за молекулярные связи, подчеркнем следующее: для длительного, то есть стабильного, существования ансамбля требование равенства частот должно выполняться для всех частот ансамбля, включая самые высшие и самые низшие моды. Это требование стабильности имеет универсальный характер и справедливо в том числе и для волновых пакетов. В противном случае, когда

может быть определено время жизни ансамбля из адиабатического инварианта или эквивалентных ему соотношений неопределенности, либо основного голографического соотношения:

АсоАх > 2я.

Отсюда при Ат 00 и, естественно, Аю —> О возникает условие гармоничности. В этом случае все частоты ансамбля гармонически связаны и, более того, вырождены. То есть имеет место «перекачка» энергии с высших уровней на нулевой, частотой которого и определяется время жизни. На самом деле физический смысл состоит в том, что колебания высших частот, взаимодействуя, создают картину деструктивной интерференции. Понятно, что одними энергетическими принципами при анализе ансамбля не обойтись и необходимо привлечение волновых представлений.

Вообразить существование вечных ансамблей достаточно трудно, тем не менее ю этого условия применительно к высшим резонансам ансамбля вытекает, что электроны в ансамбле из нескольких сортов атомов будут колебаться так, что конфигурация их взаимного распо- ложеьшя вокруг ближайшего ядра будет соответствовать конфигурации в атоме благородного газа. Отсюда, в частности, вытекают свойства электроположительности и электроотрицательности, а также правило валентностей.

При рассмотрении ансамбля частиц как резонансной системы становится ясно, что энергия связи или, другими словами, дефисг энергии или массы, обусловлена деструктивной интерференцией колебаний, а само взаимодействие в ансамбле имеет прозрачный оптический смысл, заключающийся в образовании устойчивых интерференционных систем или динамических голограмм. Отсюда понятно, что инструментальные наблюдения микроструктуры вещества не просто напоминают интерференционные картины, а ими, собственно, и являются.

Беглый анализ собственных атомных частот известных химических элементов показывает, что абсолютно совпадающих среди них нет, и возникает естественный вопрос: каким образом в этом случае могут вообще об-

разеваться устойчивые системы? То есть необходимо обсудить механизмы частотной гармонизации, обеспечивающие образование химических соединений и вообще конденсированных сред.

Собственные резонансы плазмоподобной среды всегда модулированы. Во-первых, это интермодуляция, о которой говорилось выше, то есть влияние на один резонанс всех других. Это собственные, внутренние причины уширения полосы частот, занимаемой резонансом. Во-вторых, всегда существуют внешние поля, проявляющиеся в радиационном, гравитационном обмене и изменении термодинамических характеристик. Это является другой причиной уширения резонансных полос, благодаря чему возникают условия для их перекрывания, а соответственно, и для образования связного ансамбля. На этом обстоятельстве основаны практически все материаловедческие технологии.

Наиболее известным технологическим приемом получения некоторого вещества из исходной смеси других является использование тепловых приемов обработки. Обычно при достижении некоторой температуры возникают реакционные условия, и образуется новое вещество. При охлаждении свойства его, конечно же, меняются, но, тем не менее, по сравнению с исходными компонентами это нечто иное. Каким образом в этом случае достигается согласование (гармонизация) частот, можно понять, вспомнив поведение ансамбля разночастотных осцилляторов под действием вынуждающей силы. Все они через некоторое время начинают осциллировать с частотой вынуждающей сршы. Для ансамбля частиц такой частотой становится низшая частота самого ансамбля. Это явление, естественное для теории колебаний, известно и как принцип макрокинетики, утверждающий, что система высшего уровня стабилизирует системы, ее образующие. Более детально механизмы образования нового материала можно проанализировать с помощью дисперсионных уровней для волн в среде и во внешних полях.

Линейные размеры объемных плазмонов, по сути являюпщхся структурозадающими полями в среде, непосредственно определяются условрмми образования стоячих волн соответствующих резонансных частот. Можно также связать эти размерные параметры с радиусом дебаевского экранирования. Как известно,

D = Гр = 1 / (4ле2п / (кТ))”2 и

сОр = (4яе^п /

Отсюда, так как Я, = c/v и при с = 1 Гр = Я X (кТ / mY^I (2я).

То есть по-прежнему мы имеем дело с длиной стоячих волн, определенных с поправкой на температуру среды. Возможно и более точное определение размеров с учетом иных возмущений среды и динамического характера дебаевского экранирования, поскольку вышеприведенная формула учитывает только кулоновское взаимодействие. То, что мы имеем дело с плазмонами, размеры которых определяются длиной стоячих волн, можно пояснить и из следующих соображений. Структура поля из стоячих волн, декорируемая вещественными структурами, задается полями, напряженность которых зависит от расстояния как функция г\ подобно полю обычной антенны в дальней зоне. В то же время в плазмоне, как в ближней зоне антенны, реализуются поля, зависящие от г”^ и г’^, которые сами по себе без каких-либо граничных условий образуют стоячие волны с теми же самыми характерными длинами.

Как следует из таблицы 4.2, плазмоны, обусловленные внутриатомным ядерным резонансом, контролируют структуру самого атома или его ближайшего окружения с размерами порядка атомного радиуса. Плазмоны с частотами электронного резонанса в атоме определяют структуру, не имеющую прямого отношения к молекулярному устройству среды, с размерами порядка 30 нм. Это заведомо надатомное строение вещества. Причем если ядерный резонанс, а соответственно, атомно-молекулярный ближний (химический) порядок существенно зависит от конфигурации ближайшего электронного окружения, с вариацией частот в широчайшем диапазоне (0-^10’* Гц), то электронные резонансы сосредоточены в довольно узкой полосе частот порядка Гц практически в лю

бой среде. То есть регулярные электронные плазмоны среды в принципе могут отличаться своей внутренней структурой самым решительным образом. Можно даже утверждать, что соседние плазмоны могут состоять из совершенно разного вещества.

Электронные плазмоны с размерами около 30 нм и более крупные структурные образования типичны для абсолютного большинства сред. Их индивидуальность определяется в основном высшими резонансами, то есть плазмонами с размерами порядка атомных. Как уже говорилось выше, образование плазмонов связано с интерференцией электронных волн на частотах резонансов. Физическая картина упорядочения структуры вещества состоит в том, что заряженные частицы в электромагнитном поле могут как получать энергию от поля, так и отдавать ему. При этом если частоты колебаний частиц какого-то сорта выше суммарной (средней, грубо говоря) резонансной частоты, то такие частицы возбуждают поперечное электромагнитное поле, свободно покидающее среду. Поперечное электромагнитное поле с частотами ниже резонансной, возбуждаемое другим сортом частиц, не может покинуть среду, и его энергия расходуется на раскачку продольных резонансных колебаний, то есть плазмонов. В результате частота обоих сортов частиц подтягивается к общей резонансной частоте, образуя гармоничный ансамбль. Изменение внутриядерных атомных частот соответствует изменению и условий резонанса электронов и ядра. Часть электронов в результате этого как бы может быть отдана либо, наоборот, присовокуплена ионами. Устанавливается некоторый ближний порядок в пределах электронного плазмона. Этот порядок характерен тем, что индивидуальность ионов для него безразлична и они, в принципе, свободны в выборе своего места в пределах области конструктивной интерференции, то есть своего плазмона. Это связано с тем, что последний ограничен поверхностью постоянного потенциала и ион может перемещаться по ней без затрат энергии. В результате ионы распределяются в объеме плазмона под действием кулоновских или иных взаимодействий, формируя его структуру.

Предположим, однако, что среди ионов есть небольшое количество примесных, у которых отличается заряд, а соответственно, и масса ядра. Это обстоятельство может быть безразличным для высокочастотных плазмонов, поскольку в результате «обмена электронами» ион стал подобен благородному симметричному атому.

В котором отсутствует ядерный резонанс. Но для низкочастотных резонансов это ядро (и ион) по-прежнему существует. Причем примесь, обладая собственной резонансной частотой и «свободой выбора» места в высокочастотных плазмонах, занимает в них место в соответствии со структурой собственного низкочастотного плазмона, участвуя в присущем ему движении. Увеличивая концентрации примеси, можно уменьшить амплитуду движения ее ионов до размеров регулярного электронного плазмона (~ 30 нм) и локализовать примесь в нем. При температуре, близкой к абсолютному нулю, Е = hv , и поскольку Е = шА^со^/ 2, так как

то

п = (AVmn^Z^).

Отсюда предел «свободного» вхождения примесей, не локализованных в электронных плазмонах, то есть при А ~ 30 нм. Напрршер, для наиболее легкой частицы — протона

п ~ 10^^ м’^ – 10’’ см‘^

при частотах ее возбуждения около 6,6 х 10’° Гц. То есть число «естественно-растворенных» частиц соответствует примерно числу регулярных электронных плазмонов, убывая по мере )©еличения ионной массы примеси. Фактически примесь сосредоточена в интерплазмонном пространстве, образованном деструктивной интерференцией электронных колебаний среды. Для вхождения ее вовнутрь электронных плазмонов существует и естественный энергетический барьер, связанный с тем, что частоты объемных плазмонов выше в 2”^ раза частот поверхностных стоячих волн. Это известное из элект- родинамрпси обстоятельство для микроплазмонов представляется совершенно естественным. Действительно, для частицы, движущейся в объемном плазмоне по круговой орбите, энергия соответствует сумме энергий двух нулевых нормальных колебаний, в то время как линейные колебания в узловом пространстве — только одного. Отсюда Eq= 2Е^, и для частиц одинаковой массы при равных амплитудах, определяемых полуволновым пространством из Е = гпА^со^ / 2 получаем

= 2со ^

со =со./2”^

Следовательно, чтобы примесь стала ассоциированной электронным плазмоном, необходимо, чтобы ее частицы имели удвоенную за счет ортогонализации колебаний энергию. Это возможно за счет внешних воздействий, например, с помощью сторонних электромагнитных полей либо при охлаждении исходной смеси, концентрация примеси в которой более чем в два раза выше определяемой. Отсюда же можно определить и величину необходимой энергии:

Е ~ hV (2я^т),

которая оказывается достаточно малой и, например, в электронном процессе обеспечивается потенциалом порядка 10 ’ В или за счет теплового движения при температурах уже вблизи абсолютного нуля. Отсюда следует, что примесные ионы практически всегда ассоциированы электронными плазмонами и являются участниками высших атомных резонансов.

Поскольку концентрация ионов в среде определяется электронной плотностью и, как показано выше, имеет порядок 10’’^ 10’^ ионов в кубическом сантиметре, то рост концентрации примеси сопровождается снижением концентрации матричных ионов. Возникает вопрос: до каких пределов может происходить замещение основных участников высших резонансов? Здесь первостепенное значение имеют колебания ионов как целого. Дело в том, что самосогласованный ансамбль основного вещества представляет собой систему из ионов, колебания которых синфазны и антифазны. Тем самым и достигается упорядоченная интерференционная структура среды. При небольших концентрациях примесных ионов их резонансное продольное электромагнитное поле лишь слегка модулирует поле среды низкочастотными колебаниями. Но по мере увеличения концентрации примеси ее парциальная частота растет, в то время как частота среды снижается вследствие уменьшения концентрации ее собственных ионов. Эти изменения сопровождаются, естественно, изменением структурных параметров. То есть в отношении кристаллов, например, должно наблюдаться изменение параметров решетки, обусловленное изменением частоты, а соответственно, и амплитуд колебаний частиц. Присутствие примеси подобно наличию ионного газа, давление которого «распирает» среду либо, напротив, компенсирует некоторый «вакуум», являющийся следствием рассинхронизации электронной и ядерной плотности среды за счет индивидуальных особенностей атомного строения. Напомним, что мы имеем дело с тремя резонансными частотами, зависящими от концентрации электронов, заряда, массы и концентрации ядер ионов, и частотой внутриионного колебания ядра. Для образования устойчивой системы эти частоты должны удовлетворять гармоническим условрмм. В тех случаях.

когда одна из частот «выпадает», присутствие примеси является необходимым условием стабилизации.

При сближении ядерных частот «матрицы» и примеси, с возрастанием концентрации последней, их разностные частоты проходят ряд кратных отношений. То есть фактически ряд

пр’’

где к — целые числа. Каждое такое состояние соответствует образованию регулярной примесной структуры, гармонически сопряженной со структурой матрицы, то есть, говоря обычным для химии языком, ионы примеси замещают ионы матрицы. Это явление имеет собственное имя — изоморфное замещение. Существует, в принципе, ряд изоморфных концентраций примеси, который можно определить из условия:

ИЛИ подставляя выражение для плазменных частот: п /т. = п kVm

п = п (Z /Z )^т. / (т. к^)

Из последнего выражения видно, что при малых к оно эквивалентно условию для взаимодействующих ионов и мало чем отличается от химического родства. Родство изоморфизма к химическому соединению проявляется и при больших кратностях. Но с увеличением кратности сокращается время жизни изоморфного состояния, поскольку с ростом Av, Ат—>0, так как AvAt ~ 1. Отсюда следует также, что процессы структурирования в любой замкнутой системе из частиц, начавшись из хаоса, проходят через пик гармонизма (совершенства, когда все частицы играют свою роль в ансамбле), заканчиваются при достаточном времени эволюции полной сегрегацией на электронные плазмоны, внутри которых высшие

резонансы образованы ионами одинаковых зарядов и массы. Физическая картина сегрегации состоит в том, что при наличии гармонических отношений в ансамбле он может быть представлен и как совокупность стоячих волн. Это относится и к резонансному магнитному полю, и к распределению мгновенных амплитуд колебаний частиц. Наличие уже двух стоячих волн определяет появление бегущей низкоскоростной волны, которая изменяет фазовые соотношения колеблющихся частиц. Теперь они являются ни синфазными, ни антифазны- ми. В результате возникает дрейф частиц одного сорта по отношению к среднему положению частиц другого сорта, заканчивающийся их разделением на самостоятельные вещественные фазы.

Сказанное выше относится не только к замкнутым системам. При наличии каких-либо процессов обмена со средой скорость эволюции возрастает. Например, при возможности электромагнитного обмена колебания с частотами выше резонансных быстро затухают за счет излучения, вместо длительного процесса релаксации внутри замкнутой системы. При недостатке энергии для раскачки плазмонов она может быть получена за счет поглощения. Естественно, что пути эволюции структур при этом совершенно различны.

Дрейф частиц в ансамбле не является монотонным, за исключением, может быть, дрейфа протонов. Дело в том, что ион помимо ядра имеет и «электронную оболочку». Электроны адиабатически следуют за ядром, пока частоты колебаний последнего меньше характерных электронных частот, то есть являются результатом парциальных ядерных резонансов. Но электроны в ансамбле образуют устойчивую интерференционную структуру, ядра в которой расположены подобно ядрам благородных газов. Смещение ядер под действием внутренних или внешних сил вызывает появление упругой силы и возбуждение колебаний на частотах выше парциальных. Рассогласование этих частот вызывает перестройку электронного окружения, подстраивающегося под колебания ядра, то есть сопровождается возникновением новых резонансов. При появлении частот, кратных основным, поляризация ионов достигает таких значений, при которых становится возможен обмен ионов местами при антифазных амплитудах их ядер. Можно показать, что величины энергий, необходимых для этого, весьма малы, и выше говорилось уже о том, что движение большинства примесей по ансамблю практически не требует активации и реализуется в природных и технических процессах. Конечно, это верно лишь, если примесь моноионна и не образована самостоятельным плазмоном. Последний (например, молекулярный ион) имеет более широкий спектр резонансов, удовлетворить которому для смещения иона как целого гораздо сложнее. Субгармонические резонансы, соответствующие «перевернутому» выражению = nv^, на самом деле являются результатом «растворения» не примеси в матрице, а скорее наоборот, матрицы в примеси. Дело в том, что электромагнитные волны с частотами меньше резонансных в матричных плазмонах «интенсивно» поглощаются и распространяться не могут. Плазмоны матрицы в низкочастотном поле колеблются как целое, но только при значительно меньших частотах, чем частоты собственно матричных резонансов.

Для легких ионов частоты электронных и парциальных ядерных резонансов, как определено выше, отличаются более чем на порядок. Но с увеличением массы иона растет и заряд его ядра. Причем в выражении для частоты парциального резонанса со ~ eZ (п / т)”^ влияние роста заряда более существенно, чем увеличение массы. Следовательно, с увеличением массы ионов происходит сближение частот электронных резонансов, зависящих в основном от внешних электронов и потому слабо меняющихся, с парциальными ядерными резонансами. В то же время ионные резонансы, обусловленные колебаниями ионов как целого, с увеличением массы испытывают уменьшение частоты, поскольку заряд иона определяется, опять же, только внешними электронами. Рост массы иона на два порядка по сравнению с массой водорода приводит к уменьшению частоты ионного резонанса примерно на порядок, с одновременным увеличением парциальной ядерной частоты в несколько раз. При этом частоты электронного и парциального ядерного резонанса могут оказаться и равными. Однако уже при их сближении, в результате возникновения биений и соответствующих бегущих волн, среда приобретает довольно необычные свойства, выражающиеся в подвижности ее фрагментов, то есть пластичности. «Вырождение» резонансов в результате внешних воздействий, например, вариаций температуры среды, сопровождается увеличением пластичности либо переходом в жидкое состояние не только для тяжелых ионов. Однако «тяжелые» среды интересны еще и тем, что могут «растворять» в себе «легкие» примеси в таких количествах, когда концентрация последних во много раз выше концентрации их в свободном состоянии. Это обусловлено тем, что примесь является таковой до тех пор, пока ее парциальная резонансная частота не сравняется с частотой матрицы. При превышении частоты примесь образует собственную фазу. Поэтому в среде из «тяжелых» ионов, где парциальные ядер- ные частоты высоки, концентрации легких примесных ионов могут достигать величин, в десятки и более раз превышающих концентрацию ионов матрицы: п = п m / (Z^ m ), где Z — заряд ядра; m — масса иона.

Причем примесь и вообще ионный матрикс в «жесткой» электронной структуре очень подвижны. Следует подчеркнуть еще раз, что дрейф частиц в ансамбле и эволюция его структуры, в принципе, имеют место всегда и не требуют внешнего воздействия, но последнее может существенным образом изменить как скорость, так и направление эволюции. Низкоактивационные процессы составляют основу природного метаморфизма и ныне широко используются в технологии.

Детальное рассмотрение движения частиц необходимо проводить с учетом полной, то есть лоренцевской, силы. Причем во многих случаях ее динамическая составляющая, зависящая от скоростей и напряженностей магнитного поля, может оказаться более значительной по сравнению с кулоновским взаимодействием, не только для внутриядерных взаимодействий, как отмечалось выше, но и на уровне атомных и надатомных структур. Однако для низкочастотных полей часто можно ограничиться учетом только электрических взаимодействий, хотя ориентационное воздействие магнитного следует иметь в виду.

Крайний случай низкочастотного поля — постоянное электрическое — для плазмоподобной среды про

является в ее поляризации, обусловленной нарушением симметрии плазмонов. Действительно, силы, действующие на заряды противоположного знака, являются причиной возникновения нового типа колебаний, частота которых может быть определена из рассмотренных выше моделей, приводящих к известному выражению для энергии колебаний:

Аф = hv,

где Аф — разность потенциалов стороннего поля на противоположных границах объемного плазмона. При неопределенных соотношениях частот, возникших под действием стороннего поля, и собственных плазменных частот поляризация среды определяется только этим полем. Однако при рациональных отношениях:

где к — целое число, индуцированное поле в сочетании с собственным резонансным полем плазмонов порождают медленные бегущие волны, являющиеся суперпозицией стоячих. При этом, за счет дрейфа зарядов, меняются их распределение в плазмоне, его конфигурация и характер интегральной поляризации. Поэтому поляризуемость среды, а соответственно, и диэлектрическая проницаемость ее не являются монотонными функциями напряженности поля, но зависят от гармонических составляющих собственных резонансных частот вещества. Направление медленных волн и дрейфа зарядов не обязательно совпадает с направлением их смещения под действием поля, поскольку зависит от знака расстройки синхронизма колебаний.

Следует также учитывать, что электромагнитное поле, возникающее в среде под действием постоянного электрического поля сторонней природы, существенно лишь при частотах, соответствующих собственному резонансу в плазмонах. Это является следствием того, что на более низких частотах среда непрозрачна и во взаимодействии участвуют лишь поверхностные слои вещества с толщиной порядка длины волны индуцированного поля. При больших значениях к, а соответственно, при низких напряженностях поля, глубина поляризации не так уж и мала и для электронных плазмонов достигает долей миллиметра. В спектре диэлектрической проницаемости существенно, вероятно, и участие поверхностных плазмонов с частотами меньшими частот объемных в 2’^^ раза.

Напряженность стороннего поля, возбуждающего колебания с частотами, близкими к резонансным частотам среды, может быть определена как

Е » Дф / Аг,

где Ат — характерный размер плазмона. Так как Аф = hv и Аг » с / V , то

E«hv 2/с,

а для резонансов на «субгармонических» частотах E*hvJ/(nc), здесь п — целые числа.

Возбуждение плазмонов, обусловленных парциальными колебаниями ядер ионов среды, с характерными частотами Гц требует поля с напряженностью

порядка 10^^10^ В/м. То есть уже при такой, достаточно низкой, напряженности вещество приобретает существенно нелинейные свойства. Поскольку частоты ядерных резонансов ниже частот электронных, то в большинстве случаев среда непрозрачна для поля, обусловленного колебаниями ядер, и их энергия расходуется на раскачку электронных плазмонов. Последнее про-

является в модуляции электронных частот, в спектре которых возникают новые компоненты v = ± v^. Это

явление соответствует известному штарковскому расщеплению. Причем в среде частоты v = «реаб-

сорбируются», а компоненты v = + v^, будучи выше

резонанса v^, могут «излучаться» во внешнее пространство. Подбором матричного вещества и изоморфных ионов, образующих надатомные плазмоны с частотами в «окнах прозрачности» матрицы, можно реализовать генераторы радиочастотного диапазона.

При напряженностях стороннего поля 10’-^ 10^ В/м возбуждаются электронные резонансы с частотами Гц. Совокупность трех волн, связанных с частотами колебаний под действием стороннего поля и частотами собственных резонансов среды, при близости двух высших частот соответствует известной системе, склонной к самовозбуждению. При этом амплитуды колебаний зарядов экспоненциально нарастают, и плаз- монная структура разрушается. Перенос зарядов определяется теперь преимущественно силами стороннего поля. Ситуация, очевидно, соответствует электрическому пробою диэлектрика.

Можно показать, что все ионно-молекулярные и атомные особенности индивидуальных элементов и соединений имеют резонансный характер и могут быть описаны непосредственно на языке теории колебаний в рамках голографической модели вещества. Последняя, напомним, исходит из того, что системы любой сложности есть суперпозиции электромагнитных полей, связанных в гармонический волновой пакет и обладающих отличным от нуля ротором механического импульса. Подробное описание не входит в задачи данной работы.

целью которой является анализ кооперативных процес- сов в средах, обладающих достаточно общим характером. Выше показано, что в электромагнитном спектре любой среды, состоящей из заряженных частиц, или на языке модели из электромагнитных полей с замкнзо’ым вектором Пойнтинга (rot Р ф 0), присутствует несколько фундаментальных полос, обусловленных резонансами в ядре, в электронном «газе» и в парциальных колебаниях ядер. Кроме того, в спектре может наблюдаться большая совокупность комбинационных полос и полос, обусловленных наличием примесей. Достаточно очевидно, что воздействие электромагнитного поля с частотами, близкими к резонансным, в отличие от постоянного электрического поля, имеет прямой характер и изучено, быть может, лучше многих других. Некоторые детали таких процессов рассмотрены выше.

Отдельного внимания требует поведение плазмоподобных сред в механических и термомеханических полях, поскольку общность этих процессов с рассмотренными выше не вполне очевидна.

установившихся колебаний для резонансных частот

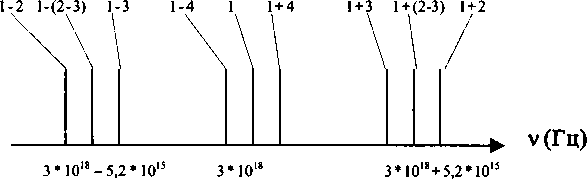
Рис. 4.1.2. Спектр коротковолновой компоненты резонансного поля

2-3 2-4 2 2+4 2+3

\/ \

1 !-► V (Гц)

(5.2-1,6) *10’’ 5,2»10‘^ (5,2+1.6) *10”

1Я) = (4яе2п/(кТ))>’2.

<0 = Юь,

1 к’

111 к к к

111 к к к

^0)y = co^9iO,

i

© = (e^Z^n / (8дП1))‘’^,

О п

ИЛИ

п О

V = kv

V 2 = k^V 2

м пр

М М 1М пр пр 1Пр

пр М М пр^ 1ПР 1М ^

V = kv,

т пл пл’

пл ’

КОГЕРЕНТНОСТЬ

В оптике и технике высоких частот при описании электромагнитных полей широко используется понятие их когерентности как меры пространственной и временной согласованности или упорядоченности отдельных составляющих. Это понятие имеет непосредственное отношение и к анализу структуры вещества, поскольку его голографическая модель ничего, кроме электромагнитного поля, не рассматривает. Что касается пространственной, то есть структурной, когерентности, то можно немедленно выделить труппу кристаллических сред как наиболее устойчивых. Кристаллы, как правило, имеют и высокую временную когерентность.

Интуитивно ясно, что некоторой степенью когерентности обладают не только твердофазные среды, но и жидкости и газы, в отношении которых признается лишь ближний порядок. Наибольшей же степенью неопределенности, в современных научных представлениях, можно охарактеризовать структуру аморфных сред, к числу которых относят и один из важнейших материалов — стекло. Понятие «когерентность» в рассматриваемой модели позволяет выработать достаточно общий подход к определению порядка в конденсированных средах и наметить схему классификации реальных структур.

В оптических экспериментах основная роль отво- дрггся электрической напряженности поля ввиду того, что магнитная практически не меняет энергию зарядов вещества. В связи с этим обычно исследуется только согласование электрических компонент поля. И уже совсем не берется в расчет механическая компонента:

Выше мы обращали внимание на то, что модели, учитывающие только кулоновское взаимодействие, корректны далеко не всегда. Например, неучет динамической компоненты взаимодействия приводит к расхождению с реальной плотностью ядра на 2-3 порядка. Причем известно, что вклад кулоновского взаимодействия в энергию ядра составляет именно величину порядка одного процента. Это подтверждает хорошее соответствие плазменной модели реальному положению дела, при надлежащем выборе вида возвращающей силы. Основная трудность использованР1я полной силы

Лоренца состоит в том, что ее динамическая компонента является неосевой, в отличие от кулоновской. При очень низких концентрациях частиц ее можно учитывать, например, в форме дипольного приближения либо попросту не включая в рассмотрение. Однако при высоких плотностях (ядро) или высоких напряженностях магнитного поля частиц (металлы) ее роль начинает доминировать, причем в условиях, когда размеры «траектории» частицы соотносимы с межчастичным расстоянием. Такое взаимодействие существенно отличается от кулоновского тем, что всегда реализуется только притяжение, которому предшествует ориентация элементарных голограмм, контуру которых соответствуют траектории классических частиц. Траектории частиц в плазмоподобной среде есть не что иное, как сама частица, точнее, ее голограмма. Кольцевой контур, соответствующий вихревой линии импульса, — это контур с элементарным током. Два таких контура, предоставленных самим себе, проворачиваются таким образом, что оси их совпадают и контуры занимают положение устойчивого равновесия. А так как «токи» в них имеют после этого одинаковое направление, то они начинают притягиваться, существенно компенсируя кулоновское отталкивание. В результате этого становится возможным образование устойчивых структур ядер атомов из протонно-нейтронных пар. Заметим, не отвлекаясь далеко от темы работы, что образование ядер только из протонов невозможно, поскольку кулоновское отталкивание несколько больше магнитного притяжения. Подобно магнитному взаимодействию элементарных голограмм осуществляется и их механическое, которое во многих случаях есть прямое следствие первого. Однако

если магнитный момент голограмм «экранирован», то механический приобретает самостоятельное значение. Они так же, как и магнитные, ориентируются вдоль одной оси, после чего голограммы начинают испытывать «притяжение». Употребляя термин «голограммы», мы подчеркиваем безразличное отношение к уровню и масштабу взаимодействующих указанным образом систем. Это могут быть, например, звезды и планеты, то есть механическое взаимодействие включает в себя и гравитационные явления. Но не наоборот, ибо под гравитацией принято подразумевать только притяжение тел, оставляя в стороне ориентационные эффекты. Таким образом, в соответствии с тремя видами напряженностей электромагнитного поля можно выделить и три рода взаимодействий поля с веществом, а соответственно, и в самом веществе: электрическое, магнитное и механическое. Оставив без рассмотрения их крайние по интенсивности проявления, такие как ядерные и гравитационные, обратимся к анализу надатомных струюур. Каждому роду взаимодействий соответствует некоторая голограмма, «выполняющая» этот процесс. Например, атомы объединяются в новую голограмму (молекулу), обобщая электроны или перераспределяя их между собой. Частица, ответственная за это взаимодействие, — электрон. Существует класс соединений обменного типа, взаимодействие в которых имеет магнитную природу со своим носителем — магноном. Эту частицу считают обычно квазиобъектом. Другая квазичастица — фонон — ответственна за относительно слабые механические взаимодействия в конденсированных и газообразных средах. Однако с этим трудно согласиться, так как механическое воздействие на ма

териалы, реализующееся в рождении фононов, нередко столь сильно, что приводит к разрушению либо пластической деформации.

Проблемы структуры вещества в последние сто с небольшим лет свелись, в значительной мере, к чисто геометрическим задачам: плотных упаковок, симметрий и т. п. Квинтэссенцией геометрического подхода является удачное описание реальных структур с помощью представлений пространств с кривизной. В то же время под термином «структура» издревле подразумевалось не только пространственно-упорядоченное расположение каких-либо элементов, но и характер связей между ними. Более того, этимология слова «структура» восходит к глаголу «строить» (строительство), то есть соединять два элемента третьим. Однако по вполне объективным причинам дифференциация в исследованиях достигла необычайной глубины и связи между элементами структуры изучаются вне связи с самой структурой.

Развиваемые в этой работе представления возвращают к изначально комплексному пониманию структуры вещества. Естественной для голографической модели является «оптическая» терминология, в которой порядок обозначается понятием «согласованность», то есть «когерентность». Последняя определяется характером взаимодействий, и поэтому следует, видимо, выделить три ее типа: электронную, магнонную и фононную. Совершенно ясно, что в чистом виде трудно выделить примеры вещества, где реализуется лишь один из трех типов когерентности. В то же время ионные кристаллы очень близко соответствуют представлению об электронном характере связей и порядка, ими обусловленного. С другой стороны, магнонные связи между ионами должны «освободить» от этой функции электроны. Что и наблюдается у металлов, где электроны проводимости обеспечивают не связи, а только электронейтральность. Наконец, существует и третий класс материалов, который трудно отнести к электронному или магнонному типу. Это стекла, для которых среди «упорядоченных» веществ места пока не определили, отнеся их к аморфным. На взгляд автора, эта проблема существует как пробел в исследовательских экспериментальных методах. Дело в том, что существующие методы исследования ориентированы на регистрацию структурных фрагментов, обладающих электрическим зарядом. Таковыми являются дифрактометрия в рентгеновских лучах и другие отработанные методы. В то же время фононные структуры могут демонстрировать (и на самом деле так и происходит) полную электрическую индифферентность структуры. Вполне возможно, что структуры фононного типа можно изучать с помощью дифракции ультразвука достаточно высокой частоты. Но отсутствие четких дифракционных рентгеновских рефлексов и ультразвуковых дифрактометров — вероятно, не все проблемы. Традиционные представления о правильности структуры основываются на евклидовой геометрии и, более того, в качестве эталона используют плоскость. Все кристаллографические группы описывают, так или иначе, семейства точек, образующихся при пересечении плоскостей. В голографической модели структура — это интерференционная картина, которая вовсе не обязательно представлена набором прямых линий, плоскостей и «точек» их пересечения. Скорее наоборот, «евклидовы» наборы — всего лишь частный случай. Возьмем, например, плоскую фигуру

Лиссажу, которая есть результат интерференции двух волн с большим отношением частот (рис. 4.2.1).

В центре интерференционной картинки можно увидеть почти правильную классическую решетку. На самом деле ясно, что «правильная» решетка — явление каж)оцееся, а реальность состоит в том, что она образована линиями высших порядков и даже трансцендентными кривыми типа тригонометрических. Полное описание порядка в представленном примере из наблюдаемого материала, вероятно, крайне проблематично. Но если дифрактометры «научатся» регистрировать хотя бы поверхности высших порядков, то традиционная классификацрм структурных мотивов усложнится невероятно. Вернемся к типам когерентности вещества с целью проанализировать возможность существования промежуточных, вернее, комплексных, классов материалов. Например, если наряду с электронными связями будут иметь место магнонные, то в результате получится ни диэлектрик, ни проводник с хорошо выраженной кристаллической структурой. Такой класс материалов хорошо известен — это полупроводники. Далее, хорошо известен также и класс материалов, обладающий свойствами полустекла-полукристалла, — стеклокри

сталлические образования, относящиеся к электронно-фононному типу когерентности. В последние десятилетия широко исследуются свойства материалов с магнонно-фононным типом когерентности — металлические стекла. И, наконец, нельзя обойти вниманием возможность одновременного наличия всех трех типов связей, вероятно, представляющую наиболее широкий класс материалов на уровне индивидов, включая, например, биологические и минеральные. Подведем итоги анализа в таблице типов когерентности и классов соответствующих материалов.

Тип когерентности

Класс материалов

1

электронная (Э)

ионные соединения

2

магнонная (М)

металлы

3

фононная(Ф)

стекла

4

эм

полупроводники

5

ЭФ

стеклокристаллические

6

МФ

металлические стекла

7

ЭМФ

живые

Итак, по характеру связей могут существовать семь типов когерентности вещества, из которых шести можно сопоставить известные классы материалов.

СТРУКТУРЫ

Сложилось так, что вопросы организации надатом- ных струетур в современном материаловедении остались изучены в совершенно незначительной степени в сравнении с устройством вещества на микроуровне. Ионно-молекулярные механизмы и электронные плотности, конечно же, являются важнейшим уровнем в познании природы вещества и конструировании эффективных материалов. Тем не менее важность нада- томной организации известна давно, и исследованию ее свойств посвящено множество работ в совершенно различных областях материаловедения, начиная с металлургии и заканчивая технологией широчайшего класса силикатных материалов. И хотя в практической технологии получено множество рецептов организации надатомных структур, в теоретическом плане наблюдаются лишь незначительные подвижки.

Долгое время исследование в этой области ориентировалось на изучение минеральных фаз, а там, где минералогия и петрография не могли выделить «свои» объекты, вступали туманные представления о доменах, кластерах, мицеллах и т. п. Следует отметить, что именно минералогическое и петрографическое исследование в этой области было наиболее продуктивным. Однако, в отличие от атомного уровня, где существует богатейшая теоретическая база квантовых механики и химии, надатомная организация вещества теоретическими подходами не избалована. Лишь в последние десятилетия появилось, например, такое направление, как мезомеханика, пытающееся на известных квантовых принципах «расшифровать» природу дислокаций и других «дефектов» твердого тела. Существует и ряд иных попыток использования новых представлений, например, теории фракталов. Очень может быть продуктивен подход, использующий неевклидовы представления пространства, позволяющий включить в точечные многообразия «элементарные» структурные «кирпичики» — прима-тела Чепижного и интегрирующее их на следующем иерархическом уровне «критиче- ское тело» Руднева.

На примере плазмоподобной модели выше уже рассмотрены некоторые иерархические соподчиненные размерно-структурные уровни надатомной организации ветцества. Здесь же подчеркнем важность понятия когерентности. Основное голографическое соотношение

имеет непосредственное отношение к оптическому определению когерентности. В приведенной форме оно отражает временной аспект согласования осцилляторов. Например, для ансамбля с набором частот, характеризуемым разностью высшей и низшей Av, время жизни определяется в виде Ах = 1 / Av. То есть чем шире (некогерентный) частотный спектр ансамбля, тем короче время его жизни. Это имеет непосредственное отношение и к веществу: чем уже набор минеральных фаз в породе, например, тем она более долговечна. По- лиминеральные породы, в свою очередь, разрушаются быстрее. Или, на другом уровне, чем меньше в минерале изоморфных примесей, тем он более долговечен. В этом случае можно говорить о ширине спектра изоморфных замещений. Соотношение неопределенностей, имеющее смысл временной характеристики импульса или ансамбля, может быть преобразовано в отношении пространственной характеристики импульса (в нашем случае ансамбля) к виду:

АкАг> 1,

Ак — ширина полосы волновых чисел, k=1/>. = v/c; X — длина волны; с — скорость света;

Аг — размер ансамбля.

Отсюда следует, что размеры пространственно-когерентной области вблизи базовой голограммы (частицы) обратно пропорциональны ее характерной частоте или пропорциональны соответствующей длине волны. Действительно,

Дк = – к, = 1 / – 1 / A.J

и

а так как, как правило, A,j, то Аг < А,,. Отсюда, поскольку для протона (таблица 4.2) X. ~ 1 то и размер когерентной области Дг ~ 1 X» что соответствует диаметру атома водорода. Характерные частоты в атоме ~ Гц имеют А, ~ 30 нм и, следовательно, кон

тролируют новую голограмму с тем же размером порядка 30 нм. Две другие характерные частоты из таблицы 4.2 контролируют голограммы с размерами порядка 0,1 мкм и 1 мкм. Наличие структур указанных размерных порядков является свидетельством когерентности материала и, получается, является достаточно общим свойством всех конденсированных сред. Можно провести некоторую аналогию между элементами последних указанных групп (0,1 мкм и 1 мкм), с одной стороны, с «прима-телами» Чепижного и «критическим телом» Руднева — с другой. Элементы структуры с размерами порядка 30 нм являются, вероятно, важнейшим надатом- ным уровнем организации вещества, поскольку электроны, обеспечивающие их существование, находятся в когерентном движении. Вследствие этого суммарный момент количества движения, дипольный и магнитный моменты существенно не нулевые и надатомный элемент структуры ведет себя подобно частице. В равной мере это относится и к надатомным структурам с размерами 0,1 и 1 мкм. Обозначенные здесь размеры мезо- структурных элементов определены из простейшей модели, не учитывающей ионного многообразия. И хотя это достаточно типичные размеры, но в зависимости от конкретного набора ионов они могут сильно отличаться от указанных. Более того, существует, видимо, не только размерная, но и конфигзфативная дифференциация микроансамблей. К. И. Чепижный, например, выделял более двух тысяч структур из микроансамблей кубической, тетраэдрической и октаэдрической форм.

Ввиду того, что мезоструктурные элементы вещества обладают когерентностью с явно выраженными свойствами некоторого рода частиц (мезочастицы), то именно они ответственны за такие особенности вещества, как, например, доменные структуры сегнето- электрических и ферромагнитных материалов. Таким образом, надатомная организация вещества предстает в виде иерархизованных структур, последовательно возрастающих масштабов. Причем элементы структуры являются дискретными ансамблями частиц предыдущего уровня и сами обладают свойствами частиц.

При анализе когерентности вещественных структур возникает ощущение последовательного усложнения их: от наиболее элементарных (атомы) до все более крупных и развитых, типа кристаллических и иных образований. Действительно, иногда химизм на уровне ионной структуры задает последовательность дальнейшей эволюции вещества. Однако представляется необходимым учет не только детерминирующего влияния на эволюцию вещества его элементного состава, но и обратного влияния макроусловий и макроструктуры, то есть морфологических особенностей среды зарождения, на химизм и управление процессами развития мезоструктур.

Наиболее устоявшееся представление эволюции вещественных структур рассматривает их как результат последовательного упорядочивания единого массива среды на фронте некоторого фазового перехода. В пользу такого подхода свидетельствуют многочисленный экспериментальный материал по выращиванию монокристаллов и логика анализа. Действительно, если даже принять предлагаемую здесь резонансную модель процесса, то необходимо признать, что резонансные свойства определяются параметрами уже готового атомно-ионного материала среды. Но выше показано, что резонансы одновременно (то есть не последовательно) задают структуры в широчайшем диапазоне размеров от долей нанометра до микрометров. Более того, в проведенном выше анализе рассматривались резонансы на еще более низких частотах, но на самом деле они во многих случаях могут иметь определяющее значение в структурной эволюции.

Далее. Процессом, контролирующим рост монокристаллов, считается диффузия ионов через матричную среду на границе роста. Условия реального роста таковы, что вблизи фронта роста задается значительное переохлаждение матричной среды, благодаря чему возникают температурные градиенты, обуславливающие диффузию. С точки зрения резонансной (голографической) модели, температурные градиенты обуславливают «подтягивание» частот ансамблей среды к частотам растущего кристалла, то есть о «последовательном» процессе и здесь не приходится говорить, поскольку

образование мезоструюур происходит уже в самой ростовой среде.

Голографическая модель пригодна для рассмотрения любых уровней организации вещества с единой позиции. Далее при анализе динамики земной коры будет рассмотрен процесс развития высокочастотных структур вслед за образованием низкочастотных. Такая последовательность эволюции хорошо соответствует известному макрокинетическому принципу, согласно которому система высшего иерархического уровня стабилизирует продукты предшествующих. В противном случае необходимо привлечение некоторых дополнительных условий на образование системы высшего уровня, тогда как этого вообще не требуется при эволюции от целого к части. Наличие выделенного какими-либо границами объема вещества переводит его в разряд систем с вынужденными колебаниями, спектр которых определяется в первую очередь именно этими границами, то есть, по существу, заданной ими морфологией. В этом случае последняя предопределяет структурную эволюцию вещества, если спектр «внешнего морфологического» резонатора близок спектру собственных плазмоподобных резонансов.

Наиболее характерными примерами рассматриваемой морфоструктурной детерминации являются плодные объекты биологического царства в виде яиц, коконов, семян, яйцеклеток и даже материнской утробы. Структурное развитие плода контролируется морфологией его оболочки и происходит до тех пор, пока не сформируется его собственная поверхность, которая является важнейшим органом любого индивида. Дело в том, что дальнейшая эволюция определяется в значительной мере спектром поверхностных плазмонов. В этом отношении образование и развитие минеральных индивидов мало чем отличается от рождения биологических особей. Действительно, зарождение кристаллов и иных минеральных образований происходит, как правило, на границе раздела фаз под влиянием полей поверхностных плазмонов. Очень отчетливо это проявляется, например, в «правиле ортотропизма», согласно которому зарождение кристаллов происходит на границе, а растут они «внутрь» среды перпендикулярно поверхности. В этом случае зарождение новообразований индуцируется граничными полями, как и в другом — когда индукторами выступают частицы иной фазы, распределенной в веществе. Оба этих случая являют пример каталитического воздействия, характер которого может быть усилен Р1ЛИ ослаблен за счет подбора материала стенок или примесной микрофазы. Рассмотренный в общих чертах механизм каталитического управления эволюцией минеральных форм хорошо иллюстрируется процессами кристаллизации метасиликатов кальция и магния из стекол соответствующего состава. Например, стекла вол- ластонитового состава из переохлажденного состояния кристаллизуются в игольчатой Р-модификации, причем ориентация игольчатых агрегатов соответствует правилам ортотропизма, а фронт кристаллизации параллелен поверхности образца.

Скорость кристаллизации может быть увеличена во много раз присутствием на поверхности образца следов оксида трехвалентного хрома или, напротив, замедлена в присутствии окислов железа.

Другой пример каталитического зшравления реализуется при введении оксидов хрома в расплав стекла пирок- сенового состава. В этом случае нагрев переохлажденного стекла сопровождается образованием мелкозернистой структуры, индуцированной полем хромитов.

Морфоструктурный детерминизм легко понять с позиций голографической модели. Объемные и поверхностные плазмоны формируют в пространстве вещества стационарные полевые структуры, являющиеся аналогом фигур Лиссажу. Эти структуры характеризуются некоторым распределением электрических, магнитных и механических напряженностей, то есть, по сути, являются упорядоченной системой виртуальных частиц, с которыми взаимодействуют ионы и молекулы среды. Тем самым в структуре новообразования фиксируются исходные морфологические признаки. Здесь становится понятным и механизм реализации макроки- нетического принципа стабилизации системой вьющего уровня продуктов низщих. Действительно, наруще- ние исходной морфологии образцов при механической обработке, например, сопровождается существенной деградацией структуры, что требует высокого технологического искусства при обработке стекол, кристаллов и других материалов, чтобы избежать разрушения.

Параметры плазмонной структуры и спектр плазмоподобных резонансов существенным образом зависят от внещних термодинамических условий и электромагнитных воздействий. Откликом на изменение термодинамического состояния во многих случаях являются полиморфные переходы, сопровождающиеся изменением как структуры, так и облика минеральных индивидов или их фрагментов. Наиболее известны полиморфные состояния кварца. Для метасиликата кальция также характерны полиморфы а- Р- и у-. В ходе нашего экспериментального исследования структуры образцов волластонита, полученного кристаллизацией стекла, вьывлена еще одна модификация.

Фазовые переходы под воздействием электрических и магнитных полей также связаны с изменением параметров плазмонной структуры и соответствующей этому перестройкой доменной упорядоченности сегнето- электриков и магнетиков. Перестройка структуры под воздействием механических напряжений может быть сведена к рассмотренному ранее влиянию электрических и магнитных полей. Однако существует особый случай механического воздействия, представляющий общий интерес.

Выше отмечалось, что структура среды генетически наследует структуру стационарных плазмонов, обусловленную морфологией граничных поверхностей. Естественно при этом, что атомные и надатомные структуры среды играют столь же существенную роль, поскольку напряженности внешних полей компенсируются материалом того вещества, которое в данном случае есть. Поэтому в результирующих структурах фиксируются не только морфогенетические признаки, но и собственно структурные особенности среды, участвующей в зарождении и развитии индиврщуальной системы, например, минерального или биологического индиввда.

Несколько, может быть, неожиданное сравнение как нельзя лучше иллюстрирует органическое единство нашего мира, касающееся его глобальных и локальных аспектов. Б. Н. Родимов указывал на наличие резонансов в атоме водорода, обусловленных годовым обращением планеты вокруг Солнца. Действительно, Земля обращается не только вокруг

Солнца, но и вместе с ним по галактической орбите с линейной скоростью порядка 230 км/с. Скорость орбитального движения планеты в то же время — около 30 км/с. Поскольку полгода Земля движется «по Солнцу», а следующие полгода — «против Солнца», то ее скорость относительно галактических координат варьирует в течение года от 200 до 260 км/с.

◄ ^

Этого достаточно, чтобы в течение года вызвать катастрофические последствия, если бы вариации имели необратимый характер. К счастью, это не так, но не в силу каких-либо макроскопических механизмов, а за счет резонансов внутриатомных и кооперативных нада- томных структур. Полная годовая вариация кинетической энергии протона в атоме водорода составляет

Используя выражение для энергии АЕ = hAv, получим величину вариации в единицах частоты:

Av = АЕ / h = (2nipV V3) / h « 3,5 X 10‘” Гц.

Рис. 4.3.2. К суточной вариации кинетической энергии

Эта частота хорошо известна как электронная, и, следовательно, годовая вариация кинетической энергии протона соответствует элеюронному резонансу. Таким образом, электронные состояния водорода существенно отличны для периодов максимальной и минимальной годовой скорости планеты. Более того, удивительно совпадение вариации планетарно-галактического масштаба и электронного перехода в атоме. Сезонное различие электронных состояний водорода является прртчиной различий в его сезонной активности и, в принципе, хорошо известно в практической деятельности.

Но это, оказывается, не все. Дело в том, что соответствующая вариация электронной энергии в единицах частоты составляет величину порядка 10*^ Гц. Но, как показано выше, этот же порядок частот характерен для парциальных ядерных колебаний, активно формирую

щих надатомные структуры в среде. Таким образом, на- датомные структуры и физико-химическая активность ионов существенным образом зависят от времени года, а фиксируясь в морфогенетических структурах в период развития индивида, определяют его индивидуальность. С другой стороны, этим же обстоятельством обусловлена и определенная типичность, то есть схожесть по некоторым признакам, индивидов, зародившихся в одно и то же время года, но в разные годы.

Вариации резонансных частот среды происходят не только под воздействием годичного цикла, но и ряда других. Например, суточная вариация скорости тела, находящегося на экваторе планеты, приводит к вариации кинетической энергии на величину порядка 3 %. Отсюда следует, что в единицах частоты это Av = (2тУзУ,) / h.

— экваториальная скорость — имеет величину около 450 м/с, следовательно, Av для протонов составляет примерно 7 X 10’^ Гц, что, опять же, попадает в полосу ионных резонансов. Суточная вариация скоростей существенно зависит от щироты, стремясь к нулю в полярных областях. Следовательно, индивидуальность минерала или биологической особи определяется не только временем, но и местом зарождения.

Следует отметить, что помимо рассмотренных механизмов вариации частот плазмоподобных резонансов за счет годового и суточного движения планеты безусловное значение имеют и вариации, связанные с положением масс в Солнечной системе, то есть фактически с положением планет. Если нас интересуют более длительные эпохи развития минерального или живого царств, то положение Солнечной системы в Галактике, в связи с существенной неоднородностью распределения в ней масс, та1сже приводит к вариациям скоростей, а следовательно, к изменению хода процессов формирования надатомных структур.

Из рассмотренного выше следует, что существует возможность управления тонкими структурами мезо- уровня с помощью выбора времени и места осуществления процесса получения вещества с заданными свойствами. Возможна также механическая активация процесса путем осуществления его в подвижных средах или движущихся реакторах.

Механический контроль процессов может быть усилен или ослаблен в присутствии магнитных и механических полей. Например, воздействовать на структуру электропроводных сред электрическим полем не представляется возможным, однако сочетанное действие магнитного поля и механического движения среды делают это реальным. Наиболее известным примером использования механо-магнитной активации являются устройства омагничивания воды, подающейся в водогрейные установки, за счет которых предотвращается образование накипи на теплообменных поверхностях.

Возможно, что астрологическая типизация индивидов основана в неявном виде именно на рассмотренных механизмах формирования индивидуальных структур. Но эта проблематика, как и детальный анализ индивидуальных мезоструктур и влияния их на макросвойства вещества, выходит за рамки данной работы.

ЛАЗЕРЫ

Методология исследования сред, способных усиливать оптическое излучение и пригодных для создания

ИСТОЧНИКОВ когерентного излучения, основана преимущественно на принципах квантовой механики и в основном успешно себя оправдывает. В то же время, оперируя категориями статистически вероятных состояний, квантово-механический подход «совсем не интересуется» процессом перехода из одного состояния в другое и выводит его за рамки познаваемого. Вместе с тем главное достоинство лазерных систем заключается в когерентности излучения, что само по себе подразумевает наличие кооперативного механизма перехода из одного состояния в другое. Во многих практических и теоретических случаях эта «философия» неактуальна. Но если взять наиболее эффективные оптические активаторы, то окажется, что их совсем не много. Элементарных всего два. Это хром и неодим, которые «хорошо себя ведут» во множестве матриц.

Механизмы оптической активности хрома и неодима существенно различаются, как и особенности их вхождения в матрицы. На естественно возникающий вопрос: «Почему всего два?» — ответить достаточно сложно, если не вспомнить об их магнитных, точнее, антиферромагнитных, свойствах. Только эти два элемента имеют температуру перехода в антиферромаг- нитное состояние существенно выше комнатной. Все иные известные активаторы испытывают антиферро- магнитное упорядочение при весьма низких температурах, а соответственно, и «работать» начинают при столь же экзотическом охлаждении. Существуют, однако, и иные антиферромагнетики с высокой температурой упорядочения спиновых решеток. Например, монооксиды никеля, кобальта и железа. Их тоже не много. Наличие антиферромагнитных свойств у активаторов переводит лазерно-активные среды в разряд систем с упорядоченной мезоструктурой. Естественно предположить, что как раз это обстоятельство и определяет когерентный механизм запуска оптического перехода с помощью малозаметного по энергии управления магнитными (спиновыми) волнами.

Можно также предположить и иной механизм когерентного запуска с помощью механического поля фоно- нов, который, возможно, реализуется в активированных стеклах и жидкостных элементах.

Оптические явления в лазерно-активных средах наиболее отчетливо демонстрируют кооперативный характер процессов в конденсированном веществе, подчеркивая значимость мезоструктурных уровней его организации. Действительно, когерентный отклик оптически активированных сред автоматически подразумевает наличие когерентной структуры с линейными параметрами, соответствующими или соразмерными длинам волн генерируемого (или усиливаемого) излучения. Традиционные ныне методы описания, к сожалению, этой связи не вскрывают, а результаты оптического исследованР1я сред с явно выраженными когерентными свойствами интерпретируются в духе статистических (вероятностных) подходов, в свою очередь, подразумевающих интимный характер взаимодействия ионов с электромагнитным полем, хотя влияние окружения, как правило, очевидно.

Обнаруженные в процессе экспериментальных исследований щелочно-галоидных кристаллов с центрами окраски закономерности не нашли адекватного квантово-механического описанР1я, что можно было бы приписать некомпетентности автора. Но, с другой

стороны, вся совокупность этих методов не указывает рецептов понимания локальной перестройки надатом- ных структур кристаллов в процессах аддитивного или радиационного окрашивания. И именно эти проблемы приходится решать при создании оптически активных сред. Поэтому имеет смысл более детальный анализ процессов в хорошо изученных системах, типа корунда, активированного ионами хрома.

Лазер на рубине генерирует излучение в красной области видимого спектра на двух линиях люминесценции: сХ = 0,6943 мкм и Я, = 0,6929 мкм. Возбуждение рубина осуществляется в широких пределах «зеленой» и «синей» полос с максимумами при 0,56 мкм и 0,41 мкм соответственно. Мезоструктуры этого порядка, как показано выше, индуцируются электронами, «амплитуды» которых можно определить из классического выражения для энергии осциллятора:

Е = mAW/ 2,

которая, с другой стороны, находится из адиабатического инварианта

где h — постоянная Планка. «Полное» приращение частоты дает Е = ho, откуда

что дает хорошее совпадение с размерами ближайшей координационной сферы хрома, в которой находятся шесть ионов кислорода.

Поскольку из приведенного выражения следует также, что

А2~Я,

так как

то можно считать, что длины волн, или, точнее, линейные размеры соответствующей мезоструктуры, пропорциональны площади контура «распределения» электрона. А так как последний «распределен» на шести ближайших ионах, то при «распределении» его на произвольном числе п ионов соответствующие длины волн связаны выражением

или

Полученное выражение справедливо в случае, когда в ближайшей координационной сфере находится шесть равноправных ионов, а следовательно, применимо и для шелочно-галоидных кристаллов с кубической симметрией. Наиболее коротковолновая полоса рубина (к = 0,41 мкм) обязана своим происхождением оптическому электрону ближней координационной сферы. В формировании его «зеленой» полосы (А. = 0,5 мкм) «повинен» электрон, «распределенный» на восьми ионах. Для этого должны сушествовать дополнительные условия «дефектности» кристалла, поскольку восемь катионов не отвечают «правильным» координационным сферам. Нетрудно определить и число ионов, на которых распределен «возбужденный» электрон: п = /\ = (6х 0,694) / 0,41 « 10.

Наряду с мезоструктурой, индуцированной «дефектными» оптическими электронами, в рубине сушеству- ет также ряд других виртуальных структур, заданных парциальными частотами ядер. Это в первую очередь две структуры с размерами, сушественно меньшими одного микрометра, обусловленные кооперативными колебаниями ядер кислорода и алюминия. Самое поразительное состоит в том, что эти струьсгуры по размеру своих периодов соответствуют полосам поглоще- ния рубина! Разностная частота парциальных колебаний ядер кислорода и алюминия образует структуру с периодом около 1,5 мкм. И, наконец, ядра хрома, осциллируя, индуцируют структуру в миллиметровом диапазоне. Для оценки частот использовались изложенные в предьщущей главе соображения о резонансах в плазмоподобных средах.

Следует отметить и еще одно важное обстоятельство в кооперативных процессах. Виртуальная мезострук- тура, индуцированная «возбужденными» электронами, может быть представлена как структура из виртуальных частиц с характерной частотой лазерного перехода. Можно определить массу такой частицы из равенства

тс^ = hv.

Учитывая, что линейные размеры частицы определяются половиной длины волны, оценим концентрацию как

Приведенный заряд виртуальной частицы определяется суммой всех когерентно движущихся зарядов в пределах «шубы» толщиной дебаевского радиуса, то есть практически всех оптических электронов. При концентрации активирующей примеси порядка 10’’ см ‘ в виртуальной частице с X, = 0,7 мкм число зарядов будет:

Z= 10^

Следовательно, плазменный резонанс соответствует частоте v = (ne^Z^/ значительно превышающей оптическую и близкой к частоте ядра. Этот резонанс может приводить к возбуждению рентгеновского и гамма-излучений. Причем не обязательны условия возбуждения оптической генерации. Можно показать, что виртуальные структуры миллиметрового и сантиметрового диапазона также могут являться источником жестких излучений при возбз^ждении резонанса в соответствующем диапазоне.

Вьивленная связь между длинами волн в спектрах поглощения и люминесценции, с одной стороны, и характерными размерами области распределения оптических электронов — с другой — первоначально была определена из анализа экспериментальных данных по значительной группе щелочно-галоидных кристаллов с центрами окраски. Оказалось, что отношения длин волн, соответствующих максимумам полос поглощения и обусловленных центрами окраски, к длине волны наиболее коротковолновой F-полосы образуют компактные группы значений.

Кристалл

Полоса

М

N

NaCl

1,21

1,32

1,57

1,83

КС1

1,22

1,35

1,49

1,78

КВг

1,22

1,31

1,48

1,78

KJ

1,22

1,36

1,54

1,86

NaF

1,18

1,31

1,50

RbBr

1,20

1,29

1,48

LiF

1,22

1,52

1,76

2,28

В различных кристаллах наблюдается замечательное согласие идентификации полос, за исключением фтористого лития, для которого, вероятно, существ)чот проблемы интерпретации.

Объяснение столь согласного поведения спектров щелочно-галоидных кристаллов с центрами окраски состоит в том, что оптические электроны одноименных полос «распределены» на одинаковых количествах катионов ближних к дефекту координационных сфер. Поскольку щелочно-галоидные кристаллы относятся к кубической группе симметрии, то ближайшее окружение аниона или анионной вакансии представлено шестью катионами. Отсюда, как и в предыдущем случае,

X =(п/6)хХ,.

Так, например, для хлористого калия с F-полосой при 540 нм можно сопоставить достаточно хорошо известный спектр:

Таблица 4.4

Положение полос в спектре хлористого калия

п

Расчет по F-полосе

Экспериментальные данные

X , нм

max’

X , нм

max’

Название полос

1

90

2

180

187

к

3

270

253

4

360

338

L,

5

450

457

К

6

540

F

7

630

657

R,

8

720

728

R.

9

810

805

М

10

900

11

990

968

N

Найденная закономерность позволила поставить вопрос о правильности идентификации полос, но самое важное то, что стало возможным достаточно наглядное представление структуры F-агрегатных центров, а следовательно, и целенаправленное их «конструирование».

Полосы, более коротковолновые по сравнению с F-полосой, традиционно приписывались переходам на высшие энергетические уровни. На самом деле оказалось, что они соответствуют центрам с «неполным» числом «дефектных» катионов.

Детальное рассмотрение моделей центров F-arpe- гата выявило ряд совершенно новых особенностей их структуры и эволюции. Большую роль в спектре полос играют центры некомпактной структуры. Старение центров ведет к увеличению их компактности. Поглощение в М^-полосе для фтористого лития обусловлено вовсе не ионизованным двойным центром, как считалось ранее, а совокупностью «рыхлых» центров, компакти- зация которых ответственна за смещение М’^-полосы в коротковолновую сторону. Сохранить некомпактную структуру соответствующего центра, интересного своей способностью к генерации излучения в области 910 нм, можно просто вводя в кристалл примесь таких анионов, подвижность которых меньще подвижности фтора. Например, ион гидроксила — ОН”. Это решение, наряду с выбором оптимальной температуры окрашивания, позволило создать устойчиво и эффективно работающие активные элементы. К аналогичному результату приводит и радиационное окрашивание кристаллов потоком протонов. Дело в том, что кислород в кристаллах фтористого лития есть практически всегда, а его объединение с протонами и дает образование ионов гидроксила. Кроме того, протонное окрашивание позволило создать очень высокую плотность центров окраски. Активные элементы из окрашенных протона-

МИ кристаллов также показали эффективную работу. Благодаря высокой плотности центров окраски, образующихся при протонном облучении, этот метод окрашивания имеет большие перспективы для оптической записи информации и в качестве активных элементов с распределенной обратной связью.

Первым шагом в образовании агрегатных центров окраски F-типа является, очевидно, присоединение к F-центру свободной анионной вакансии. Количество «дефектных» катионов вокруг двух соседних вакансий, расположенных на оси (100), равно 10, а вдоль (ПО) — 11. Согласно выражению = (п / 6) х Хр получается, что F2^-цeнтpы должны поглощать в области М-полосы. Однако соответствующие наблюдения полосы показывают, что она является более длинноволновой и может быть обусловлена распределением электрона на 14 и более катионах. Такая ситуация реализуется, если вакансии не являются непосредственными соседями. Вероятность обобщения электроном двух таких вакансий не вызывает сомнения, поскольку распределение его, обладая значительной диффузностью в F-центре, охватывает несколько координационных сфер. Можно отметить также несколько характерных деталей, подтверждающих такую модель F2^-цeнтpoв. Соответствующая полоса поглощения при температурах подвижности анионных вакансий исчезает, но одновременно возникают полосы, соответствующие центрам с 10 либо 11 катионами. Эту трансформацию принято объяснять, вслед за Делбе- ком, нейтрализацией F2^-цeнтpa путем захвата второго электрона. Источники последних, как правило, не называются. В нашем случае объяснение не требуется вовсе, так как Р^^-центр представляется промежуточным состоянием в процессе сближения обобщенных электроном вакансий. Большая ширина М’^-полосы хорошо согласуется с разнообразием позиций возможного соседства вакансий на разных этапах их сближения, а следовательно, и с некоторой неопределенностью в размерах катионной подсистемы центров. Необычное смещение М’^-полосы в коротковолновую сторону при увеличении температуры кристалла находит достаточно простое объяснение: каждый шаг вакансии при сближении сопровождается уменьшением числа «дефектных» катионов и характеризуется смещением поглощения в «синюю» область, не выходя поначалу за пределы М^-полосы. Длинноволновая компонента полосы тем самым ослабляется, и происходит наблюдаемый сдвиг максимума. Переход вакансий в состояние непосредственного соседства, в отличие от предыдущих актов сближения, сопровождается значительным изменением катионной подсистемы, и центр начинает проявлять себя в области N-полосы.

Все сказанное выше относится к кристаллам без примесей. Примеси, как анионо-, так и катионозамещающие, вносят существенные искажения в решетку кристалла и, располагаясь рядом с центрами окраски, являются их структурными элементами. Ионы щелочноземельных металлов входят в кристалл галогенидов щелочей, создавая необходимость появления катионных вакансий. Катионная подсистема модифицированного такой примесью центра будет обеднена, и оптический переход станет более коротковолновым по сравнению с переходом невозмущенного центра. Одновременное наличие тех и других центров для диффузной М^-по- лосы проявляется в смещении ее максимума в коротковолновую сторону спектра и неэлементарности кинетик появления и исчезновения поглощения. Присутствие во второй координационной сфере, для анионной вакансии центра, инородных анионов с больщими энергиями активации подвижности затрудняет подход к ней других анионных вакансий. Этот дефект при наличии электрона проявляется в М^-полосе с повышенной термической стабильностью.

Нейтрализация Р^^-центра, то есть присоединение второго электрона, — событие достаточно вероятное при воздействии на кристалл ионизирующей радиации. Движение двух электронов в центре окраски, удовлетворяя принципу Паули, может осуществляться по той же катионной подсистеме, что и движение одного. Следовательно, значительного измененры частоты оптического перехода при нейтрализации центра может и не наблюдаться.

Две рядом расположенные анионные вакансии имеют ближайшее окружение, состоящее из 10 или 11 катионов. Согласно выражению

X =(п/6)хХ,

полосы, соответствующие центрам с такой катионной подсистемой, имеют максимумы в области, традиционно приписываемые более агрегированным центрам. Однако полоса двойных центров в кристалле фтористого лития находится как раз в этой области. На первый взгляд представляется, что «один кристалл идет в ногу, а остальные не в ногу», так как поглощению двойных центров в них соответствует полоса, которая может быть обусловлена 9-катионной подсистемой. Кристаллы фтористого лития тоже имеют в этой области полосу, приписываемую тройным центрам. Эта полоса обычно менее интенсивна по сравнению с М-полосой. Катионная подсистема центра из двух анионных вакансий может состоять из девяти катионов, если в состав его входит еще и катионная вакансия. Такой вывод согласуется с моделью центра М-полосы, предложенной в свое время Зейтцем. Отличие кристаллов фтористого лития от остальных заключается, видимо, в том, что вероятность образования бивакансий в нем ниже. Это обусловлено, возможно, малым радиусом иона лития. Аналогичная ситуация наблюдается для кристаллов хлористого лития.

Влияние катионной вакансии может иметь место и в случае F-центра, поскольку его катионная подсистема будет состоять из пяти ионов и полоса поглощения сместится в коротковолновую сторону. Поглощение центра с пятикатионной подсистемой соответствует известной К-полосе.

Заполнение электронами положительно заряженных дефектов в кристалле принципиально отличается от распределения их в атомах вследствие различий в структуре тяготеющих центров. Заряд атома сосредоточен в ядре, а электроны формируют энергетические оболочки в соответствии с принципом Паули. Электронам центра окраски, положительный заряд которого рассредоточен на катионной подсистеме, может оказаться энергетически выгодной локализация только на части катионов, удовлетворяющая принципам электронейтральности.

Два электрона, как отмечалось, могут совершать согласованное по спину движение по одной катионной подсистеме. Появление третьего электрона не дает начало следующей оболочке, как в атоме, хотя и такой вариант нельзя исключить, а приводит к разделению катионной подсистемы на две относительно самостоятельные. Число дефектных катионов тройного центра равно 13 и более. Разбиение такой системы на две группы с примерно одинаковым количеством катионов может дать числа 6 и 7, например, что соответствует поглощению в F- и Rj-полосах.

Возбуждение тройного центра в любой из полос всегда связано со значительной перестройкой его электронной структуры. Отход одного из электронов приводит к «заселению» двумя оставшимися всей катионной подсистемы. Следствием перестройки является одновременное просветление кристалла в сопряженной полосе, а также появление наведенного поглощения в длинноволновой области спектра. Например, центр, поглощавший в R’- и R^-полосах, что соответствует дефекту с суммарной катионной подсистемой 15 катионов, при воздействии света в R‘- или R^-полосе может проявить себя поглощением в М’^-по- лосе. Так как поглощение тройных центров имеет место не только в характерных R’- и R^-полосах, но и во многих других, если не сказать «во всех остальных», то становится понятной чувствительность всего спектра кристалла с центрами окраски к спектрально-селективному фотовоздействию.

Экспериментальное изучение описанных свойств центров окраски возможно методами лазерной спектроскопии высокого временного разрешения.

На рисунке 4.4.1. изображены возможные области локализации электронов в нейтральном тройном центре, находящемся в основном в возбужденном состоянии.

Рис. 4.4.1. Области локализации электронов в тройном центре F-типа: а) основное состояние; б) возбужденное состояние

Обсуждение моделей центров окраски показывает, что строго однозначная идентификация спектров поглощения кристаллов в общем случае не имеет смысла. Ответственным за конкретную полосу поглощения может быть большой набор дефектов, изучение которых требует привлечения разнообразного экспериментального материала.

Проведенный анализ подчеркивает динамичную природу окраски кристаллов и органическое единство его спектральных свойств. Следует также отметить, что довольно абстрактный подход, положенный в основу анализа, не приводит к расхождению с выводами из колоссального объема скрупулез1п»1х экспериментальных исследований, но может служить пониманию деталей структуры центров окраски и особенностей рк поведения.

Всякому дефекту соответствует искажение кристаллической решетки в области хотя и атомного масштаба, но значительно превышающей размеры первоисточника. «Заряд анионной вакансии» не сосредоточен в ее центре и не распределен даже на катионах ближайшего окружения. Отсутствие ионной связи частично восполняется усилением взаимодействия дефектных катионов с анионами следующих координационных сфер. Таким образом, нескомпенсированный заряд рассредоточен на существенно большем количестве катионов.

Локализация электрона в области распределения положительного заряда компенсирует отсутствие ионной связи и меняет структуру самого распределения. Заряд в этом случае почти полностью сосредоточен на катионах ближайшего окружения анионной вакансии. Вначале электрон движется по катионам, принимавшим участие в компенсации заряда, и лишь затем, отдав часть энергии на устранение деформации решетки, — по истинно дефектным катионам.

Описание оптического перехода, сопутствующего локализации электрона проводимости на положительно заряженном дефекте, может быть построено на тех же основах, что и описание перехода в F-центре. Считая по-прежнему «частоту» локализованного электрона зависящей от числа катионов, но не ближайщих, а всех принявших основное участие в распределении неском- пенсированного заряда, можно считать А,= (п / 6) X А,. ,

посколысу отсчет энергии ведется от дна зоны прово- димости. Определение числа катионов в данном случае представляет не тривиальную задачу, однако некоторые выводы могут быть сделаны в общем виде. Так как последнее выражение не отличается от полученного для переходов центров окраски и в обоих случаях отсчет ведется от зоны проводимости, то полосы рекомбинационного свечения должны совпадать с теми или иными полосами поглощения центров окраски, поскольку числа целые. Хорошо подчиняются этому правилу полосы термостимулированой люминесценции и свечения под действием рентгеновского излучения.

Движение возбужденного электрона центра окраски мало отличается от его движения в зоне проводимости, поэтому сказанное выше можно распространить на обратные оптические переходы (люминесценцию) центров. Ниже приводится таблица с данными по положению максимумов полос погаощения и люмршесценции кристаллов фтористого лития с центрами окраски. Из таблицы 4.5 следует, что практически каждому набору катионов соответствует как полоса поглощения, так и излз^ения.

Возбуждение центра окраски, связанное с отходом электрона от него на довольно значительное расстояние, сопровождается изменением распределенрм положительного заряда и деформации решетки кристалла. Более того, время жизни возбужденного состояния столь велико, что вакансии центра могут совершить до десятка переходов из узла в узел. Перестройкой конфигурации взаимного расположения анионных вакансий во время возбуждения центра можно объяснить во многих случаях изменение его оптических свойств.

п

X, НМ

Известные полосы, нм

поглощения

излучения

6

250

250

253

7

292

286

8

333

320

9

375

380

387

10

417

420

413

11

458

458

459

12

500

500

506

13

542

550

530

14

583

570

15

625

620, 645

620

11

Х, нм

Известные полосы, нм

поглощения

излучения

16

667

660

670

17

708

700

690

18

750

740

19

792

790

20

833

22

917

910

23

958

960

27

1124

1120

Данный подход можно перенести на другие ионные кристаллы, учитывая особенности их структуры и характера «движения» в них электронов.

СИЛИКАТЫ

Рассмотренные выше мезоструктуры в лазерноактивных средах, как, впрочем, и в материалах микроэлектроники, имеют важнейшее функциональное значение. Однако их прямое наблюдение представляет достаточно сложную техническую задачу. Стеклокристаллические материалы, напротив, предоставляют возможность прямого наблюдения при микроскопическом их исследовании за счет эффекта автодекорирования собственных полей стекла кристаллическими агрегатами.

Кооперативный характер процессов в среде приводит к сушественной неоднозначности причинно-следственных связей. Выше, например, было показано, что процесс упорядочения может иметь направление от низкочастотных, то есть низкоэнергетических, структур к высокочастотным. Хотя на первый взгляд это противоречит логике подчинения слабого сильному. Подобная схема кажется и вовсе не применимой к явлениям образования надатомных структур. И, тем не менее, го-

раздо чаще структурой химического масштаба, то есть порядком ионных связей, управляют кооперативные мезоструктуры. Это наиболее выпукло проявляется в явлениях изоморфного замещения, когда общий структурный мотив среды «расставляет» ионы таким образом, какой порою невозможно представить. И вместе с тем эти эффекты можно широко использовать в получении материалов с перспективными свойствами.

Дело в том, что ничего алогичного здесь нет. Действительно, энергия надатомных струюур, как правило, на порядки меньше энергии ионных связей. Но, во-первых, можно вычислить энергию взаимодействия, однако само оно осуществляется не энергией, а полем силовой природы. Суперпозицрм напряженностей поля есть вектор. Энергия скалярна. Поэтому даже в простейших случаях интерференции решение задачи из энергетических соображений невозможно. И, во-вторых, количество элементов в низкочастотной структуре на те же порядки больше числа ионов, взаимодействующих «химическим» образом. Поэтому напряженность интегрального поля надатомной структуры в больщин- стве случаев сопоставима с силами ионного взаимодействия, если не превышает их.

Напомним вкратце полученные выше выводы. Колебания ядер в электронном окружении с частотами 10 ‘ 10′ ’ Гц порождают объемные стоячие волны (фигу

ры Лиссажу) с длиной, соответствующей атомным размерам ~10 ‘® м. В пучностях этих волн находятся электроны атома, колеблющиеся с частотами 10’Гц. Осцилляции электронов возбуждают стоячие волны с субмикронными размерами. В этот же диапазон попадают и волны, генерируемые парциальными колебания-

МИ ядер. Когерентное движение электронов, например, в поле этих стоячих волн с частотами порядка 10’^ Гц является вынужденным, с амплитудой

А^ = 2Е/(тю„2),

где — частота вынуждающего поля;

Е — энергия установившихся колебаний, которая может быть определена из адиабатического инварианта Е/© = h, тогда

= 2h / (m^toj.

Но из этого выражения следует также, что при данной амплитуде и энергии, определяемой из адиабатического инварианта, возникают новые колебания с частотой

®„зл = 2Ь/(тА^),

причем в знаменателе может находиться либо масса электронов, либо ядер. В первом случае имеем тривиальный результат: = ©^, то есть электроны, со

вершающие вынужденные колебания, излучают с частотой вынуждающего поля. Однако в другом случае: © =(m/m)© — возникает излучение с частотой

меньщей на три с лишним порядка. Например, в большинстве случаев в качестве ядра можно считать протон, с )щетом того, что водород — наиболее распространенный элемент во Вселенной, тогда © = © / 1836. Конечно,

эти значения будут с)чцественно отличаться для веществ, где водород не играет определяющей роли. Излучение с частотой ©^^, будучи кооперативным по природе, также образует стоячие волны, и последнюю формулу можно использовать как рекуррентную для определения иерархии структурных пространств атома, и далее, полагая размеры их равными полудлине соответствующих волн, в ряду = (1836)” X Л,д. Ниже, в таблице 4.6, приводится этот идеализированный ряд по водороду.

п

Частота (Гц)

X / п (м)

Условные представители

0

10”

1,5 X 10″

атом

1

5 X 10”

3 X 10*

прима-тело, мицеллы

2

3 X 10”

0,5 X Ю-’

1слетки биологических тканей

3

1,6 X 10’

-1 X 10-‘

животные, растения, рудные жилы

4

0,87 X 10^

1,7 X 10^

5

4,7 X 10^

0,31 X 10«

6

2,56 X 10-‘

0,6 X 10’

Солнце

7

1,4 X Ю”*

10”

орбита Юпитера

8

0,76 X 10-’

2 X 10”

световой год

9

4 X 10″

3,7 X 10”

ядро Галактики

Естественно, что для любых других ядер этот ряд будет изменяться значительно быстрее. Например, для оксидных систем существенны частоты и струюуры, обусловленные кислородом. Тогда \ = (16х 1836)”

Частота (Гц)

А. / 2 (м)

0

4 X 10”

3,7 X 10-”

классический электрон

1

1,36 X 10”

1,1 X 10’

110 нм

2

0,46 X 10″

3,24 X 10-3

3,24 мм

3

1,56 X 10*

10’

100 м

То есть наиболее существенными становятся мезо- структуры субмикронного (110 нм) и миллиметрового диапазонов. Именно эти «пространства» контролируют кристаллизацию хромшпинелида. На рисунке 4.5.1 представлено электронно-микроскопическое изображение начала процесса кристаллизации, где отчетливо видны мицеллы (0,1 мкм), организующиеся в «рещетки» миллиметрового размера.

пространства:

Са

Mg

Na

A.J, нм

174

130

130

Х-2, мм

12,8

5,6

5,5.

Для систем, содержащих кремний, также важны и «пространства» с размерами несколько большими «кислородных»: 1,4 х 10’’ м и 7,4 х Ю’^ м. Наиболее часто встречаются (и исследуются в настоящей работе) силикаты, включающие в свой состав оксиды кальция, магния и натрия. Для этих элементов соответствующие

Таким образом, в спектре структурных образований силикатов доминантными являются мезоструктуры с характерными размерами И (К 174 нм, агрегированные в «гранулы» 3^13 мм. Посю)льку мы имеем дело всегда с набором частот, то в спектре размеров непременно фигурируют и комбинационные компоненты. Например, комбинация мезоструктурных частот кислорода и магния генерирует «пространство» размером порядка 2 мкм, а близкие частоты натрия и магния формируют структуру с

Ось щмтмылм- Мали

/

Р=Е хН.

Рис. 4.2.1. Интерференция колебаний с большим отношением частот суперпонируемых волн

Таблица. 4.2

Типы когерентности и общая классификация материалов

ДуАх > 1

Аг>1/(1/Х2-1/Х,),

30 км/с Земля

230 км/с

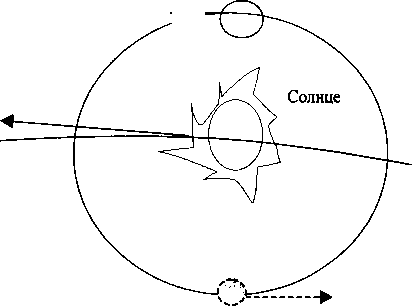
Рис. 4.3.1. К годичной вариации кинетической энергии

Отсюда вариация кинетической энергии любого тела на поверхности нашей планеты варьирует относительно среднего значения на существенную величину

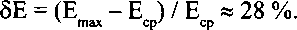
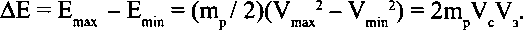
460 м/с

Земля

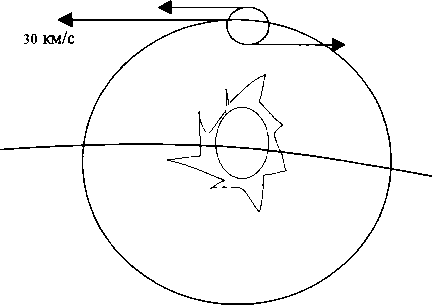
ДЕ/Асо = h,

A = (2h/(mcй))”^

1/со = Я / (2лс),

X ln = XJ6

X =(п/6)хХ,.

п = 8 / Х,^.

Таблица 4.3

Положение полос поглощения F-агрегатных

центров относительно F-полосы

с центрами окраски

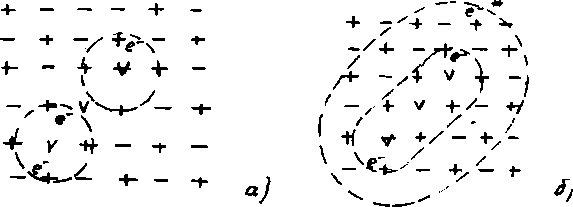
Таблица 4.5

Таблица 4.6

Иерархия пространств

Рис. 4.5.1. Начало кристаллизации базитового стекла

Рис. 4.5.2. Пространственно-ритмическая структура многоэтажных седло- видных золото-кварцевых жил (Бендиго, Австралия), образованных в результате сброса напряжений. Расстояния между антиклиналями и жилами в них соответствуют волновым числам установившихся колебаний в вертикальном направлении по оси образовавшегося в результате сброса напряжений волновода, ограниченного горизонтальными поверхностями рудовмещающей толщи. Наиболее интенсивные жилы соответствуют кратному делению длины волновода, располагаясь по- средине и на расстояни- ‘ ях в четверть его длины. 1 — сланцы и песчаники;

Глубина ЮЭм

О SO \20

Усть« 1^гиты Hi i6c отм

Уромяь мторй

\В0 201м

1 2 — рудные жилы;

3— сдвиги;

1. — дайки мончикита.

   Приведенный анализ не исчерпывает всех деталей структурного спектра, поскольку не рассмотрены еще особенности электронных и парциальных ядер- ных частот. Например, последние для ядер кислорода формируют структуры с размерами около полутора микрометров, что порождает «пространство» следующего порядка с периодом 45 мм. Итак, помимо собственно ионной структуры, традиционно считающейся кристаллической, силикаты обладают и более укрупненным порядком, явным образом не связанным с кристаллическим. Более того, очень часто развитие структур дальнего порядка опережает формирование мезоструктур и, вероятно, определяет характер ближнего порядка. Это подтверждается приведенным выше электронным снимком кристаллизирующегося хромшпинелида (рис. 4.5.1), где кристаллизующиеся фрагменты имеют вполне закономерную ориентацию. На серии снимков стекла волластонитового и пироксенового составов (рис. 4.5.4) наблюдаются явные признаки дальнего порядка «при полном отсутствии ближнего».

   «Обратный» механизм эволюции порядка уже рассматривался выше. Далее будет показано, что при формировании тектонической структуры облика планеты региональные (высокочастотные) признаки вторичны по отношению к глобальным — низкочастотным. Отмечалась также возможность генерации жестких полей кооперативными структурами среды. Подобный механизм реализуется и при упорядочении вещества.

   «Прямое» упорядочение среды при потере ею энергии, например, при медленном охлаждении

периодом в треть метра, что существенно лишь для крупных образцов. Тем не менее, структуры метрового и более масштабных диапазонов не так уж трудно наблюдать. Например, рудные тела очень часто представляют собой именно периодические структуры (рис. 4.5.2, 4.5.3).

Рис. 4.5.3. Периодическая структура око- лорудного изменения пород, обусловленная волновыми процессами в замкнутом пространстве рудного тела (по Рундквисту)

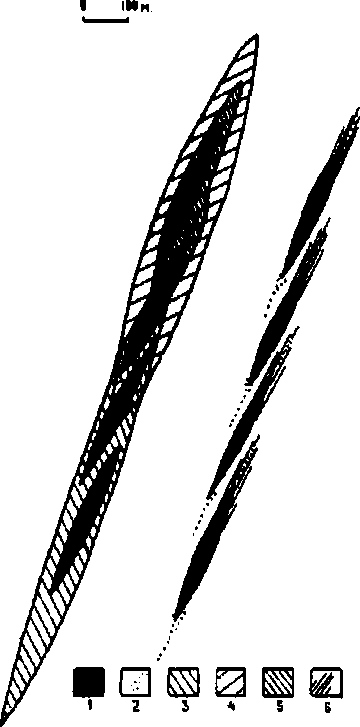
1. —рудные тела;
2. — вкрапленность магнетита;
3. — эпизотизация;
4. — хлоратизация;
5. —пироксенизация;
6. — имфиболизация.

Когерентное движение ядер среды, помимо генерации низкочастотного поля следующей пространственной иерархии, сопровождается и новой высокочастотной компонентой. Если частота когерентного движения V, то из адиабатического инварианта энергия, с ним связанная, — Е = hv.

Эта величина является полной энергией виртуальной частицы с массой т^, определяемой из закона Е = ш^с^.

Масса виртуальной частицы при низких частотах мала, например, уже при частотах парциального ядер- ного резонанса v = 10’^ Гц

Концентрация виртуальных частиц тоже невысокая: п ~ 1 / = (v / с)^»10’^ м ^

Но величина когерентно движущегося в пределах виртуальной частицы заряда весьма значительна Z = X^xn„Z„/8 = (cVv^)xn/^/8, здесь Пд — концентращ1я ионов данного сорта с зарядом ядра Zp.

Для плазмоподобного резонанса v

Для среды с водородом Z^ = 1, ~ 10^’ м= v при

Плазмоподобный «обратный» резонанс виртуальных частиц может определять не только характер структуры субатомного пространства, но и направленность химического взаимодействия, что реализуется в каталитических процессах. Участие виртуальных резонансов в последних будет существенным при > 10** Гц, то есть при энергиях, характерных для ионизации. Тогда при осуществлении процесса в трубных реакторах сантиметровых размеров или в образцах того же масщтаба, где v ~ 10*® Гц, необходимо наличие «примеси» с величиной

При высоких Пц, Zq и радиочастотном возбуждении в диапазоне 1 ГГц виртуальные резонансы соответствуют энергии в десятки килоэлектронвольт, то есть диапазону рентгеновского излучения, влияя на внутриатомные переходы либо излучаясь в пространство.

Небезынтересно отметить, что в резонаторе метрового диапазона можно возбудить резонансы с энергиями, соответствующими массе покоя протона. Однако объемная плотность энергии высокочастотных резонансов, возбуждаемых в сантиметровом и метровом диапазонах, невелика, и к тому же они не столь интересны в процессах структурирования сред, хотя могут играть значительную роль в космогонических процессах. Наибольший практический интерес, вероятно, представляют поля теплового диапазона, возбуждаемые в термических процессах. Для этих частот имеют значение собственные мезоструктуры среды миллиметрового диапазона, контрастные границы, вблизи которых возможно существование стоячих волн, и.

Резонаторы, обеспечивающие образование стационарных электромагнитных полей термического происхождения, — это в большинстве случаев собственные мезоструктуры силикатов. Например, на рисунке 4.5.5 ниже приведен электронно-микроскопический снимок стекла пироксенового состава в закаленном состоянии.

Совершенно отчетливо наблюдаются кольцевые структуры с размерами 10 мкм, 5 мкм и 2,5 мкм, про- декорированные мицеллами нанометрового диапазона. Каждое из этих колец является резонатором для те-

Развитие виртуальных резонансов существенным образом зависит от наличия резонаторов, которыми являются мезоструктуры, и от источника возбуждения, каковым обычно является нагрев образца. Для силикатов мезоструктуры миллиметрового диапазона, ответственных за взаимодействие с тепловым излучением, задаются колебания ядер кислорода и кремния. Характерные размеры их стоячих волн порядка 3,2 мм и 7,4 мм. Комбинационные структуры дают размеры порядка 5,7 мм и 2,3 мм. Поэтому при последовательном нагреве образца возникает по крайней мере четыре «обратных» резонанса с частотами, соответствующими длинам волн, сопоставимых с атомными размерами. Вследствие этого ближний порядок испытывает существенную перестройку при каждом резонансе, «под- тягивая» собственные электронные частоты к частоте, кратной резонансной. Поскольку отношения частот при каждом резонансе иные, то и конфигурация замкнутого электронного пространства меняется. Этим определяются существование полиморфов кварца и их последовательная смена при изменении температуры. Можно предотвратить образование того или иного полиморфа, не дав развиться соответствующему резонансу, например, при быстром изменении температуры.

Спектр полиморфов тройных систем, типа волла- стонита, имеет гораздо больше компонент, поскольку добавляются новая мезоструктура (12,8 мм) и соответствующие комбинационные. Хорошо известны полиморфы волластонита: а-, (3- и у-. В данном исследовании вьщелено несколько новых, среди которых один исследован детально. Структура его такова, что он подобен удвоенному вдоль длинной оси кристаллической ячейки Р-волластониту и имеет игольчатые агрегаты. Но удвоение длины ячейки происходит одновременно с вращением добавляемого объема. Поэтому по аналогии с известными формами органических соединений предложено назвать этот полиморф трансволластонитом. Условия образования трансволластонита мало чем отличаются от таковых для Р-волластонита. Но всегда он образуется при более высокой скорости нагрева стекла, что, видимо, позволяет избежать некоторой скрытой перестройки, происходящей при температурах ниже точки стеклования.

Наблюдать полиморфы в системах, содержащих дополнительно магний и натрий, становится затруднительным, поскольку частоты, ответственные за появ

ление мезоструктур, заполняют спектр более плотно, и развитие явно выраженных резонансов становится невозможным. Поэтому в стеклах пироксенового состава обычно наблюдаются плохообратимый экзогенный эффект при температуре 650^750 °С и кристаллизация в диапазоне 960-^1050 °С. Еще более устойчивы многокомпонентные системы, применяемые, например, для производства лампового стекла.

Анализ резонансных механизмов структурообразо- вания позволяет выработать достаточно общие и в то же время конструктивные подходы к пониманию природы структуры среды. Общность подхода состоит в том, что с единой позиции рассматриваются любые иерархии структуры от микро- к мезо-, макро- и мегауровню, с одной стороны, и — с другой — среды любого элементного состава. Новым является представление об управлении порядком микроуровня структурами мезо- и макромасштабов.

Глава 5.

расплава, в большинстве случаев не дает желаемых свойств получаемого материала. Это характерно не только для технологии силикатов, но и для металлургических процессов. Положительные результаты достигаются обычно с помощью повторной термической обработки после достаточно быстрого охлаждения исходного расплава. Смысл «обратного» процесса состоит в том, что упорядочение на ми- кроуровне происходит под прямым контролем макро- или мезоуровнего порядка, в результате чего и достигается наиболее когерентная структура вещества, обеспечивающая высокие технические качества материала.

m = (hv) / с^» 10” кг.

= (e^Z^n / (8„m))”V (2я) = eZ„n/(27Ev48,m)‘^^).

V » 10” Гц. Частота v может быть как собственной частотой среды, так и частотой внешнего поля, заданного.

например, резонатором. Здесь важно лишь то, чтобы поле было представлено стоячими волнами.

П/,= 1(Р,

при Zj, = 1 (водород) Пд = 10^’ м ^ то есть среда должна быть представлена только водородом. Очевидно, что никакого процесса здесь не будет. Однако можно управлять ходом химического взаимодействия в смеси углеводородов при наличии ионов с большим зарядом ядра. Например, при тех же условиях, но при Zq = 78 (платина) концентрация катализатора в смеси всего около одного процента. Увеличив на порядок размеры реактора и тем самым уменьшив управляющую частоту, концентрацию катализатора можно снизить на два порядка либо использовать более легкие катализаторы переходной группы.

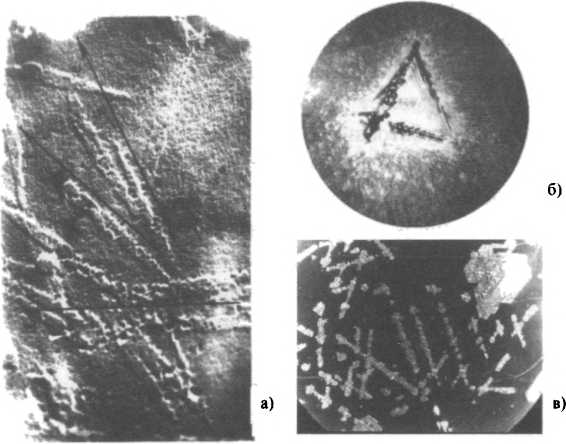
Рис. 4.5.4. Дальний порядок на начальных этапах кристаллизации волластонитового (а) и пироксенового (б, в) стекла (по Мананкову А. В.)

наконец, наличие примесей с ~ 10^* м ^ Эти

условия определяют характер субатомной структуры среды. Причем концентрация оказывается, как правило, в пределах долей процента, характерная, например, для многих металлов, включая сталь. Таковы же пределы концентраций «управляющих» примесей в силикатных стеклах. Наиболее характерно при этом влияние хрома на процесс кристаллизации стекол пи- роксенового и волластонитового состава. В обоих случаях происходит образование микрокристаллических агрегатов со случайной на первый взгляд ориентацией. Всегда, однако, наблюдается объемная кристаллизация, не имеющая явно выраженного фронта. По крайней мере, наблюдать его, как это удается в отсутствие хрома, не приходится даже в том случае, если оксид хрома находится лищь на поверхности образца толщиной до одного сантиметра. Столь сильное влияние хрома на процессы упорядочения силикатных стекол связано в немалой степени с его магнитными свойствами, поскольку когерентность движения в данном случае определяется не только кулоновским, но в первую очередь обменным взаимодействием.

плового излучения. При нагреве образца в резонаторе возникают стоячие волны, которые затем определяют и характер субатомного упорядочения.

Рис. 4.5.5. Структуры дальнего порядка в стекле (по Мананкову А. В.)

ПЛАНЕТА

ОБОЛОЧКИ

Непосредственному наблюдению и инструментальному исследованию доступна лишь ограниченная часть планеты, включая атмосферу, верхние слои земной коры и толщу поверхностных водоемов. В отношении других деталей планеты доступным является только теоретический анализ разнообразных гипотез, выдвинутых на основе особенностей механики небесного движения, результатов сейсмических исследований и обобщения данных по режимам и составам флюидов земной коры. Тем не менее, сложилось устойчивое мнение о наличии внутренних оболочек в структуре планеты, подкрепленное данными низкочастотной сейсмологии. Помимо коры различают мантию, внутреннюю мантию, ядро и внутреннее ядро.

Основой процессов в недрах планеты считается гравитационное взаимодействие. Пользуясь только этим соображением и даже учитывая разогрев как результат гравитационного сжатия, сделать какие-либо выводы о природе внутренней структуры достаточно проблематично. Можно предположить, что ответственными за структуру планеты является гравитационная сегрегация вещества в период аккреции и последующая термодиффузионная дифференциация. Однако такой подход не вполне состоятелен по кинетическим соображениям и перечеркивается сравнением с планетами, отличающимися плотностью и массой. Здесь можно возразить, что предыстория планет различных групп неизвестна. И далее на каждое возражение искать аргументы, а на любые аргументы всегда отыщется возражение.

Правомерно обсудить некоторые детали структуры планеты на основе соображений о неустранимости колебаний, особенно характерной для наиболее низших мод. Колебания геоида описываются сферическими гармониками. Последние всегда можно разложить по естественному ортогональному базису и в некотором приближении, для простоты анализа, рассматривать по отдельности тот или иной тип колебаний. Естественным базисом для геоида являются направления радиальных и тангенциальных колебаний, которые также могут быть разложены на ортогональные, в пределах отдельной оболочки. Представляется важным подчеркнуть, что роль радиальных колебаний в формировании оболочечной структуры может оказаться рещающей. Рассмотрим продольные колебания со сферическим волновым фронтом, нормаль к которому совпадает с радиусом планеты. Для гомогенного тела с размерами и массой планеты, при скорости распространения колебаний порядка 10″ метра в секунду, наиболее низкочастотные колебания в форме стоячей волны изменения плотности определятся из условия У! = откуда следует, что плотность изменяется с периодом х = Х! с X 1,3 х 10^ с, причем максимум амплитуды находится в центре тела. Относительно источников возбуждения колебаний с периодом около 20 минут можно предположить, что ими могут быть, на-

Наличие узловой поверхности, при достаточной интенсивности, определяет то, что наиболее заметный перенос вещества будет вблизи нее, хотя максимум амплитуды вариации плотности приходится на пучность стоячей волны. Дело в том, что изменение плотности в данном случае имеет меньшее значение, чем ее градиенты. И как раз вблизи узловой поверхности, по разные ее стороны, знаки амплитуды всегда противоположны, определяя тем самым возможность диссипации энергии колебаний именно здесь. Через достаточно продолжительное время свойства узловой поверхности приобретут характер пограничной области между «ядром» и наружной частью тела. Возбуждение более высоких мод определяет наличие большого числа узловых поверхностей, «концентрация» которых не монотонна.

Эволюция вещества вблизи узловых поверхностей приводит к образованию отличающихся своими свойствами оболочек с более-менее четко выраженными границами. Рассмотренное идеализированное гомогенное тело в общих чертах соответствует общепринятым представлениям о внутреннем устройстве планет, хотя положение границ оболочек является несколько иным. Более того, «приближение упругого тела» не вполне корректно, и в связи с тем, что наличие вязкого трения приводит к достаточно существенному ангармонизму стационарных колебаний, а следовательно, и к тому, что положение узловых поверхностей будет несколько отличаться от приведенного на рис. 5.1.4. Еще одно обстоятельство некорректности модели стационарных состояний, характерное и для квантовой механики, связано с тем, что наличие возбужденных гармоник переводит систему в нестационарное состояние. Действительно, уже две стоячие волны в среде со скоростью распространения колебаний образуют бегущую волну со скоростью V < Vp, создавая условия для переноса и дифференциации вещества. Так, при наличии первой и второй возбужденных гармоник существует волна со скоростью вдвое меньшей, чем исходные (рис. 5.1.5). При наличии условий для ее переотражения возникает новая система стационарных состояний с гораздо большим периодом вариации плотности, хотя положенР1я ее узловых поверхностей будут совпадать с исходными.

Приведенное рассмотрение вскрывает в общих чертах механизм образования внутренних оболочек небесных тел, но исчерпывающим оно быть, конечно, не может. Дело в том, что приближение радиальных колебаний, по существу, одномерно и не охватывает существенных деталей явления. Сами радиальные колебания могут быть описаны совокупностью (в принципе, бесконечной) декартовых ортогональных компонент. В плоском (двумерном) варианте для центральной области резонатора, вьщеляя из всей совокупности ортогональную пару осей, имеем два взаимно перпендикулярных колебания, сложение которых приводит к образованию фигуры Лиссажу в форме круга, эллипса или прямой, в зависимости от начальной разности фаз суммируемых колебаний (рис. 5.1.6).

Подчеркнем еще раз, что независимое рассмотрение тангенциальных и радиальных колебаний некорректно для оболочек конечной толщины. В физике атома эта проблема была снята введением дополнительных спиновых мод колебаний. Фактически это означает то, что плоский топологический контур, связанный с движением электрона, не может быть синхронизован сам собой по причине иррационального соотношенрм радиального и тангенциального пути распространения сигнала, поскольку длина плоского контура зависит от

его диаметра иррациональным образом: L = Tid. Синхронизация возможна для слегка изогнутого контура в форме круга, начавшего сворачиваться в «восьмерку». Эта «изогнутость» как раз и описывается спиновыми модами, соответствуя на самом деле геодезической линии экваториального тора.

Структура и морфология планетарных оболочек формируются под действием как продольных, так и поперечных колебаний, причем границы оболочки превращают ее в «тонкий» сферический волновод. И если для тонкого плоского волновода самыми низкочастотными колебаниями являются моды с длиной волны порядка толщины волновода, то для цилиндрических и сферических волноводов с «сердечником» такого ограничения нет, поскольку компонента колебаний, ортогональная «замыкающейся» на стенках, имеет возможность замкнуться сама на себя, обогнув «сердечник» волновода.

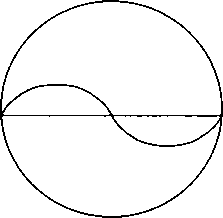
Рис. 5.1.2. Колебания второй моды

Третья гармоника имеет в качестве узла сферическую поверхность с радиусом Гуз = / 6.

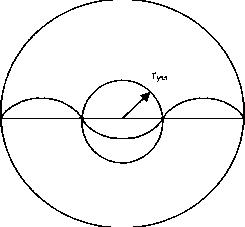
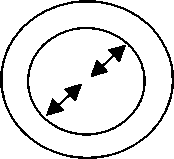
пример, термомеханические шумы. Они же могут возбуждать и более высокочастотные моды.

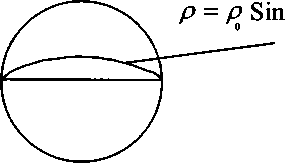
Рис. 5.1.1. Волновой фронт продольных колебаний и вариация плотности вдоль диаметра под воздействием основной моды

Вторая (кратная) мода продольных колебаний имеет узел в центре тела, а максимум вариаций плотности под ее воздействием приходится на половину радиуса.

Рис. 5.1.3. Колебания третьей моды

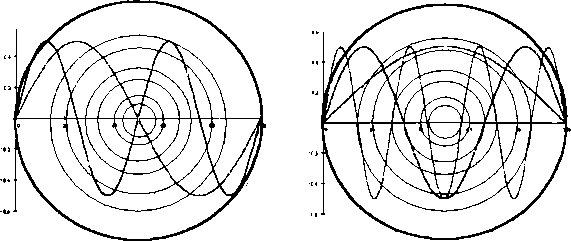
о 1/91/7 1/5 1/3 3/7 5/9 3/5 5/7 7/9 R

Рис. 5.1.4. Распределение узловых поверхностей вдоль радиуса тела

	щтт ^ ^ JT
* *^* — . ^
^ ‘ ^ •				•’-■”Г,”-. \
		“‘ – – ‘

Рис. 5.1.5. Образование бегущей волны в резонаторе с несколькими возбужденными модами

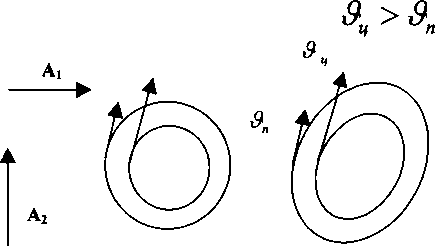
Рис. 5.1.6. Простейшие движения при сложении двух ортогональных колебаний А,,

Добавление всей остальной совокупности ортогональных разложений принципиальных особенностей не вносит. Вместе с тем такое движение для сплощной среды не реализуемо, поскольку скорости движения имеют максимум в центре резонатора, что для абсолютно жесткой среды приводит к верности результатов приближения радиальных колебаний. Среда, облада-

/

ющая некоторой вязкостью, испытывает значительно более сложное движение, понять которое можно лишь в трехмерной модели, где наличие отрицательного градиента угловых скоростей соответствует движению малых объемов по поверхностям тора. То есть вблизи центра тора скорости максимальны, а на периферии — минимальны, подобно структуре смерча. Интенсивное движение здесь, вероятно, приводит к образованию разрывов и расчленению оболочек. Видимо, подобными же явлениями объясняется образование планет из протопланетного облака с последующей локализацией рыхлых оболочек в компактные небесные тела. «Разрывы» плотных планетарных оболочек, вероятно, обладают большой скоростью релаксации и определяют структуру и отчасти морфологию планеты. Тороидальная структура характерна для всех оболочек, что приводит к существенной неоднородности внутри самой оболочки, разделяющейся на «струи» и «рукава». Но если образование межоболочечных разрывов и границ можно понять из анализа радиальных колебаний, то структуру самих оболочек легче исследовать в приближении тангенциальных мод.

КЛИМАТ

В рассмотрении минерагенеза в связи с факторами глобального масштаба приходится неизбежно сталкиваться с наличием климатических условий и, как указывалось выше, с наличием внешних магнитных и электрических полей. Ниже анализируются природа главного геомагнитного поля и обусловленные его вариациями климатические особенности.

Существует несколько гипотез относительно происхождения магнитного поля Земли и других планет. Так или иначе, они все опираются на некий внутренний источник. Наиболее распространенными являются гипотезы «намагниченного железного ядра» и «внутренней “динамо-машины”». Свойства железа в условиях центра планеты трудно вообразить или косвенно оценить, поэтому серьезно воспринимать гипотезу намагниченного ядра не приходится. Тем более что известно, что в условиях высоких температур железо не обладает магнитными свойствами и ядро для этой гипотезы должно быть достаточно холодным. Вторая гипотеза необходимо связана с колоссальными потоками электропроводящего вещества. В принципе, это вполне вероятно в условиях расплавленных пород, но условие возбуждения такой «динамо-машины» весьма проблематично.

Существует ряд оценок свойств магнитосферы (в частности, векторный характер полей), которые указывают на поверхностный источник поля, в качестве которого рассматриваются токи через земную кору. Сомнения в наличии внутреннего источника магнитного поля планеты подкрепляются и рядом других соображений. В частности, наличие у планеты атмосферы приводит к тому, что воздействие космического и солнечного ионизирующих излучений сопровождается образованием ионизированных электропроводящих слоев, которые в совокупности с электропроводной земной корой образуют две «обкладки» атмосферного (сферического) конденсатора. Емкость такого конденсатора нетрудно подсчитать из геометрии планеты. Заряд атмосферного конденсатора достаточно велик — его энергия сопоставима с энергией магнитосферы. Напряженность электрического поля внутри конденсатора (между обкладками) имеет радиальное направление, ее значение хорошо известно (порядка 100 – 200 В/м). Само по себе это на первый взгляд никакого отношения к магнитосфере не имеет. Однако помимо емкостных свойств обкладки конденсатора образуют сферический волновод, в котором могут распространяться электромагнитные колебания вполне определенной длины волны. В частности, волны короче двух метров свободно проходят через ионосферу, которая для них отражающими свойствами не обладает. Волны вдвое длиннее расстояния от поверхности до нижней границы ионосферы в атмосферном волноводе не распространяются (затухают). Все колебания с длинами волн от 2 м до 100 км «замкнуты» внутри ионосферного волновода, и их энергрм постепенно переходит к наиболее длинным волнам. Но длина волны в 100 км не является самой длинной для такого волновода, поскольку он имеет сферическую форму. Как только длина волны становрггся сопоставимой с длиной окружности планеты, магнитная ее компонента получает возможность замыкаться вокруг планеты, и волновод оказывается «прозрачным» для длин волн порядка 40 000 км. Точно так же волны метрового диапазона (телевизионные) внутри волновода сантиметрового диаметра (типичный размер антенного кабеля) распространяться не могут. Однако антенный кабель устроен несколько хитрее — имеет центральную внутреннюю жилу, вокруг которой магнитное поле метровых волн имеет возможность замыкаться, и кабель становится пригодным для передачи электромагнитных колебаний телевизионного диапазона.

Далее, сферическая геометрия атмосферного конденсатора приводит к тому, что он помимо емкости обладает и вполне определенной индуктивностью, которая рассчитывается, как и емкость, из геометрии планеты. Одновременное наличие емкости и индуктивности делает систему подобной колебательному контуру с собственной резонансной частотой около 2 Гц. В то же время верхняя граница низкочастотного диапазона «прозрачности» для длин волн в 40 000 км составляет 7,5 Гц. То есть в частотном смысле это достаточно узкий интервал. Однако колебания столь низких частот слабо затухают, поскольку им не на чем рассеиваться в атмосфере, и энергия этих колебаний сохраняется и, более того, пополняется за счет высокочастотного диапазона «прозрачности». Магнитная компонента электромагнитных колебаний имеет меридиальное направление и в совокупности с известной электрической радиальной компонентой соответствует основному электромагнитному полю Земли. Сопоставляя энергию атмосферного конденсатора с известной энергией магнитного поля планеты, следует сделать вывод о том, что природа магнитного поля почти целиком определяется наличием атмосферы. Подтверждениями этому выводу служат: отсутствие магнитосферы у небесных тел без атмосферы (Луна), слабость магнитосферы Марса, обладающего разреженной атмосферой, и, напротив, мощные магнитосферы планет, имеющих плотную атмосферу (Венера, Юпитер).

Казалось бы, электромагнитные колебания (какими бы низкочастотными они ни были) не могут иметь стационарных электрических и магнитных компонент. На самом деле эти волны распространяются не в однородной изотропной среде, а в сферическом волноводе. Поэтому для таких колебаний теряется зависимость от координат и времени, аналогично тому, как это происходит при интерференции колебаний с образованием фигур Лиссажу. Таким образом, магнитное поле Земли не существует само по себе, а является лищь компонентой электромагнитного и в этом смысле подобно веще

ственной элементарной частице, аналогичной известным объектам микромира.

Магнитное поле, будучи порождением атмосферного волноводного конденсатора, самым непосредственным образом влияет на характеристики атмосферы, в частности, на климат Земли и естественную структуру самой атмосферы (которая до сих пор серьезно не исследуется). Электромагнитное поле планеты помимо электрических и магнитных свойств обладает и вполне определенным механическим импульсом, направленным (как ему и положено) перпендикулярно двум другим компонентам поля. Таким образом, электрическая компонента направлена радиально, магнитная — меридиально, а механическая — по широте. Электромагнитное поле Земли может непосредственно влиять на движение слабо ионизированных воздушных масс вблизи поверхности, вплоть до инициации этого движения. Кроме того, атмосфера планеты представлена более чем на пятую часть кислородом, который является одним из сильнейших парамагнетиков. Это свойство обеспечивает сильный термодинамический эффект при изменении намагниченности парамагнетика. В частности, при размагничивании последний сильно снижает свою температуру. За счет этого вариации напряженности магнитного поля планеты приводят к температурным эффектам «похолодания» атмосферы. Наиболее известным примером такого влияния магнитосферы на климат являются утренние холода и даже заморозки. Они связаны с тем, что на восходе Солнца напряженность магнитного поля Земли снижается за счет изменения степени ионизации атмосферы и локального изменения параметров ионосферного конденсатора вследствие приливных эффектов.

Наложение на низкочастотные колебания высокочастотных приводит к возникновению интерференционных (муаровых) узоров, которые образзчот стоячие волны, приводя к пространственной модуляции магнитного поля. В тех участках поля, где напряженность снижается, происходит понижение температуры атмосферы, сопровождающееся измененрыми фазового состояния атмосферной влаги. Образуется либо туман, либо взвесь кристалликов льда, проявляющиеся в виде облаков, которые имеют вполне определенную интерференционную структуру. Это касается не только выразительно структурированных перистых облаков, но и длинноволновых порядков в расположении кучевых облаков. Последние с поверхности Земли наблюдать не всегда возможно, но они хорошо видны с борта самолета.

Длинноволновые структуры в распределении напряженности электромагнитного поля Земли имеют стационарную природу ввиду того, что самые низкочастотные резонансные колебания (2 Гц) замыкаются вокруг планеты в форме нескольких петель — пространственной фигуры Лиссажу. Возможно, что области «точек» самопересечения обладают аномальными свойствами. Возбуждения в верхней части низкочастотного диапазона вблизи 7,5 Гц приводят к модуляции поля со структурами порядка тысяч километров, для которых, так же как и для облачных структур, характерно изменение термодинамических параметров атмосферы. Детальный анализ структуры модулированных полей показывает, что они образованы из многих частных однонаправленных контуров (вращение в одну сторону) механической составляющей, которые вкупе с термодинамическими эффектами обусловливают образование циклонов.

На возбуждение верхней границы низкочастотного диапазона «прозрачности» ионосферного волновода оказывают влияние электрические процессы в литосфере, поскольку непосредственной взаимосвязи между низко- и высокочастотными диапазонами нет. Энергия высокочастотного диапазона, переходя от высоких частот к низким (волны с длиной порядка 100 км), рассеиваются на элементах земной коры того же размерного порядка. Происходит упругое и электромагнитное «раскачивание» коры, которое сопровождается сейсмическими колебаниями и сбросами, а также возбуждением низкочастотных электромагнитных колебаний в диапазоне ионосферного резонанса. На эти процессы естественным образом влияют особенности структуры и электрофизические свойства земной коры, а также явления массо- и зарядопереноса в литосфере, связанные с процессами минерагенеза.

Таким образом, магнитное поле Земли является компонентой электромагнитного и имеет атмосферную природу. Связь вариаций напряженности магнитного поля с климатом обусловлена парамагнитными свойствами атмосферы. Динамические структуры электромагнитного поля планеты проявляются в виде рисунков облаков, облачных масс, ветров, циклонов, смерчей и т. п.

Температура атмосферы является одним из основных параметров, определяющих климат. В свою очередь, основным фактором, определяющим температуру атмосферы, является поток лучистой энергии Солнца, прогревающий как саму атмосферу, так и подстилающую поверхность. Суточные и сезонные вариации этого потока формируют условия для вертикального и горизонтального тепломассопереноса, т. е. конвекции, адвекции и ветровых явлений. Скорости движения воздушных масс, а соответственно, и переноса тепла при этом составляют 1^2 % от скорости звука, достигая при ураганах 10 %. Помимо переноса тепла с указанными скоростями существуют механизмы теплопередачи в атмосфере со скоростями звукового и светового диапазонов. Последнее, например, тривиально реализуется за счет радиационного обмена.

Другой механизм вариаций температуры атмосферы может реализовываться за счет магнитных свойств воздуха и материалов (минералов, пород, природных растворов) подстилающей поверхности. Вариации напряженности магнитного поля за счет процессов в ионосфере, например, могут вызывать разогрев осадочных и обводненных бассейнов, среда которых обладает достаточной электропроводностью, а также ферромагнитных сред в районах магнитных аномалий. Эти явления, безусловно, влияют на температуру атмосферы, но они так же инерционны, как и традиционно рассматриваемый тепломассоперенос.

Вариации напряженности магнитного поля могут оказывать и непосредственное влрмние на температуру воздуха благодаря наличию у последнего значительных парамагнитных свойств, обусловленных в основном наличием кислорода. Удельная магнитная восприимчивость газообразного кислорода составляет величину 1320 X 10 ’ мУкг. Азот—основной компонент атмосферного воздуха — является диамагнетиком с отрицательной величиной удельной магнитной восприимчивости (-5,3 X 10’ mVkt). Результирующая восприимчивость

Не вдаваясь в детали анализа, рассмотрим изменение температуры парамагнетика при адиабатическом )^ень- шении напряженности магнитного поля, т. е. в таком процессе, когда не происходит теплообмена и можно считать энтропию S среды неизменной. В этом случае

В свою очередь, намагниченность идеального парамагнетика зависит только от отношения напряженности Н и температуры среды Т, т. е.

В предшествующем размагничиванию изотермическом процессе внутренняя энергия не меняется и теплота

Если выполняется закон Кюри, т. е. функция f линейна, то

Из опыта известно, что зависимость внутренней энергии парамагнетика от температуры имеет вид:

Следовательно, изменение удельной энтропии в изотермическом процессе:

S = (4/3) X ar-C(H/T)2/2 + const. Поскольку при адиабатическом уменьшении напряженности от Hj до изменения энтропии не происходит, то можно записать:

(4 / 3) X а (Т,^ – Т/) = С ((Н, / – (Н,/ Т,)^) / 2.

Это выражение показывает возможность значительного охлаждения атмосферного воздуха, например, при быстрой инверсии магнитного поля Земли. В этом случае, поскольку парамагнетизм присущ кислороду как в газообразном, так и в жидком состоянии, охлаждение может продолжаться вплоть до его вымораживания, т. е. понижение температуры атмосферы может составить почти две сотни градусов. Причем такое похолодание интенсивно развивается в областях с уже низкой температурой, поскольку исходная температура стоит в знаменателе.

Инверсии магнитного поля Земли хотя и являются историческим фактом, но в реальном масштабе времени события достаточно экзотические. Небольшие вариации магнитного поля обыденны и составляют в приземном слое единицы, достигая иногда десятка процентов. Оценка связанных с этими вариациями изменений температуры воздуха дает величины до нескольких градусов.

Причины вариации магнитного поля Земли могут иметь эндогенную и экзогенную природу. Полагая вариации эндогенной природы инерционными, за исключением, может быть, катастрофических явлений, можно считать, что их вклад в адиабатические процессы отсутствует. Экзогенные вариации связаны в основном, так или иначе, с ионосферными явлениями, хотя прямой связи с возмущениями магнитного поля в верхних и приземных слоях атмосферы, как правило, не наблюдается.

Ионосфера представляет собой электронейтральную плазму, для которой характерно наличие собственных резонансных частот:

воздуха имеет положительное значение, характерное для парамагнетика с величиной 270 х 10 ^ м^/кг. Классические термодинамика и электродинамика предсказывают эффект понижения температуры парамагнетика при адиабатическом размагничивании. Это явление иногда используется в технике низких температур как эффективный способ охлаждения.

dS = 0

для идеального парамагнетика внутренняя энергия среды и не зависит от напряженности магнитного поля Н:

dU = TdS + HdM,

здесь Т — температура среды;

Н — напряженность магнитного поля;

М — намагниченность среды.

M = f(H/T) = xH,

где X = С / Т соответствует закону Кюри.

dQ = – HdM,

Hi

откуда

Q=-C/T, jHdH=-(C/2Ti)x(Hf -Н^),

здесь Т, — температура изотермического процесса.

и = аТ\

где а > 0.

dS = (1 / Т) X (dU – HdM) = 4аТМТ – (С (Н / T)d (Н / Т)) и

S, = (4 / 3) X аТ,з – С (Hj / Т,)2 / 2 + const,

= (4 / 3) X аТ/ – С (Н^/ / 2 + const,

И т к S — *

Если = о, т. е. поле исчезает полностью, а мало, то Т,-Тз = (СН,2)/(8аТ/)

соответствует понижению температуры парамагнитной среды при адиабатическом размагничивании от до Т^, где Т, > Т^, так как в последнем выражении С > 0 и а > 0.

1. ^ = 4тте^ / т,

   где п — концентрация зарядов;

   е — элементарный заряд;

   m—масса носителя заряда (масса иона или электрона).

   Спектр ионосферных резонансов, в соответствии с уравнением, содержит ионную и электронную полосы вследствие различия масс ионов и электронов. Характерные частоты электронной компоненты резонансов

   имеют величину в дневное время 1СИ-30 МГц, в зависимости от концентрации электронов, которая составляет 10^-^ 10’ электронов в кубическом сантиметре. Несмотря на столь малую концентрацию, общее количество частиц в ионосфере достаточно велико и составляет величину N = 10^^. Энергию ионосферы, связанную с колеба

   ниями на частоте можно оценить как сумму энергий элементарных «диполей», участвующих в резонансе:

   Величина амплитуды А диполя, в свою очередь, может быть оценена по радиусу дебаевского экранирования А ~ г . Для ионосферы г ~ 10’^м. Отсюда получаем

   Напряженность магнитного поля Земли Н у поверхности в среднем составляет величину примерно 30 А/м. Плотность энергии

   = 2л X 10’ X ff ~ 2 X 10-3 Дж/м\ а энергия щарового слоя толщиной 1 метр W =4яЯ’х 1 XW ~6х 10′”х2х 10-3 = 12 X Ю» Дж.

   Порядок величины энергии резонансных частот ионосферы 8р близок к энергии магнитного поля в приземном слое атмосферы. В то же время наличие радиочастотных резонансов в верхних слоях атмосферы никоим образом не связано с вариацией постоянного магнитного поля в нижних слоях. Такая связь могла бы обнаружиться при наличии инфранизких частот поля, генерируемых ионосферой. Такая возможность существует, поскольку в выражении для частоты фигурирует концентрация зарядов ионосферной плазмы. Концен- трацр1я зависит от процессов ионизации под действием коротковолновой радиации Солнца и космического излучения, с одной стороны, и конкурирующего процесса рекомбинации зарядов с образованием нейтральных атомов — с другой. Вследствие этого концентрация и, соответственно, резонансная частота имеют суточные вариации. Отсюда немедленно следует тривиальный вывод, что самая низкочастотная компонента в суточном спектре резонансных частот ионосферы имеет период 24 часа. Если существует резонансная система с таким периодом колебаний, то вполне вероятно ее возбуждение с последующей релаксацией, в том числе и импульсного характера при достижении критических параметров. Такая система, однако, должна иметь космические размеры и существенным образом зависеть от состояния ближнего космоса, включая распределения планетных масс и полей околосолнечного пространства. Вьщелить столь масштабные накопители энергии электромагнитного поля достаточно сложно, поэтому перейдем к анализу резонансной системы планетарного размера, а именно к слою атмосферы, простирающемуся от поверхности Земли до ионосферы. Этот слой ограничен с обеих сторон поверхностями с ненулевой электропроводностью. Для частот электромагнитного поля ниже частоты резонанса ионосферы обе поверхности являются хорошими отражателями.

   Нижние слои атмосферы представляют собой практически идеальный волновод сферической конфигурации для частот ниже частоты резонанса ионосферы. Исключение составляют лишь электромагнитные колебания с частотами, соответствующими ионному резонансу ионосферы порядка 100 кГц. Со стороны нижних частот также существует ограничение, связанное с собственной частотой резонанса волновода ввиду его геометрической замкнутости. Действительно, емкость конденсатора, образованного поверхностью Земли и нижней поверхностью ионосферы, может быть оценена как

   С = S / (4яЬ),

   где S — поверхность Земли;

   h—расстояние от поверхности Земли до ионосферы. Индуктивность шарового слоя зависит только от его толщины:

   L = (4лЬ) / с^.

   Резонансная частота может быть определена как

   Здесь R ~ 6,5 X 10* метров (радиус Земли), а с ~ 3 х Ю* м/с (скорость света).

   Соответствующая длина волны электромагнитного колебания составляет

   = с / V = (3 X 10«) / 2,07 ~ 1,5 X 10* м. Естественно, что волна такой протяженности не может дать простого контура замыкания, поскольку окружность Земли имеет величину 4 х Ю’ м. Устойчивая конфигурация, соответствующая резонансу с образованием стоячей волны, образуется при многопетлевом «замыкании» в кваркоподобную структуру. Структура электромагнитного поля низшей недиссипирующей моды Земли составляет предмет специального исследования, выходящего за рамки данной работы. Отметим здесь лишь то, что при многопетлевом «замыкании» электромагнитной волны на поверхности геоида поле с ненулевой частотой образует стационарную структуру. Это кажется на первый взгляд парадоксальным, но магнитное поле Земли имеет чисто электромагнитную природу, соответствуя низшей моде резонанса в волноводе, образованном поверхностями планеты и ее ионосферы. Оценим энергию поля волноводного резонатора, на

   пример, по известной напряженности электростатического поля Земли, которая имеет вертикальную (основную) компоненту величиной порядка 200 В/м. Так как емкость волновода

   С = 8/4яЬ,

   энергия может быть определена как энергия конденсатора: W = (Си^) / 2,

   здесь и = Eh, где Е—напряженность поля (Е ~ 200 В/м), W = (R ^E^h) / 2.

   Считая h ~ 5 X 10″ метров, получаем W = ((6,5 X 10^)2 X (2 X 102)2 X 5х 10″) / 2 = 4 X 1022 Дж, что по порядку величины соответствует энергии магнитного поля Земли. Это является косвенным подтверждением высказанного выше предположения о динамической природе магнитосферы. Интересно еще раз отметрггь, что небесные тела, не имеющие атмосферы, как правило, лищены и магнитосферы.

   Спектр собственных частот сферического волновода, помимо резонансной и ее гармоник v = nv^, где п — целые числа, содержит также частоты, соответствующие проекции резонансных колебаний на «гладкий» контур. Длина последнего соответствует максимальной окружности геоида и имеет величину 2лК^ 4 х м. Замкнутой волне X, = 2nR^ соответствует частота v = с /X ~ (3 X 10*) / (4 X 10’) = 7,5 Гц. Примечательно то, что последняя частота имеет особое значение в спектре солнечного излучения, с одной стороны, и в физиологии человека — с другой, а отношение низших резонансных частот удовлетворяет «золотому сечению».

   Можно вообразить фантастическую ситуацию, когда все радиостанции и другие источники радиоизлучений отключены, а ионосфера очень спокойна и также не генерирует радиоволны. В таком случае все радиоволны в результате переотражений и рассеяния с той или иной скоростью релаксируют, отдав свою энергию низшей моде с частотой 2,07 Гц. При этом все же остается возможность низкочастотных вариаций поля вследствие того, что низшей моде соответствует полоса частот вполне определенной ширины. Длина «гладкого» контура вблизи поверхности Земли и вблизи ионосферы отличается на величину 2кЪ. Поэтому проекция основного колебания на «гладкий» контур также отличается на указанную величину.

   Соответствующие частоты можно определить как V = с / (27tR )

   и вследствие этого возникает резонансная частота д V = V – V ,

   Av ~ 5,6 X 10-^ Гц.

   Эта частота представляет собой биение с периодом Т = l/Av = 18 с в форме импульсов с продолжительностью порядка 5 X 10″^ с. Вариация постоянных составляющих поля при этом может быть как с возрастанием напряженности, так и с убыванием. В последнем случае реализуется ситуация адиабатического размагничивания в виде волны понижения температуры воздуха, обегающей земной шар со скоростью радиоволны. Наличие таких скачкообразных похолоданий на доли градуса при совершенно спокойной атмосфере может ощутить любой внимательный наблюдатель без всякой аппаратуры.

   Помимо рассмотренного механизма вариаций напряженности магнитного поля существует целый ряд

   других, причины которых связаны со значительным непостоянством параметров сферического волноводного слоя. Изменения емкости происходят вследствие, например, приливных явлений, которые в большей степени деформируют атмосферу, чем гидросферу и подстилающую поверхность. Локальное изменение емкости сопровождается локальной же перестройкой спектра собственных частот. Это порождает релаксационные импульсы с периодом следования продолжительностью полсуток, сутки и так далее.

   В общем случае приливные явления и процессы изменения концентрации ионосферной плазмы под действием солнечного и космического излучений приводят к тому, что в той или иной мере возбуждены многие, если не все, моды собственных колебаний поля в сферическом волноводе. Следует также отметить, что кроме тангенциальных мод, рассмотренных выше, существуют и нормальные для волн, распространяющихся в вертикальном направлении. Время жизни этих колебаний за счет инверсии в тангенциальные невелико, но в результате нестационарности ионосферы они возбуждены практически всегда. Длина волны низшей нормальной моды определяется величиной h:

   \ = 2h,

   что соответствует частотам порядка

   V = с/\ = (3 X 10») /10^ = 3000 Гц.

   Этой моде при h = 50 км должна соответствовать пучность (максимум изменения напряженности поля) на высоте 25 км. Пучности высших гармоник нормальных колебаний будут наблюдаться на высотах h/n, где п = 3.., т. е. примерно 17; 12,5; 10; 8,7 км и на более низких высотах. Причем вследствие большой вероятности релаксации нормальных колебаний в тангенциальные может оказаться, что заселенность высших мод будет выше нижних.

   Заселенность (возбужденность) спектров нормальных и тангенциальных колебаний поля приземного волновода, т. е. наличие в нем стоячих волн гармонически связанных частот, приводит к появлению бегущих волн в общем случае несинусоидальной формы и со скоростями распространения значительно меньшими скорости света. Это достаточно общий вывод из теории колебаний. Более того, и эти комбинационные волны могут образовывать свои стоячие волны весьма большой протяженности. На фронте бегущих несинусоидальных волн вполне реализуются условия для адиабатического размагничивания со значительным понижением температуры.

   Помимо рассмотренного механизма связи вариаций электромагнитного поля в приземном слое с термодинамическими параметрами атмосферы существуют и другие возможности. Например, возникновение магнитогидродинамических, в том числе звуковых, колебаний инфранизких частот и другие, такие как непосредственное изменение плотности и давления под действием низкочастотных компонент вектора Пойнтинга: Р = Н х Е.

   Оценка механической компоненты электромагнитного поля приземного слоя по его «статическим» напряженностям позволяет предположить наличие вариаций давления в пределах первых процентов от атмосферного. В любом случае термодинамические параметры атмосферы связаны уравнением состояния:

   Р = КрТ,

   где Р — давление; р — плотность; Т — температура; К — константа.

   Изменение любого из параметров приводит к появлению релаксационного процесса волнового характера с наличием как бегущих, так и стоячих волн давления, плотности и температуры.

   Таким образом, приземный слой атмосферы структурируется интерференционными картинами первичного порядка, т. е. интерференцией магнитных полей, и вторичного — интерференцией звуковых волн ин- франизких частот. Помимо аппаратурных методов регистрации вариаций параметров электромагнитного поля и термодинамических потенциалов природа предоставила возможность визуального наблюдения интерференции в атмосфере. Существенный ее компонент — пары воды — склонен к фазовым переходам в реальных диапазонах вариаций термодинамических параметров. Поэтому интерференционные «пятна» с пониженной температурой или повыщенной плотностью «декорируются» каплями воды или кристаллами льда. Изменение фазовых состояний в электромагнитных и звуковых полях приводит к изменению формы облаков, создает видимость их движения в отсутствие реальных воздушных потоков, контролирует их образование и исчезновение. Более того, подвижность атмосферы, т. е. наличие ветров, есть не что иное, как результат образования бегущих волн из низкочастотных стоячих. Скорости этих в общем случае несинусоидальных волн значительно ниже скорости звука.

   Приведенное изложение позволяет в грубом приближении рассмотреть каскад волновых процессов, ответственных за тепломассоперенос в атмосфере и не связанных непосредственно с традиционно рассматриваемыми явлениями конвекции, адвекции и ветро- вой подвижностью. Здесь имеется в виду слабая общая изученность вопроса в отношении взаимодействия магнитного поля и движущихся сред, для которого характерно невообразимо большое число типов колебаний с соответствующими частотами и скоростями переноса.

   Волновые процессы в общем балансе тепломассо- переноса составляют, вероятно, значительную, если не доминирующую, долю. Действительно, образование циклонов и антициклонов связано, видимо, целиком именно с волновыми процессами, а их перемещения — не с потоками воздушных масс глобального характера, а с изменением фазовой картины низкочастотных электромагнитных и инфразвуковых полей. Причем во всей области циклона термодинамику процесса, скорее всего, контролирует именно волновой процесс, а не сторонние источники тепла. Учитывая упоминавшийся выше многопетлевой кваркоподобный характер замыкания низкочастотных колебаний на поверхности геоида, можно утверждать, что если существует один циклон, то одновременно существует еще несколько циклонов и антициклонов. Это является следствием того, что замыкание колебаний образует на поверхности геоида несколько контуров и узлов самопересечения.

   Более полное выявление природы тепломассопере- носа в атмосфере, безусловно, необходимо для практических целей прогноза погоды и оценки влияния на нее антропогенной деятельности. В то же время наблюдение неслучайных конфигураций облачных масс представляет и просто эстетическое наслаждение.

   Наиболее интересны распределения облаков во время изменения лунных фаз, когда совпадают приливные явления, вызванные Солнцем и Луной. Интересны также интерференционные картины, декорированные облаками, на восходе и закате Солнца, связанные с изменением концентрации ионосферной плазмы. С последним связаны и известные всем утренние «заморозки», когда Солнце «выкатывается» из-за горизонта.

   «Статическая» конфигурация магнитосферы, помимо характерной для правильного сферического волновода, в значительной мере определяется и локальными особенностями рельефа земной коры, а также распределением магнитных масс типа железорудных месторождений. Первое является следствием того, что элементы земной коры имеют значительный перепад высот, достигающий величин порядка десяти и более процентов от расстояния между ионосферой и подстилающей поверхностью. Соответственно этому, локальная емкость ионосферного конденсатора сильно зависргг от рельефа, определяя, в свою очередь, плотность энергии низшей моды ионосферного волновода. Следует отметить, что вариацрш плотности энергии, связанные с рельефом, не вносят существенных искажений в низкочастотную часть спектра магнитосферы, поскольку в первом приближении она не зависит от толщины слоя.

   Действительно, v ~ 1 / (LC)‘^^, но зависимость L от h прямо пропорциональна, а С имеет обратную зависимость. В то же время спектр радиальных мод непосредственно связан с расстоянием между ионосферой и подстилающей поверхностью. Поэтому в районах высокогорья комбинационный спектр магнитосферы значительно отличается от равнинного и океаническо

   го. Проявлением такого отличия, вероятно, является долгоживущий антициклон Монгольского плоскогорья.

   Зависимость конфигурации магнитосферы от распределения магнитных масс является известным обстоятельством и наблюдается в виде магнитных аномалий. Mexaiffl3M влияния магнитных аномалий на температуру и, соответственно, на всю термодинамику атмосферы заключается в том, что за счет гистерезиса происходит сглаживание фронтальных областей магнитных вариаций. Вследствие этого смягчается и эффект адиабатического размагничивания, то есть размах понижения температуры в областях магнитных аномалий несколько ниже, чем в других регионах. Интегральная, среднегодовая, например, температура в районах магнитных аномалий должна быть, следовательно, несколько вьпие средней по всему региону.

   С}ггочные вариации магнитосферы и связанные с этим изменения температуры, как отмечалось выше, связаны с изменением концентрации ионосферной плазмы и приливами. Этими же обстоятельствами определяются и сезонные вариации, поскольку с изменением наклона земной оси происходит смещение как области максимальной инсоляции, так и приливной зоны.

   Следует подчеркнуть, что вариации напряженности магнитосферы имеют характер временных и пространственных биений, возникающих при возбуждении второй и последующих мод ее колебаний, в то время как напряженность основной моды имеет достаточно стационарный характер. Время жизни основной моды можно примерно оценить, зная добротность ионосферного волновода, через величину полуширины ее частотного диапазона из феноменологического соотношения (эквивалентного принципу неопределенности):

   ДуДт > 1.

   Полагая, что добротность определяется в основном диссипацией энергии поля, вызываемой быстро движущимися частицами, мы можем пренебречь нестаци- онарностью ионосферы, вариациями других параметров столь сложной системы и учесть только влияние электронов вещества подстилающей поверхности, где их концентрация наиболее высока, достигая величины порядка 10^^-^-10^^ в кубическом сантиметре. Соответствующая резонансная частота в этом случае составляет около 10’® Гц. Можно считать, что участие электронов во взаимодействии с магнитным полем, с одной стороны, и механическим импульсом планеты — с другой — выражается в том, что «укорачивается» период колебаний основной моды на = 1 / v^, то есть на величину порядка 10‘® с, следовательно, полущирина Ду = 1 /Т-1 / (Т-т)~т /T^ = vVv,

   откуда

   Дх = 1 / Ду ~ 10‘® с.

   Эта величина несколько превышает известную из палеомагнитных данных 10’^^ 10’^ с, что свидетельствует о грубости рассматриваемой модели, не учитывающей другие каналы диссипации и некоторые существенные детали как ионосферы, так и магнитосферы. К существенным деталям такого рода относится неоднородность ионосферы в вертикальном направлении, которая проявляется в наличии нескольких слоев. То есть помимо приземного волновода существует, по крайней мере, еще один стационарный, на высоте примерно 100-^190 км. Это связано с тем, что максимум ионизационной способности ультрафиолетового излучения реализуется на высотах порядка 200 км. Более жесткие рентгеновские излучения производят иониза- цию наиболее эффективно в конце многоэтапного рассеяния на высотах 50^100 км. Поскольку резонансная частота сферического волновода не зависит от толщины слоя, то ее можно грубо оценить по высоте нижней границы, где

   R – R + 100 км.

   Отсюда (Vp = с / ((R^+ 100 [км]) х ~ 2,04 Гц) видно, что частоты обоих слоев близки, но эта близость связана с тем, что в напряженности поля присутствуют существенные биения на комбинационной частоте Av = Vp* – Vp^ ~ 0,03 Гц, т. е. с периодом порядка 30 с. Поскольку атмосфера — наиболее чувствительный элемент планеты по отношению к прршивным возмущениям, то следует полагать, что так же чувствительна к ним и высота второго волновода. Следовательно, вследствие приливных возмущений частота основной моды «медленно плывет», порождая длиннопериодические импульсные изменения магнитного поля планеты.

   В заключение следует отметить, что, несмотря на нетривиальную конфрпурацию магнитосферы приземного слоя, ее интегральная структура в значительной мере соответствует магнитному диполю и имеет два разре- шеьшых состояния с осью, почти совпадающей с осью механического вращенрм. Возмущегом магнрпного поля с моментами, не совпадающими с механическим моментом импульса, производят механическую работу в атмосфере и частично в гидросфере и в конечном итоге приводят к их разогреву. Дрейф магнитных полюсов и их отклонение от географических связаны с тем, что полный момент импульса планеты не совпадает с его собственной осью вращения. Это определяется скорее не внутренними процесеами, а влиянием всех небесных тел. «Траектория» дрейфа магнитного полюса «отслеживает» суммарный момент импульса Космоса в области планеты. Конечно, наиболее существенно влияние соседних тел, проявляющееся в «спиральности траектории дрейфа». Но постоянная незамкнутость этой спрфали есть проявление влияния отдаленного Космоса.

   Рассмотренные выше механизмы климатических процессов не исчерпывают всю совокупность причин вариаций термодинамических параметров атмосферы. Не менее существенно на подвижность атмосферы влияние процессов в земной коре, связанных с сейсмическими колебаниями. Последние, помимо непосредственного вовлечения атмосферы в движение, активно взаимодействуют с колебаниями электромагнитного поля, усложняя тем самым описанную выше картину.

   Наличие магнитосферы планет непосредственным образом связано с атмосферой, в частности, с образованием сферического волноводного резонатора в слое между поверхностью планеты и ионизованной частью атмосферы. Магнитное поле планеты в основном соответствует магнитной компоненте 1шзшей моды электромагнитного поля ионосферного волноводного резонатора.

   Возмущения магнитного поля планеты являются следствием вариаций параметров ионосферного волновода под действием приливных сил и переменной интенсивности солнечного излучения.

   Интерференция низкочастотных гармоник электромагнитного поля, соответствуюпщх комбинационным частотам в спектре волноводного ионосферного резонатора, проявляется во влиянии на термодинамические параметры атмосферы и в значительной мере ответственна за механические (ветра), тепловые и фазовые (изменение плотности с конденсацией паров воды) эффекты в атмосфере, определяя тем самым климат планеты.

8 = S то) W / 2.

р р

8р~10М0″Дж.

Vp = (l/2)x(7t2LC)>’l

max З”

И

”шш = с/(2я (Кз + Ь)),

max mm’

ЛИТОСФЕРА

Каждый внутренний слой и кора планеты, будучи ограниченными с обеих сторон веществом с резко отличными дисперсионными свойствами, представляют собой волновод для тангенциальных сейсмических колебаний. Структура напряжений для низшей моды тангенциаль- ш>1х колебаний сферической оболочки во многом подобна структуре рассмотренного выше электромагнитного поля, если рассматривать колебания поперечного типа. Продольные волны, конечно же, осложняют общую картину. Тем не менее, наличие шести континентов и четырех океанов на нашей планете соответствует как раз кваркоподобной трехпетлевой самоинтерференции основной моды поперечных колебаний земной коры (рис. 5.3.1).

В узловых областях между ю)нтинентами вдет интенсивное преобразование энергии колебаний в тепло, что непосредственно проявляется в вулканических процессах.

Континентальные образования, будучи ограниченными узловыми областями, на которых скорости сейсмических волн испытывают значительный скачок, сами по себе являются резонаторами для более высокочастотных колебаний. Граница континента развивается не только за счет «первопричинных» колебаний земной коры, но и за счет собственных колебаний, для которых граница является основной узловой областью. Спектр континентальных мод осложнен геометрией континентов, очертания которых изначально являются «неправильными», поскольку контуры кваркоподобной первой модели вытянуты и ограничены «кусками» пересекающихся кривых линий. Тем не менее, комбинация первых и вторых континентальных мод образует свою узловую область, которая чаще всего декорируется руслами великих рек, проходящих обычно по тектоническому разлому.

Тектоническими разломами оконтуриваются региональные резонансные структуры, узловые области которых соответствуют развитию сетей локальных особенностей рельефа.

К этим локальным особенностям обычно приурочены процессы минералообразования гипергенного и эндогенного характера.

Казалось бы, редукция глобальных явлений к региональным противоречит известному физическому опыту. Действительно, существующая парадигма полагает, что энергия высокочастотных колебаний переходит в энергию низкочастотных, но не наоборот, как рассматрива-

Переход к колебаниям с меньшей амплитудой связан с импульсным сбросом энергии. Количество «сброшенной» энергии пропорционально разности квадратов

амплитуд до сброса и после сброса, а также массе коры и квадрату частоты основной моды.

Грубую оценку величины энергии сброса можно осуществить следующим образом:

Масса коры ni^ ~ 4TiR^^dj^p^, где радиус планеты

~ 6,5 X 10® м, толщина коры ~ ~ 5 х Ю’* м, плот

Частота основной моды со, ~ 2я / х, где х = А, / v, то есть при средней скорости поперечных волн \ ~1 х м/с и длине волны, с учетом рассмотренного выше трехпетлевого замыкания, А. ~ 3 х 2^R^ ~ 1,2 х Ю* м, X = 17 000 с ~ 5 ч. Отсюда со ~ 3,7 х рад/с. Полагая, наконец, амплитуду колебаний в пределах 10 * м, а соответственно, разность квадратов амплитуд порядка 10’^ м^, имеем вполне реалистичную оценку энергий землетрясений ~ 5,5 х Ю’^ Дж, даже несколько заниженную. Частоту основной моды можно определить и другим, более прямым, способом из свойств литосферы. Период упругих резонансных колебаний системы Тр ~ 2я (ш /

Зная модуль сдвига G ~ 4 х Ю’® Па, к ~ 2Gd,^. Отсюда Тр ~ 2я (2R^p,^ / G)‘’^ ~ 7,8 часа близко к использованному выще значению.

Оценку длительности сброса можно сделать на основе голографического соотношения AvAx > 1, если определить ширину полосы частот спектра колебаний земной коры. Последнее можно выполнить, формально перейдя от нелинейности в зависимости амплитуды от частоты к распределению амплитуд по частотам. Впрочем, значенрм амплитуд в данном случае и неважны.

Самая низкая частота нами уже определена. Наибольшую частоту можно оценить по длине стоячей волны в самых тонких участках коры.

Известно, что толщина коры колеблется от 15 км под океанами до 200 км под материками. Следовательно, X . = 2d ~ 3 X 10’* м, отсюда

V = V / X ~ (7 X 10^) / (3 X 10^) 2,3 X 10-* Гц.

Тогда «длительность» сброса Ат = 1 / ~ 1/

Грубую оценку повторяемости сбросов можно сделать следующим образом. Если предположить равномерность распределения мод колебаний по спектру, то их число N = / v^.^. Период биений между соседни

Т = т xN = v /V 2 = (2,3 X 10-*)/(3,6х 10-’) =

Из самых общих соображений можно оценить также и детали кинетики сброса. Поскольку длительность импульса составляет несколько секунд, то и сам сброс представляет собою серию импульсов с периодом того же порядка. Далее, биения прршивных и сейсмических волн проявляются в серии сбросов с периодом около 7 суток: можно наблюдать либо один сброс, либо два примерно равных по интенсивности через неделю, либо слабый и через неделю сильный, а еще через неделю снова слабый. «Неделя» здесь — условный период, основанный на грубой оценке.

Мониторинг фаз в спектре собственных колебаний коры, необходимый для прогноза землетрясений, представляется чрезвычайно сложным технически. Более того, необходим еще и учет астрологических конъюгаций. Вместе с тем совершено ясно, что наиболее активными зонами сбросов являются области узловых линий в конфигурации стоячей сейсмической волны. Именно здесь напряжения в соседних участках коры имеют противоположный знак, и, соответственно, здесь наиболее нарушены породы. Поэтому эти области управляют фазовыми соотношениями в спектре сейсмических колебаний, а поскольку в области разрыва происходит «сосредоточение» крайних узлов для верхних мод, то и сброс реализуется, как правило, здесь. Значительно реже должны наблюдаться сбросы на внутриконтинен- тальных резонансных конфигурациях.

Таким образом, на поверхности планеты должны наблюдаться линейные области высокой сейсмоактивности, причем эти линии совпадают с контурами трехпетлевой структуры низкочастотной моды.

Наличие высокочастотных составляющих в импульсе сброса энергии сейсмических колебаний коры определяет возбуждение региональных и локальных колебаний, служащих каналами диссипации энергии, снимающими напряжения, возникшие в результате низкочастотной накачки. Здесь необходимо заметить, что рассмотренный механизм образования и возбуждения высокочастотных структур имеет чрезвычайно общий характер. Интересно, что и долгоживущий протон за время своей жизни (ориентировочно 10^^ лет) в результате сбросов напряжений в своих основных модах развивает внутри себя целую иерархию структур под действием внешних условий, сохраняя при этом протонный облик. Образно говоря, в элементарной частице заключена вселенная, эквивалентная нашей, что соответствует утверждению Фридмана о том, что Вселенная извне выглядит как элементарная частица. Показано, что любая достигающая совершенства система обретает черты элементарной частицы, и этому состоянию присвоено название «фридмон». Таким образом, развитие систем может осуществляться не только по известному термодинамическому механизму (от высокочастотного к низкочастотному), но и в обратном направлении.

Рис. 5.3.1. Линия глобального линеамента

ЛОСЬ выше. На самом деле никакого противоречия нет. Для низкочастотной основной моды колебаний земной коры, как, впрочем, и для всех других, гармоническое приближение является достаточно грубым упрощением. Зависимость амплитуды от частоты в действительности имеет место, и, более того, она нелинейна. С другой стороны, размах амплитуды вряд ли выходит за рамки упругих взаимодействий вещества коры, и поэтому, в принципе, отсутствуют каналы диссипации энергии низкочастотных колебаний. Следовательно, низкочастотная мода обладает некоторой пороговой энергоемкостью. При достижении этого порога за счет энергии верхних мод, возбуждаемых за счет гравитационных (приливных) возмущений и энергии процессов в более глубоких слоях планеты, происходит скачкообразный переход к колебаниям с той же частотой, но с меньшей амплитудой. Такие переходы характерны для пилообразной кривой, описывающей нелинейные колебания.

Рис. 5.3.2. Зависимость амплитуды от частоты

ность коры ~ 3 X 10^ кг/м^, то есть ~ 8 х кг.

где m — масса литосферы, а к — ее жесткость.

й . =Х . 12.

mm min

(2,3 X 10-*) = 4,5 с.

ми модами Tg > 1 / тогда время, необходимое для совпадения фаз колебаний всех мод, составит

= 6,4 X 10= [с] = 180 [ч] = 7,4 [сут].

То есть период между сейсмосбросами, определяемый из геометрических параметров планеты, совпадает с периодом смены лунных фаз. Вряд ли это совпадение является случайным. Тем не менее, взаимодействие приливных и сейсмических волн ведет к интересным следствиям, которые выражаются в том, что реальный период между сбросами определяется не биениями собственных мод в спектре колебаний земной коры, а биениями между приливными и сейсмическими волнами. То есть сбросы с периодом 7,4 суток (это грубая оценка) подавляются приливными эффектами с периодом 7 суток. Соответствующий реальным сбросам период Tr = 1 / Vg = 1 / (1 / Tjj- 1 / Т^) = (Xj, X Xg.) /

(1^-1^,) = (7,4×7)/0,4 =130 [сут].

Величина сбрасываемой энергии определяется суммой «подавленных» сбросов: ^ ^ (Tr / = 17,5 х Е^,

это более чем на порядок превышает энергию собственного сброса. Мощность, развиваемая при сбросе, из приведенных выше оценок энергии и времени сброса составляет величину порядка 2 х Вт, что обеспечивает при локальном характере сброса условия для чрезвычайно активного, в том числе высокотемпературного, минерагенеза.

ВОДОРОД

Закономерная приуроченность месторождений различных типов к тем или иным мотивам регионального рельефа известна давно и столь же давно ждет своего объяснения. Хорошо известна связь минерагенеза с динамическими особенностями земной коры, например, вулканизмом или разрывно-сдвиговыми процессами. Объяснения здесь напрашиваются сами собой, поскольку в обоих случаях резко меняются термодинамические условия и интенсивность транспортных явлений, нарушающие картину химического равновесия. В принципе, интенсивность минерагенеза всегда определяется этими двумя обстоятельствами: меняющимися термо- динамически1ии условиями и наличием транспортных процессов. Ранее вскользь затронуты причины изменения термодинамическР1х условий, имеющие природу релаксации энергии колебательных мод. Конечно, это лишь один из механизмов, среди которых и чисто гравитационные эффекты, и радиационный разогрев, и прочее, и прочее, поэтому в дальнейшем будет сделана попытка показать, что во многих сл)^аях морфологические особенности рельефа, связываемые с присутствием выделенной группы минералов, проще всего связать именно со структурой колебаний коры. Но прежде, чем приступить к этому, проанализируем наиболее известные общие схемы транспорта химических элементов.

Наиболее подвижным и наиболее распространенным из всех известных во Вселенной элементов является водород. Без его присутствия вообразить земные условия не представляется возможным как по характеру, так и по масштабам его участия в земных процессах. При этом именно он наиболее слабо «привязан»

Оценку потерь водорода земной атмосферой можно сделать следующим образом. Регистрируемая разность в поглощении и излучении солнечной радиации атмосферой составляет величину порядка 7 х 10’“* Вт. Эта мощность «потребляется» в основном парами воды. Отсутствие сколь-нибудь заметного векового разогрева атмосферы позволяет предполагать, что основным каналом потерь радиации в атмосфере является диссоциация воды, водород которой теряется в околоземном пространстве с интенсивностью около 10^° молекул в секунду, что соответствует нескольким миллионам тонн в год. Потери водорода частично компенсируются захватом магнитосферой протонов из «солнечного ветра». Но порядок потерь сохраняется. Возможность компенсации обратно пропорциональна квадрату расстояния между Солнцем и планетой. То есть Венера находится в гораздо более выгодных условиях, чем Земля и Марс. Скорость «убегания» от Марса к тому

же меньше земной в два с лишним раза. С другой стороны, интенсивность захвата протонов зависит от напряженности магнитного поля, которое, как показано в предыдущей главе, напрямую зависит от «качества» атмосферы. Поэтому по достижении некоторого порогового содержания воды в атмосфере ее разрушение приобретает нелинейный катастрофический характер. Длительное развитие атмосферы Земли возможно лишь при наличии достаточно мощного источника водорода в теле планеты. Природа такого источника достаточно неопределенна и широко не обсуждалась в связи с отсутствием заостренно сформулированной проблемы. Существует, тем не менее, гипотеза гидридного ядра, которое, в принципе, могло бы обеспечить длительное существование атмосферы и гидросферы. Есть и более экзотическая версия внутриземного протонного источника, основанная на идеях Н. Козырева о вещественной природе времени, откуда следует, что небесные тела являются генераторами вещества, и в первую очередь протонов. Тем не менее, наиболее реальным источником водорода является мантийное вещество, насыщенное водой. Помимо эманации водорода здесь, естественно, присутствуют и флюиды гвдроксила, также являющиеся высокоактивными агентами химических превращений и транспорта попутных элементов.

Существует ряд фактов, подтверждающих наличие масштабных эманаций водорода через кору Земли, обобщая которые Коржинский пришел к выводу о существовании кислотно-основных радиальных волн. Действительно, если речь идет об эманации протонов с очень высокой проникающей способностью, то в волнообразном изменении химической обстановки сомневаться не приходится. Но, с другой стороны, про- тонированный «поток» вещества есть не что иное, как электрический ток, поэтому волны Коржинского должны сопровождаться мощными электромагнитными процессами в земной коре. При некоторой кррггаческой плотности тока индуцированное им же магнитное поле сжимает его в тонкий разрядный шнур.

Явления, которые происходят при этом, близки по характеру к тому, что имел в виду А. А. Воробьев, формулируя гипотезу о подземной грозе. Мощные меняющиеся магнитные поля индуцируют вторичные токи, формируя спутники основного разрядного шнура в литосфере, а также являются причиной электромагнитных возмущений в прилегающей атмосфере. Токи, индуцированные в атмосфере, проявляются в виде зарниц и всполохов при низкой влажности, а при значительной проводимости воздуха возможно масштабное разделение электрических зарядов на облачных структурах, ре- лаксирующее затем в грозовых разрядах. Квазистацио- нарные протонные токи явным образом проявляются в структуре облаков и распределении осадков, электромагнитными аномалиями в атмосфере, но наиболее существенно влияют на состояние земной коры. В канале разряда развиваются высокие температуры и давления с одновременным механическим переносом вещества, обогащенного водородом. Следы разрядов неминуемо должны наблюдаться. И действительно, описанные условия хорошо известны специалистам, занимающимся синтезом алмазов. Исторически первые искусственные алмазы были получены при параметрах, соответствующих каналу разряда. Позднее технология была усоверщенствована, и давление с температурой были значительно снижены. Ныне алмазные пленки получают практически в условиях атмосферного давления и при обычных комнатных температурах. Общим для всех процессов является наличие углеводородов, обогащенных водородом. Условия в зоне стока, где происходит рассеяние тока по дневной поверхности, совпадают с технологическими. Ныне известно большое количество кимберлитовых трубок, строение которых совпадает с рассмотренной схемой. Можно, вероятно, прогнозировать наличие месторождений алмазов по характерной атмосферной активности в виде повышенного числа гроз и электромагнитных возмущений в приземном слое.

Наличие существенно ионизированных протонами потоков вещества в земной коре неизбежно связано с его электромагнитной сепарацией. Помимо чисто восстановительных условий, приводящих к выделению

Нефтегазоносные бассейны. По Н. Вассоевичу:

К Земле, поскольку скорость теплового движения его молекул близка ко второй космической. В этом отношении планеты земной группы по удержанию атмосферы находятся в критическом состоянии. Продукты фотодиссоциации паров воды в верхних слоях атмосферы образуют стабилизирующий от действия солнечной радиации экран в виде озонового слоя. Разрушение озонового слоя сопровождается резким увеличением поглощаемой атмосферой коротковолновой радиации, за счет чего происходит его восстановление, но ценой потери водорода. Впрочем, стабильность озонового слоя динамична по своей природе и обеспечивается в основном постоянно идущей диссоциацией воды, а соответственно, и потерей водорода.

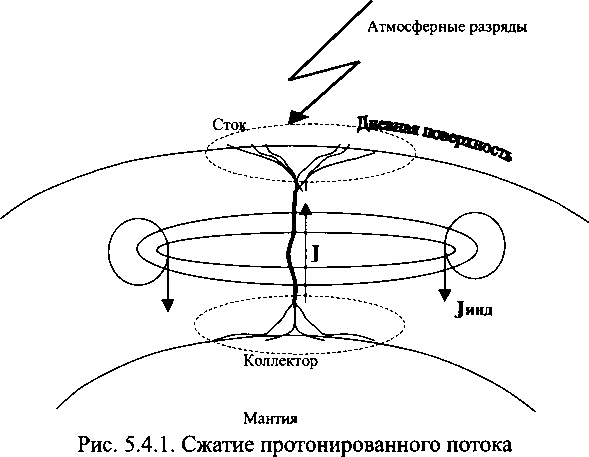
ряда веществ в элементарной, самородной форме, происходит и масштабное их концентрирование благодаря тому, что элементы с различающейся атомной массой «обладают» трубками тока различной кривизны. Этот процесс в полной мере аналогичен используемому в масс-спектрометрии, а при своей масштабности приводит к вполне реальному образованию рудных тел веерного типа, поскольку частицы с большей массой отклоняются в поперечном магнитном поле меньше, чем легкие, так что на рис. (5.4.2) > Mj.

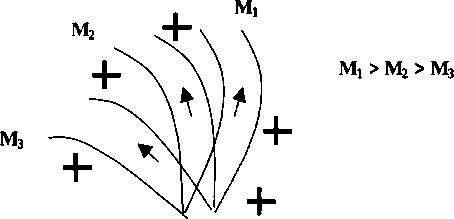
Рис. 5.4.2. Магнитная массовая сепарация (+ — силовые линии магнитного поля, направленные вглубь схемы)

Однако наиболее масштабные сепарация и преобразование вещества коры происходят все-таки благодаря химической активности и подвижности протонов. При этом восстановление карбонатных и окисных пород с образованием подвижных углеводородов и паров воды порождает гравитационную сепарацию продуктов гидролиза. Углеводороды и водяные пары, в свою очередь, мигрируют к дневной поверхности, накапливаясь под отложениями с низкой газопроницаемостью. Дальнейшая судьба углеводородных отложений связана с процессами гидрогенизации легких углеводородов и их частичной

потерей через перекрывающие отложения. Гидрогенизация приводит к образованию малоподвижного газоконденсата. Гидрогенизация возможна, естественно, лишь при наличии водородной продувки в условиях не слишком высоких температур. Ловушки углеводородов при значительных температурах обладают способностью крекинга с потерей легких компонент и концентрированием тяжелых. Длительный прогрев приводит к образованию вязкой битумизированной нефти и в конечном итоге к твердым углеводородам типа каменного угля. В свою очередь, тяжелые углеводороды и угли, включая законсервированные продукты экзогенного происхождения, могут вновь подвергаться гидрогенизации с образованием вторичных нефти и газа.

Рис. 5.4.3. Распределение угленосности, нефтегазоносных и железорудных бассейнов на территории бывшего СССР

Пояснения к рисунку 5.4.3

Угольные бассейны. По А. Матвееву:

Г — угольные бассейны и месторождения; 2’ — районы с преобладанием карбонатного угленакопления;

3’ — районы с преобладанием пермского угленакопле- ния; 4’ — районы с преобладанием нижнемезозойского угленакопления; 5’ — районы с преобладанием верхнеюрского и мелового угленакопления; 6’ — районы с преобладанием третичного угленакопления; 7’ — угленосные площади.

1. — западных областей Украины (Предкарпатье); 2 — восточных областей Украины (Дпепровско-Донецкая впадина); 3 — Крымского полуострова; 4 — Северного Кавказа и Дагестана; 5 — Мангышлака; 6 — Западной Грузии; 7 — Азербайджана; 8 — Восточного Прика- спия; 9 — Каракумов; 10 — Ферганской депрессии;
2. — Урало-Эмбинский; 12 — Волгоградско-Саратовский; 13 — Волго-Уральский; 14 — Ухта-Сибирской низменности; 15 — западной части Западно-Сибирской низменности; 16 — центральной части Западно-Сибирской низменности; 17 — северной части Западно-Сибирской низменности; 18 — Иркутской области; 19 — Усть-Вилюйской; 20 — о. Сахалин.

   Железорудные провинции. По В. Попову и Ю. Ста- рицкому:

   I — Карело-Кольская; II — Белорусская; III — КМА; IV — Украинская; V — Кавказская; VI — Уральская; VII — Арало-Тургайская; VIII — Центрально-Казахстанская; IX — Среднеазиатская; X — Западно-Сибирская; XI — Алтае-Саянская; XII — Приенисейская; XIII — Ангарская; XIV — Северо-Сибирская; XV — Забайкальская; XVI — Алданская; XVII — Северо-Восточная; XVIII — Дальневосточная; XIX — Камчатская.

   Параллельно с углеводородными процессами происходит эманация ювенильных вод преимущественно в

   паровой фазе. В этом состоянии вода обладает высокой способностью к растворению различных соединений, увлекаемых парами воды. Попадая в конденсационные ловушки с относительно низкой температурой, вода освобождается от части железа, формируя его в массивные отложения. Поскольку для углеводородного процесса и переноса железа исходная причина является общей — протонный ток, то совершенно естественно, что железорудные и углеводородные месторождения приурочены к месту локализации протонных эманаций через разломы в глубинных породах и образуют ассоциации типа древних: Уральской, Кузбасской, Донецко-Курской и др., более молодых — Бакчарско-Сибирской и совсем «юных» по контурам континентальных плит.

МЕСТОРОЖДЕНИЯ

Наиболее масштабные протонные потоки приурочены к тектоническим разломам и играют основную роль в сепарации и модификации вещества коры. Эти процессы обусловлены также свойствами верхних слоев коры (водогазопроницаемостью и пр.). Помимо различий этих свойств генетического характера вследствие дифференциации осадочного материала, существуют причины отличий эволюционного происхождения, например, разрывы и сдвиги сейсмической природы. Для процессов дифференциации вещества верхних слоев коры характерна приуроченность ее активности к нарушениям тектонической природы, связываемой с импульсными сбросами механических напряжений. Происхождение последних объясняют медленными процессами движения плит или их фрагментов под действием некоторых статических сил.

Между тем представляется, что природа статических сил заключена в самой сейсмичности, и последняя самодостаточна для понимания проблемы. Выше были рассмотрены некоторые особенности двумерных и трехмерных стоячих волн, которые, по сути, волнами уже не являются, приобретая черты стационарных объектов. Так, например, самая низкочастотная основная мода колебаний земной коры разбивает ее узловой линией на шесть отдельных фрагментов (рис. 5.3.1) по характеру стационарных напряжений, направленных в противоположные стороны. В зоне, прилегающей к узловой линии, происходит интенсивный вынос вещества из глубоких слоев коры и верхней мантии, образуя естественную границу для колебаний более высоких частот. Следовательно, основная мода колебаний для каждого из континентов индивидуальна и определена его границами. По сути, континент является автономным резонатором со своим набором стационарных колебаний, определить который в общем случае вряд ли возможно в силу неопределенности форм и размеров континентальных границ, несущих печать предшествующих тектонических процессов. Трехпетлевой контур замыкания поперечных колебаний основной моды планеты правильнее было бы привязать не к самим континентам, а к глобальным разломам, приуроченным к раздвигающимся зонам океанических впадин.

Рассматривая модель трехпетлевого контура, можно легко увидеть его чрезвычайную трансформность. Неизменным в нем остается наличие шести контуров и четырех точек самопересечения. Два контура являются «полярными» и ограничены двумя дугами, четыре другие — «экваториальные» ограничены каждый тремя дугами. Следует отметить, что в данном случае географический экватор практически ортогонален «тектоническому».

а) б)

Рис. 5.5.1. «Полярный» (а) и «экваториальный» (б) 10)нтуры

В формировании облика планеты большую роль играют не только поперечные, но и продольные сейсмические волны. История планеты, в которой, несомненно, присутствуют инверсии основной колебательной моды, подобные тем, которые характерны для электромагнитного поля, также влияет на совокупность деталей облика. Быстрые изменения конфигурации колебательных мод при инверсиях ведут к резкой смене макрорельефа, подъему океанов и опусканию фрагментов материков.

Обратимся вновь к проблеме формирования континентальных разломов. Ограниченный участок коры в некотором приближении можно рассматривать как ортогональную «плоскую» колебательную систему.

Напомним, что в формрфовании стационарных полей напряжений могут участвовать только колебания кратных и совпадающих частот, поэтому возмущения, вносимые в набор колебаний «несоверщенством» формы и рельефа континента, несущественны для решаемой задачи о конфигурации континентальных разломов. Основная мода предполагает наличие линейных и кольцевых структур разломов.

Если вдоль одного из ортогональных направлений возбуждена вторая мода колебаний с частотой ~ 2с0|, то набор конфигураций стационарных полей усложняется.

В случае, когда оба ортогональных колебания представлены удвоенной частотой, то есть собственными вторыми модами, стационарные поля будут вновь соответствовать формой (но не размерами и положением) основной континентальной, поэтому имеет смысл при со, = «2 говорить о первой моде, при 2c0j = (о^ — о второй и, наконец, при 3(Oj = (33^ — о третьей.

Четвертая и последующие моды, очевидно, будут представлены линиями с большими числами изгибов либо петлями, по количеству совпадающими с номером.

Несомненный интерес представляют дробные моды с кратными отношениями частот ортогональных колебаний:

Например, мода с частотами = (2 / 3) ©j ответственна за следующие типы стационарных полей.

Рис. 5.5.2. Формы дробной моды колебаний

Высокодробные моды образуют решетчатые структуры. Но, за редким исключением, рассмотрение их не имеет особого смысла по двум упоминавшимся выше обстоятельствам:

природа которых достаточно неопределенна и объясняется множеством частных гипотез. Поэтому общих закономерностей в расположении разломов и разрывов, а следовательно, и в распределении месторождений не просматривается.

Задача сводится к определению плоских форм (фигур Лиссажу), образующихся при сложении первых мод колебаний континента. Для изометрических фрагментов коры существует небольшой выбор форм стационарных колебаний основной моды от линейных, при нулевой разности фаз, до кольцевых.

С0| = (2 / 3) ©2? “ (3 / 4) ©2 и т. д.

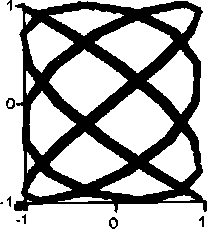
1. Высокие моды быстро затухают, отдав энергию основным, поэтому их вклад в формирование стационарных структур невысок;
2. Наличие нескольких одновременно возбужденных мод приводит к образованию бегущей волны, которая также не участвует в формировании стационарных полей.

Картину континентальных низкочастотных колебаний могут осложнять не только продольные волны, распространяющиеся с иными скоростями и формирующие собственную интерференционную структуру, но и другие причины. Основными среди них являются реликтовые особенности рельефа, образующие систему отражающих и преломляющих участков континентальной коры. Например, срединный океанический хребет после подъема станет континентальной горной системой и будет играть роль отражающего препятствия для континентальных колебаний. В этом случае континент разделен на две относительно самостоятельные колебательные системы, в пределах которых и будут формироваться континентальные разломы. Более того, реликтовых структур, вообще говоря, может быть много, и они могут значительно отличаться по возрасту.

Поля напряжений, формирующиеся под действием низкочастотной сейсмичности, как отмечалось выще, имеют противоположную направленность по разные стороны от узловой линии или поверхности. Для тонкой оболочки Земли, каковой является кора, это силы, «раздвигающие» либо «сжимающие» ее вблизи узловой линии. Вблизи последней представляют интерес и вертикальные напряжения, приводящие к подъему коры с одной стороны разлома и опусканию с другой.

ях поймы эта ювенильная вода, конденсируясь, играет далеко не второстепенную роль в питании реки.

Форма великих рек, абстрагированная от локальных деталей, совпадает с очертаниями фигур Лиссажу. Действительно, несмотря на то что существует множество причин, препятствующих реализации колебаний континентальных плит в идеальном аналитическом варианте, русла великих рек тяготеют к этим формам. Причем если «прямолинейные» русла достаточно редки (Амазонка, Нил, Енисей), то реки S-образной формы широко распространены. Дело в том, что S-образная форма характерна как для второй, так и для третьей моды. Если для последней она соверщенно естественна при нулевой разности фаз, то для второй реализуется за счет того, что одна из ветвей двухпетлевой фигуры Лиссажу, как правило, выражена хуже другой.

Причиной этого является то, что в приведенном рассмотрении не учтен вертикальный компонент колебаний. По этой же причине в рассмотренной схеме отсутствует разница в форме устьев и истоков. Характерными примерами «восьмерок» второй моды являются стрзчстуры бассейнов Волги и Оби. Последняя «замыкается» руслами рек Таз и Иртыш. Волгу «замыкают» Урал и Кама.

Неявность «замкнутости» контура речного русла возникает вследствие того, что узловая линия колебаний либо уходит в основание плиты, пракгачески в верхнюю

мантию, либо поднимается в верхние слои коры. И в том, и в другом случае планарные напряжения легко релакси- руют и не приводят к существенной раздвижке.

Отметим, что наиболее высокочастотные колебания могли бы организовать решетчатые структуры, но в силу обсуждавпшхся выше причин не реализующиеся на значительном пространстве, тем не менее, образуют «обрамления» для основтк мод, проявляющиеся в виде ритмически расположенных устьев притоков великих рек. Для правобережья Оби это реки Томь, Чулым, Кеть, для Енисея — Нижняя и Подкаменная Тунгуски, Ангара.

Предлагаемый здесь подход к анализу тектонических процессов не отвергает известные и признанные гипотезы, а напротив, дает возможность выявить причины накопления и сброса напряжений в земной коре. Кроме того, в приведенной модели появляются достаточно четкие ориентиры для определения структуры тектонических разломов, закономерностей рельефа дневной поверхности и распределения месторождений полезных ископаемых.

Выше в качестве одного из главных механизмов дифференциации вещества была рассмотрена «продувка» земной коры эндогенным водородом. Естественно, что благодаря большой подвижности водорода его эманации, в принципе, повсеместны. Однако кинетика процесса усиливается в зоне разлома, вследствие чего наиболее активная дифференциация вещества происходит именно в этих областях. Наиболее масштабные продукты дифференциации, как отмечалось выше, — это месторождения углеводородов и железных руд. Но, вероятно, еще больший объем составляет вода и как результат восстановления кислородных соединений, и, вероятно, выделяющаяся из вещества мантии и нижних слоев коры.

Дальнейшая судьба продуктов восстановления определяется их подвижностью и свойствами вымещающих пород. Практически непременным обстоятельством для накопления углеводородов считается наличие ловушек, перекрытых отложениями с низкой проницаемостью для паров, с чем трудно не согласиться. Можно предположить также, что ловушками могут служить вечномерзлые грунты. Немаловажную роль играет и форма ловушек в виде куполоподобных образований, складчатых и барханных форм поверхностей осадочных слоев, а также наличие среди них легкопроницаемых, в которых и накапливаются подвижные углеводороды.

Если учесть, что один из краев разлома испытывает поднимающие, а другой — опускающие напряжения, то становится ясно, что условия для аккумуляции углеводородов для них существенно отличаются. Действительно, с одной стороны в результате изгиба слои принимают положительную, а с другой — отрицательную кривизну.

Одна сторона аетивно поглощает продукты эманации, а другая такой способностью не обладает. Благодаря на- личшо локальных (вблизи разлома) и региональных систематических понижений чехла продукты водородной продувки могут мигрировать от разлома на значительные расстояния. Естественно при этом, что вещество легкопроницаемых слоев и — в несколько в меньшей степени — труднопроницаемых претерпевает существенное изменение. Поскольку мигрирующая вода (или пары) часто проявляет слабокислые свойства, то силикатные породы чехла растворяются с образованием щелочей, гидрокремнезема и глиноземистых соединений. А так как все они обладают разной подвижностью, то возникают условия для их разделения с образованием обогащенных участков слоя, которые в будущем могут оказаться вблизи дневной поверхности в качестве доступных месторождений. Локализация современных месторождений соды, глинозема, кварцита и других минералов из этой же группы эндогенных продуктов тяготеет, как правило, к предгорьям. Это дает основание для гипотезы их гидротермального происхождения, приуроченного к периоду магматической активности комплекса. Вероятно, исключить такие процессы невозможно, однако из рассматриваемой модели можно сделать и другие выводы. Эволюция планетарных и континентальных разломов, надо полагать, проходит в несколько этапов. Первый из них длится до момента начала разрушения фундамента коры, то есть это период упругих колебаний. Второй этап, к которому относится вышеприведенное рассмотрение эндогенных процессов, длится до тех пор, пока остывающая за счет эманаций через разлом мантия не начинает всплывать вследствие уменьшения плотности. Начинается третий этап, в течение которого продолжается всплытие с разгрузкой давления, а следовательно, с возникновением перегрева за счет тепла фазовых переходов. В течение этого магматического этапа локальные очаги перегрева затрагивают и массивы дифференцированного вещества верхней коры, вовлекая его в маг- матогенный метаморфизм, в процессе которого карбонатное железо, например, может трансформироваться в магнетит. «Вскрытые» углеводородные месторожденрм быстро теряют легкие компоненты, превращаясь в битумы и угли. С прекращением магматической активности всплытие еще не заканчивается. Это четвертый этап эволюции разлома и прилегающих к нему метаморфических месторождений разного типа. С завершением тектонической активности начинается пятый этап — активного выветривания с превращением горного хребта в структурный реликт континента. К такого рода структурам относится Урал, расположенный на месте одного из древнейших разломов. Внимательное исследование Евроазиатского континента показывает, что первая мода еще не изрезанной плиты должна образовать структуру кольцевого или линейного типа в центре материка. Вероятнее всего, Урал входит именно в кольцевую структуру, элементами которой являются, помимо него. Среднесибирское плоскогорье. Казахский мелкосопочнрпс и отчасти северные отроги Алтая и Саян.

Эволюция колебательных структур коры от разлома до реликта показывает, как эндогенные процессы дифференциации переходят в гипергенные через фазу магматической активности. Масштабы гипергенной переработки вещества верхней коры ничуть не меньше эндогенных. Более того, в глубине осадочного чехла современные эндогенные процессы перерабатывают вещества, уже побывавщие в гипергенном цикле, из чего следует, что дискуссия между сторонниками гипотез биогенного и эндогенного происхождения углеводородных месторождений особого смысла не имеет. Выше уже упоминалось, что процессы синтеза углеводородов из карбонатных пород при водородной продувке параллельны гидролизу и гидрогенизации углистых отложений и законсервированной биомассы. Естественно ожидать, что наиболее значительные масштабы современных процессов дифференциации вешества коры характерны для планетарной узловой линии. Напомним, что она и проходит по: срединному Атлантическому хребту. Северному Ледовитому океану (который в свете рассматриваемой модели правильнее было бы называть Северным Средиземным морем), далее идет вдоль восточного побережья Азии, огибает Австралию, затем пересекает Панамский перешеек и экваториальную часть Атлантики, отсекает Африку от Евразии по Средиземному морю и суше Малой Азии, выходит в Индийский океан, затем мимо южной оконечности Америки входит в Тихий океан, вдоль западного побережья обеих Америк подходит к Юго-Восточной Азии, пересекает Индийский океан и замыкается в Атлантическом.

Узловая линия (глобальный линеамент) в некоторых частях сопровождается раздвиганием коры, а в других — сжатием, в результате чего одна часть «ныряет» под другую. Очевидно, что планетарный разлом земной коры развивался вдоль узловой линии с неодинаковой скоростью, поэтому мы можем наблюдать, следуя по нему, большинство фаз его эволюции. Участки, проходящие вдоль Срединного Атлантического хребта, находятся на этапах всплытия и магматической активности. К этим же этапам относятся и участки, окаймляющие Юго-Восточную Азию, а также участок, проходящий через Средиземное море. На этой же фазе находится фрагмент узловой линии, проходящий вдоль западного побережья Америки. В фазе остывания верхней мантии находятся участки, разделяющие Евразию и Северную Америку, Австралию и Антарктиду, а также участок, проходящий по суше Малой Азии, где как раз сконцентрированы гигантские запасы нефти. Природа шельфовых месторождений объясняется их нахождением в области перегиба коры в зоне узловой линии и, соответственно, большой способностью к захвату углеводородов, мигрирующих затем в наклонных слоях.

Континентальные разломы также проявляют высокую активность в переработке вещества коры. Широко распространены углеводороды, например, в бассейне реки Обь. Здесь же находится крупнейшее железорудное тело. Кольцевая структура реликтового разлома, обрамляющая Обский бассейн, представлена древними выветренными массивами с обилием метаморфи- зованных пород и железных руд, ассоциированных с месторождениями углеводородов Урала — Казахстана — Кузбасса — Красноярья.

Таким образом, главной закономерностью в распределении месторождений полезных ископаемых является их приуроченность к муаровому узору интерференции собственных колебаний земной коры. Возраст и минеральный состав месторождений определяются эволюцией разлома, от формирования напряжений в зоне узловой линии стоячих волн до разрыва плиты, с последующим образованием речного бассейна, а затем и горного массива, формой своей повторяющего реликтовый разлом.

В рассмотренной геодинамической схеме нетрудно заметить реализацию голографических принципов экологической парадигмы. Некая «живая» среда, например, кора Земли, формирует внутри себя такие собственные структуры, которые на некотором этапе раз- ВИТР1Я превращаются в «самодостаточные» элементы, разрушающие целостность среды. Однако, достигнув определенного состояния, эти элементы с лихвой восстанавливают «разрушенное» уже собственной активной «деятельностью».

Голографические принципы, оставляя в стороне природу пространства и времени, обладают, тем не менее, достаточной универсальностью для интеграции комплекса знаний, полученных в периоды расцвета классической и неклассической науки и являются естественно-научной основой общей экологии и ее частных направлений, среди которых особую значимость имеет комплекс представлений о Земле — геоэкология.

Глава 6.

Все великолепие окружающей Реальности основывается на весьма простых принципах. И хотя в предьщу- щих главах использован иногда весьма специфический язык, скажем, типа птичьего, за что автор приносит свои извинения, надеюсь, за этим не потерялось ощущение универсальности голографического описания Мира.

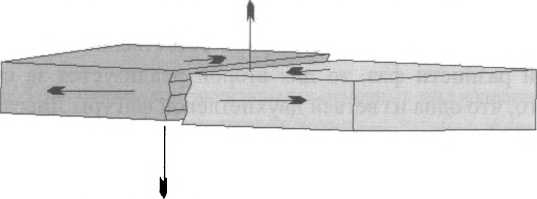
Рис. 5.5.3. Напряжения в зоне разлома

Разлом континентальной плиты сопровождается разрывами и разрущениями осадочного чехла, вследствие чего процессы низкочастотной квазистационар- ной сейсмичности принимают активное участие в формировании поверхностного рельефа. Рано или поздно напряжения «узловой линии» приводят к разделению плиты и раздвижке ее фрагментов, вследствие чего на поверхности реализуется провал, декорирующий линию разлома, становясь, как правило, ложем реки. Этому способствует и то обстоятельство, что через разлом и нарущенный осадочный чехол начинается интенсивная эманация водорода в форме продуктов восстановления, в первую очередь воды. В приповерхностных ело-

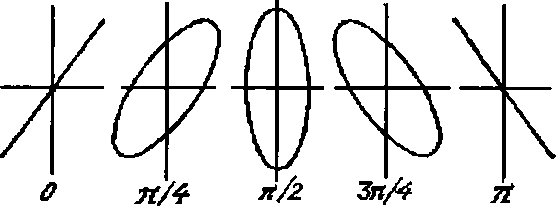
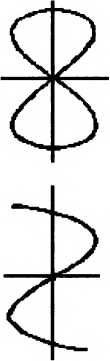
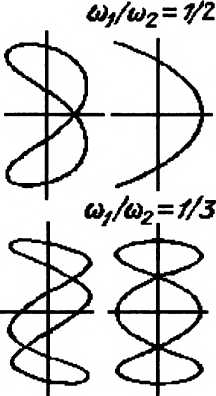
Рис. 5.5.4. Формы континентальных основных мод ю)лебаний

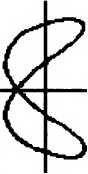
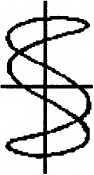
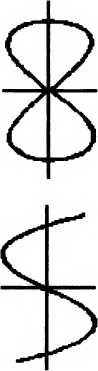
Рис. 5.5.5. Русла рек, декорирующие разломы

Рис. 5.5.6. Изгиб чехла в зоне разлома

ОДНООБРАЗИЕ (ПРАВЬ)

БИОСФЕРА

Возраст планеты оценивается обычно в 4,5 миллиарда лет. Примерно таков же возраст Солнечной системы. В то же время возраст Вселенной от мифического Большого Взрыва составляет примерно 25 миллиардов лет (2,5-10“* лет). Весьма любопытно, что экспериментальные оценки времени жизни протонов дают величины порядка 10^® лет. Возникает вопрос: то ли Вселенная очень молода вместе со своим водородом, то ли означенного Взрыва не было?

Кстати, в событии подобного рода ничего невероятного нет. Мы теперь уже знаем, что вакуум не пуст и обладает достаточно высокой плотностью энергии. Но, с другой стороны, мы знаем, что структура Вселенной могла начать свою эволюцию не с высокоэнергетичных событий, а совсем наоборот, с низкочастотных колебаний (глава 2). Тогда вопрос о возрасте Вселенной приобретает некоторую расплывчатость вместе с корректностью утверждений о разбегании звездных систем.

Да и с чего это вдруг, куда ни глянешь, дальние Миры разбегаются именно от нас как черт от ладана? Основанием для утверждений о разбегании звезд является эффект смещения линий спектров в красную сторону. Отсюда на основе эффекта Доплера и делается такой вывод. Но это не однозначный вывод, поскольку к смещению спектров могут приводить и другие явления. Например, правило аддитивности частот, то есть возможность их сложения и вычитания в оптически активных средах, а вакуум — это хоть и разреженная, но среда, наполненная водородом и пылью.

Но мы отвлеклись от темы параграфа, даже не коснувшись ее, хотя теперь можем соотнести возраст биосферы с упомянутыми величинами. Жизнь на нашей планете удивительно молода. Если не брать во внимание споровые формы (нельзя сказать, что это совершеннейший примитив, но уж сильно отличается от нас, привычных), то активная фаза развитрм жизни (подчеркнем: органической, углеводородной) — всего-то какие-то 600 миллионов лет. Это было недавно. И это было, вероятно, какое-то космическое событие, помасштабнее того, что спустя несколько сот миллионов лет привело к вымиранию динозавров.

Существуют гипотезы о том, что 600 миллионов лет назад наша планета скачком изменила среднюю плотность и довольно сильно прибавила в размерах. Одновременно на Земле появилась вода. Это достаточно хорошо стыкуется с гипотезой Ларина о первоначально гидридном веществе планеты. Большинство веществ действительно могут в определенных условиях (космический холод) растворять значительные количества водорода, образуя весьма плотные гидриды, которые затем, при нагревании, отдают водород и снижают плотность.

Гипотеза Козырева утверждает, что вещество рождается из времени и основная масса новорожденного представлена водородом. Разовьем эту мысль и вообразим, что наша Галактика 600 миллионов лет назад вошла в несколько иной временной континуум и стала интенсивно генерировать водород. Опять же, если времени «стало больше», то пространство стало разреженней (см. гл. 3). Вот и причина того, что Земля «распухла». Но если всерьез, то здесь нет, опять же, ничего невероятного. Та же самая мысль может быть выражена на несколько ином языке. Взаимодействие между частицами вещества (см. гл. 4) имеет резонансный характер, параметры которого определяют плотность. В выражение для резонансных частот

Но, впрочем, это все те же эффекты Времени. Тем не менее, историческая геология и палеонтология собрали массу доказательств того, что современная биосфера родилась примерно 600 миллионов лет назад.

Биосфера — это невероятно тонкая по планетарным масштабам пленка живого вещества. Наиболее плотный ее слой составляет от силы первые десятки метров (лес). Конечно, споры сосны, например, могут забираться и в достаточно высокие слои атмосферы, но это не есть сама жизнь. Пыль. Правда, на высоте двенадцати с половиной километров летчики встречают иногда гусей во время перелетов. Чем они там дышат и на что «опираются»? В водоемах тоже обитают ныряльщики, достигающие километровых глубин. Но это уник)^ы. А в целом сопоставим: 10-^20 метров — биосфера и почти 6 378 000 метров — радиус Земли!

Велика ли роль биосферы для планеты? Оказывается, биосферные процессы столь стремительны, что в ее обороте на протяжении всего-то 600 миллионов лет побывало вещества по массе раз в 15 больше массы земной коры! И на чем, спрашивается, зиждется эта невероятная сила? По меркам человека «просвещенного» — на химере. Вся сила биосферы происходит от света? От воды? И от углекислого газа, которого в атмосфере ничтожные три десятых доли процента! А вот на же тебе.

Биосфера находится на границе между литосферой и атмосферой и поэтому очень сршьно зависит от процессов, в них происходящих, хотя и сама играет роль их мощного преобразующего фактора. Очень часто к числу верхних геосфер относят и гидросферу, но водная оболочка как бы объединяет литосферу и атмосферу, контролируя множество процессов. О значении воды для биосферы и говорить излишне.

в предыдущей главе говорилось о том, что собственные частоты электромагнитного поля планеты удивительным образом совпадают с важнейшими биологическими частотами. «Верхняя» грашща низкочастотного окна прозрачности атмосферного волновода (7,5 Гц) соответствует ритмозадающей частоте работы головного мозга и сердечной мьппцы большинства теплокровных животных. Предположительно можно говорить, что именно этим ритмом вся биосфера обращается в единый организм.

Следуя традиции, в рассказе о биосфере далее следовало бы начать повествование о переносе вещества и энергии, аккумуляции их и рассеянии, значении биологических процессов для минерагенеза и т. д., и т. п. Но эти вопросы довольно детально описаны во множестве учебников, а основной задачей нашего экскурса компиляция не является.

V ^0^

входит электрическая постоянная е^, и если она меняется в пространстве Вселенной, то и плотность планет и звезд, путеществующих в ее просторах, также должна меняться. Причем меняться должны и особенности химических взаимодействий. Что-то должно распадаться, а что-то новое образовываться.

ПЛОЛЫ

Если проточастицы вещества есть не что иное, как интерференционные решетки электромагнрггного поля, то более масштабные тела — это тоже решетки, но в узлах их «уютно» размещаются вещественные структуры предыдущих уровней. Поэтому устройство «массивных» тел, по сути, ничуть не сложнее структуры элементарных частиц. Естественно, и не проще. То есть все многообразие окружающей реальности строится на достаточно простых принципах, и было бы странно не заметить за разнообразием форм однообразия структуры и морфологии.

Электромагнитное поле в нашем изложении предстает как динамический процесс превращения Времени в Пространство и Пространства во Время. Образование

стационарной полевой структуры есть результат некоторой суперпозиции таких процессов, подчиняющейся простому принципу кратности либо совпадению частот. И хотя поле по-прежнему можно представлять как динамический процесс, но только в проекциях на какие-либо направления в Пространстве. В целом корректнее говорить о геометрии времени и плотности пространства.

В третьей главе мы обсуждали этот вопрос, рассматривая проблему распространения поля, и пришли к выводу, что наиболее «подходящей» поверхностью для описания волнового фронта является поверхность тора. Однако рассматривать распространение поля как монотонный процесс, вообще говоря, нельзя. Действительно, в достаточно удаленных от источника Поля областях нам представляется, что характер его не изменяется по мере удаления.

Но если вернуться к проблеме волновой поверхности, то становится ясно, что и это не так. Дело в том, что по мере удаления от источника в любом случае у волновой поверхности меняется кривизна. Она уменьшается в направлении распространения. И в соответствии с геометрическим определением кривизны мы уже отмечали, что она имеет смысл частоты. Следовательно, вдали от источника наблюдаемая частота Поля в каком-то диапазоне расстояний будет уменьшаться. То есть будет наблюдаться эффект красного смещения, вовсе не связанный с эффектом Доплера. Проблема «разбегания» Вселенной, вероятно, просто надумана.

Вблизи источника события будут более разнообразны, поскольку изменения кривизн волнового фронта неизбежно приведут к ситуации, когда в сохраняющемся произведении полной кривизны

возникнут кратные соотношения, такие, что п X к, = m X Ц,

Очень часто несколько «простых» форм совмещены. Например, в листе почти всегда встречаются древовидные прожилки. А иногда и все дерево напоминает лист. И вот уже за всем многообразием форм мы различаем всего-то несколько основных типов. Упомянуты игольчатые и листовые. Древовидные предстают как совокупность «иголок». Мы смело можем включить в эту группу форм все хвойные, но вглядимся под ноги и увидим, что таковы же, в принципе, формы хвощей, укропа, тмина.

Листья часто изогнуты. Причем, как правило, в двух направлениях. Вглядимся пристальнее и обнаружим, что листья повторяют какую-то известную поверхность. Вернее, фрагменты поверхности. Поверхности полярного тора. Возьмем лист герани или клена. Если подобрать тор соответствующих размеров, то листья аккуратно на них улягутся. Еще более поразительно соответствие поверхности полярного тора некоторых цветков, например, лилий. Ну а уж если они до конца распустились, то лепестками своими охватывают всю поверхность тора, правда, с пробелами.

Так же с пробелами, но не поверхности, а всего тела полярного тора, выполнены кусты и деревья. Вспомним отдельно растущие особи. Освободим мысленно корни от почвы и согласимся. Может быть, слегка удивимся, обнаружив, что много раз видели, но не рассмотрели, что деревья подобны яблоку.

Яблоко — непременный атрибут всякого почти Святого Писания, включая сказки. Вспомните! Ева надку- срша всего лишь плод с дерева познания Добра и Зла. А Адам доел. Испил, так сказать, до дна чашу. О чашах разговор особый. Но удивительно! Яблоко — действительный образ полярного тора. И эту же форму имеет и тыква, и вишня, и помидор. Слегка вытянуто и иногда деформировано «яблоко» огурца и баклажана, но тоже легкоузнаваемо. Ягода малины — тоже полярный тор, но обратите внимание, он сложен из других маленьких полярных торов. И даже корзинка хорошо вызревшего подсолнуха, выгибаясь давлением семян, превращается в поверхность полярного тора.

Однако такие же формы распространены не только в растительном сообществе. Яйцо курицы и икринка лягушачья. Но и плод в утробе матери! Голова человека и большинство внутренних органов: почки, сердце — также повторяют форму полярного тора.

а) 6) в)

Возможно, это и есть одно из основных отличий животных от растений. Не единственное. Например, можно указать на поразительное различие в питании. Вернее, в пищеварении. У животных оно происходит внутри: желудок, кишечник и прочее. У растений «желудок» расположен снаружи. Он в некотором смысле открыт вовне. Переработка веществ происходит рядом с корнями. Но и это различие обращается в тождество тем, что и животные, и растения переваривают пищу не сами (точнее, не вполне сами), а с помощью миллиардов других существ. Симбиотическая флора и фауна желудка и кишечника перерабатывают для нас то, что мы проглотили. Без этого сообщества (медики называют такой случай термином «дисбактериоз») летальный исход гарантирован.

В прикорневой почве растений развивается совершенно необходимая для их жизни грибница (микориза). Последняя питается сахарами (продукт фотосинтеза), но и сама активно питает растение минеральными веществами и, что весьма важно, соединениями азота. Грибница чахнет без дерева, но и дерево гибнет без нее. Однако мы отвлеклись, хотя тема очень интересна в экологическом смысле.

Еще один важный, хотя в некотором смысле промежуточный и не вполне характерный, случай представляет метаморфоз некоторых насекомых. Личинка-гусеница, накопив достаточное количество жиров и протеинов, обволакивает себя оболочкой из паутины в форму опять же яйца. Затем гусеница сгнивает или, если хотите, растворяется, превращаясь в плазму. Совсем похоже на яйцо с его белково-жировым содержимым.

Обратившись вновь к торовидной форме дерева, мы и его должны отнести к некоторой разновидности плода. Разве не чудо, как сказано в Писании, что из семени горчичного, подобного пылинке, произрастает куст, подобный дереву? Но у дерева плод ажурный: ветви, листья. Здесь же мы имеем ситуацию, в которой полярный тор плода рождается не из чрева, а «собирается» из внешней субстанции. Полезно вспомнить, что полярный тор — это конструкция из структуры пространства, что в современной науке именуется электромагнитным полем. Поэтому тор есть продукт интерференции в виде сетки из узлов и пучностей стоячих волн. Мы это уже обсуждали и пришли к выводу, что такие «узлы» обладают признаками вещества. По крайней мере, они не нейтральны в зарядовом (в электрическом смысле) отношении. И, естественно, для их нейтрализации воспользоваться ионами уже существующего реально вещества. Интерференционная картина дерева нейтрализуется и одновременно усиливается. Заполняются всё более дальние порядки интерференции. Дерево растет. Но вначале было семя. Семя это не плод. Внутри плода может быть и несколько семян.

Дерево-плод может и не нуждаться в семени-причине. Тривиально — вегетативное размножение, черенкование, например. Еще более «простая» ситуация может возникнуть при электрическом разряде, если в результате интерференции генерирующихся при этом электрических и магнитных полей образуется стацио

нарная пространственная структура. «Узлы» ее заполняются ионами газа и заряженной пылью, декорируют невидимое поле сиянием плазмы. Шаровая молния. Или еще более впечатляющие структуры и образования, подобные, например, тунгусскому феномену 1908 года. На механизм образования таких объектов, через заполнение узлов «квазикристаллической электромагнитной рещетки» возбужденного пространства реальным веществом, несколько десятков лет назад указывал томский профессор В. Н. Сальников. По его мнению, это могут быть и весьма плотные образования, сопровождаемые менее эффектными событиями, нежели тунгусский феномен, но весьма впечатляющие «мгновенными» исчезновениями значительных количеств вещества либо, наоборот, загадочным появлением его.

Рассматривая квазикристаллические структуры поля в последнем случае, мы вплотную приблизились к проблеме яйца, которое «вперед курицы». Напомним, что в первых главах мы обсуждали эволюцию поля и припши к «геометрическому» выводу о возможности генерации высокочастотных компонент поля. Эта возможность формально является следствием Фурье-разложения импульса на бесконечный набор гармонических частот, то есть таких, которые заранее соответствуют условию образования стационарных структур. С геометрической точки зрения каждой компоненте поля соответствует некоторый вектор. И если мы имеем хотя бы пару векторов, что для электромагнитного поля есть почти всегда, то автоматически получаем все тот же бесконечный набор гармонических частот. Причем в этом случае каждой частоте соответствует некоторый вектор из совокупности перпендикулярно ориентированных наборов. Поэтому условия Лиссажу выполняются автоматически для большинства компонент. Образование стационарных структур переводит поле в состояние деструктивной интерференции, а в рассматриваемой ситуации можно считать попросту, что поле обращается в протовещество. Тем самым в спектре Фурье-разложе- ния поля большинство компонент взаимовычитаются, и в гармоническом ряду остаются, как правило, только «хвосты» наиболее низкочастотных слагаемых. Но образовалось «протояйцо».

Обратимся наконец к эволюции «яйца». Известно, что яйцо в холодильнике может храниться очень долго без явных изменений. Поразительно долго могут сохранять всхожесть семена злаков, например. Сотни лет. Было даже сообщение о тысячелетних сроках хранения. В прохладном месте долго не портятся яблоки, помидоры и иные растительные «яйца».

Но если плоды помещены в тепло (инкубатор), то они быстро дозревают и прорастают. Цыпленок разбивает скорлупу и является Миру. Из невзрачного червячка, опутавшего себя коконом шелковой нити и растворившегося в плазму, является Миру великолепная бабочка. Что происходит?

Если провести химический анализ яблока или помидора, только что снятого с дерева или куста, то выявится бедность состава высокомолекулярными соединениями: белками и жирами. Можно, например, для убедительности сорвать зеленые плоды и убедиться, что, кроме углеводов, там почти ничего нет. Но тот же плод, дозревая в тепле, а такой прием очень часто используют на практике, покажет, что в его химическом составе в заметных количествах появились белки и жиры. Это результат синтеза, который осуществляется самим плодом.

В плоде-яйце развиваются (иногда в единственном числе) семена. Если говорить о яблоках и других овощах-фруктах, то стоит зазеваться — и они прорастают. Важнейшее значение здесь имеет сохранность плода. Повреждена скорлупа — и яйцо протухнет. Повреждена кожица плода — и он сгниет. Разорван кокон — и плазма высохнет, а бабочка уже не появится.

Как мы ранее выяснили, динамическая голограмма, соответствующая реальной частице, представляет собой тороидальную электромагнитную систему и обладает собственной внутренней структурой из областей конструктивной и деструктивной интерференции. Воспользуемся упрощенной схемой в виде развертки поверхности полярного тора на плоскость.

Приведенный вариант анализа процессов «внутри» плода показывает, что одновременно с полями и структурами вторичной интерференции вне основного «тела» образуются и «узлы» внутри него. Наружные структуры, естественно, являются низкочастотными, то есть низкоэнергетическими, в силу того, что образованы за счет интерференции «вычитания» частот. Дело в том, что «узлы» основной структуры не обладают «единственной» частотой. Поэтому возникают их разности. Но внутренние «узлы» вторичной интерференции возникают за счет суммирования частот и являются более высокоэнергетическими по отношению к «узлам» основной структуры.

Близкой аналогией к рассмотренным процессам является оптическое явление смещения спектра люминесценции по отношению к спектру ее возбуждения. В нормальных условиях, как правило, преобладает так называемое стоксово смещение (по имени оптика Stocks). Но для некоторых веществ либо экзотических условий опыта наблюдается и антистоксово смещение за счет сложения частот возбуждающего света и частот собственных колебаний фотоактивных центров.

Так, в нашем случае, если пространство низкочастотных внешних структур «заполнено» сторонним излучением с близкими частотами, то узлы вторичной интерференции для «осуществления своего гомеостаза» обладают единственной возможностью скачать часть энергии в высокочастотную область. За счет этого начинают развиваться внутренние узлы. Это и есть семена плодов.

Плоды растений имеют короткий век, но успевают обеспечить условия для развития семян. Теперь вообразим в качестве плода протон и вспомним, что протон даже в свободном состоянии существует невероятно долго. Что же касается его внутренней структуры, то можно предполагать ее необычайную развитость и великую энергетику. Возможно, равноценную нашей Вселенной.

kj X Ц = inv

где пит — целые числа. Это соответствует условию образования стационарной структуры Поля, и если оно выполняется для некоторой области поверхности волнового фронта, то именно эта область и будет представлять новую форму вещественного проявления. Разнообразие форм действительно велико. Это игольчатые и древовидные, плоские и изогнутые листья и т. д., и т. п.

Рис. 6.1.1

спаржи и многих других растений. Но и листья — по сути своей те же «иголки», соединенные перепонками.

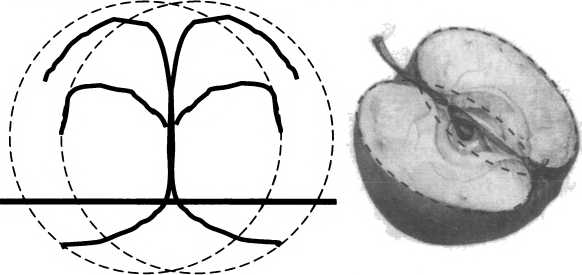
Рис. 6.1.2. Дерево — тор — яблоко

Рис. 6.1.3. Эмбрион человека: а) деление клетки; б) третий день после оплодотворения; в) десятая неделя беременности

Конечно же. Вы, мой внимательный собеседник, тут же припомните и чуть приплюснутые шары планет. Наша Земля именно такова, и ее форма имеет специальное название — геоид. Напомним, что в Святых Писаниях упоминается и форма Вселенной — яйцо.

Перейдем далее к исследованию бытия (судьбы ли?) плодов. Но прежде вспомним, откуда берутся плоды, т. е. вернемся к обсуждению сакраментального и «бес-

смысленного» вопроса о том, что вперед: яйцо или курица? Вопрос, конечно же, не прост. Яйцо, икринка, плод человеческий появляются из утробы материнской. Яблоки и прочие растительные плоды произрастают на ветвях деревьев и кустов.

Рис. 6.1.4. Развертка контура импульса на плоскость

Области конструктивной интерференции представляют собой подобие виртуальных частиц, описанных в рассмотренном выше случае. Вектор результирующей напряженности поля в течение некоторого времени вра-

щается, мало изменяясь по модулю, затем уменьшается до нуля и «возникает» в следующей области конструктивной интерференции. В целом картина весьма напоминает елочную гирлянду «бегущий огонь», имитируя орбитальное движение виртуальной частицы. Сами по себе области конструктивной интерференции являются когерентными, но отличающимися фазой, источниками поля, и это «вторичное» поле создает собственную интерференционную сетку как внутри системы, так и в ближнем ее окружении. Упрощенную структуру вторичной интерференционной картины можно построить, воспользовавшись тем обстоятельством, что наибольшую когерентность поля двух и более источников проявляют вдоль оси, проходящей через эти источники. Проведем ось через пару крайних областей конструктивной интерференции, а затем построим все остальные, ее пересекающие, например, справа от рисунка.

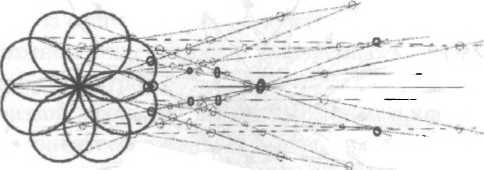
Рис. 6.1.5. Внешняя вторичная интерференция

Аналогичным образом строятся оси и для всех остальных пар. В результате получается нечто, весьма напоминающее венчик из лепестков подсолнуха или ромашки.

«Венчик» и первичная интерференционная структура, собственно, и образуют элементарную голограмму, причем «лепестки венчика» могут иметь значительную протяженность, в несколько раз превосходящую харак-

терные размеры первичной структуры. Мы рассмотрели здесь только те фрагменты вторичной интерференционной картины, которые достаточно просто построить. Но уже и такой упрощенный вариант в целом характеризует структуру поля в ближней зоне. Если продолжить построение с учетом того, что и вторичная структура является источником полей, то можно получить непрерывную связь розеток, совершенно идентичных тем, что возникают во фрактальной теории. Это и неудивительно, поскольку в обоих случаях используется общая аксиоматическая основа, за тем лишь отличием, что во фрактальной теории она используется в неявной форме, ограничиваясь понятием комплексного числа.

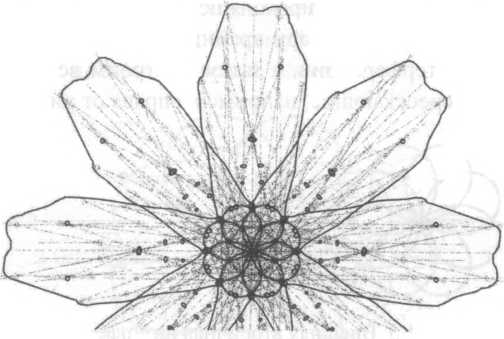
Рис. 6.1.6. Структура вторичной интерференции

«Непрерывная» интерференционная сетка, возможно, реализуется в каких-то случаях, и ее вполне можно связать с определенными структурами. Однако на самом деле картина в части конструктивной интерференции вовсе не выглядит непрерывной, образуя пространственно-замкнутые динамические структуры.

Хотя природа всех взаимодействий едина и в конечном итоге определяется электромагнитными колебаниями, но в частных случаях знание ее вовсе не обязательно, поскольку определяющим является сам механизм интерференции колебаний. В большинстве случаев можно воспользоваться хорошо разработанными моделями механических осцилляторов и волновых процессов в распределенных системах или макрообразованиях.

1. ЯВЬ. НАВЬ. ПРАВЬ

   Культ этих трех ипостасей Реальности восходит к древней ведической философии, которой, вероятно, уже многие десятки тысяч лет. Но они легкоузнаваемы и ныне, если мы прониклись пониманием комплексности окружающего нас Мира. Действительно, Явь — это то, что явно наблюдаемо, т. е. вещественно. Навь (за этим термином хорошо слышится «наваждение») — реальность, скрытая от непосредственного наблюдения, о которой можно лишь догадываться — мнить. Но в нашем понимании это и область (скорее, целый мир) деструктивной интерференции поля. И мы, надеюсь, уже хорошо понимаем, что оттого, что этот Мир ненаблюдаем, он не становится менее реальным, чем видимые фрагменты. Поле в нем по-прежнему живое и динамичное, и, более того, именно эта ненаблюдаемая субстанция объединяет Мир в целое. Мы уже указывали на равенство корней fild (поле) и file (связка).

   Правь для русскоязычного восприятия тоже звучит достаточно прозрачно: закон или — более общо — знание. Подытоживая рассуждения предыдущих глав, мы можем сделать очень простые выводы относительно Прави.

   Напомним:

• стационарные структуры Яви образуются в результате взаимодействия волн совпадающих либо кратных частот;
• движение Яви возникает при наличии слегка несовпадающих частот. Если частотная расстройка велика, Явь распадается;

вращение Яви происходит при изменении фазового сдвига между взаимодействующими волнами.

В этих положениях и заключен Закон, порождающий все многоцветное разнообразие Мира, который управляется удивительно простыми правилами.

Глава 7.

В заключение второго раздела Пропедевтики приведем еще несколько примеров резонансных систем. Мы теперь знаем, что границы ансамбля частиц (иногда невероятно сложные) определяются узловой поверхностью стоячих волн, которые генерируются самим ансамблем. Однако чаще задачу отыскания собственных частот проще рещить на основе анализа конфигурации и размеров поверхности.

Не задаваясь целью детального и количественного описания, отметим некоторые особенности тела человеческого как резонатора. Кстати, детальное описание устройства его и функционирования читатель может найти, например, в «Калагии» А. Наумки- на либо в других эзотерических сочинениях.

Мы вновь отвлечемся от полно- объемного рассмотрения и проана- Рис. 7.1.1. Первая мода лизируем лишь осевые составляю-

щие. Для самой низкочастотной составляющей узловыми точками будут макушка головы и пятки ног.

Пучность стоячей волны приходится на область пупка. Легко определить, что в диапазоне электромагнитных волн с поправкой на диэлектрическую и магнитную проницаемость тканей п = «1,3 соответствующие

где Н = — — 2

скорость света

1 „ Нп^

Собственно магнитогидродинамические волны существенно зависят от напряженности магнитного поля. И хотя волн подобного типа в средах очень много и они

ПЛОХО изучены, но для так называемой альвеновской волны скорость определяется как и = н/Л^ и совпадает с направлением магнитного поля. Для характерной напряженности (Н) магнитного поля Земли 29 ампер на метр, при плотности тканей р ~ 1000 кг/м^ скорость имеет велриину порядка и = 0,26 метра в секунду, достигая в магнитных аномалиях (Н ~ 160 А/м) полутора метров в секунду. Для тела человека, лежащего вдоль меридиана, соответствующие частоты составляют от десятых долей до половины герца, т. е. периоды колебаний от 2 до полутора десятков секунд. В поперечном направлении тела эти частоты могут достигать для рук и ног нескольких герц, для головы — порядка одного герца.

Эти процессы имеют, очевидно, значение при изменении напряженности поля, поскольку изменение скорости волн влечет изменение соответствующего спектра частот, и организм должен подстроиться к нему. Это не всегда безболезненно. Причем, в соответствии с основным голографическим соотнощением AvAx ~ 1, для медленно меняющихся полей, а соответственно, и возбуждаемых частот Av мало, а Ат велико. Здесь, вероятно, кроется причина мучений метеочувствительных людей. При быстром изменении напряженности поля Ат мало, т. е. организм перестраивается очень быстро.

Кроме отмеченной скорости альвеновских волн для сред с плотностью около одного грамма на кубический сантиметр следует обратить внимание на то, что мы находимся в атмосфере, плотность которой всего лишь около 1,3 кг на метр кубический. Соответствующая ей скорость магнитогидродинамических волн составляет величину порядка 7,5 метра в секунду при средней напряженности магнитного пола 29,5 А/м. При определенных условиях магнитогидродинамическая волна обращается в реальное движение воздуха за счет разности давлений, возникающих вслед за скачком магнитной напряженности. Например, если произопшо локальное изменение поля, то в этой локальной области изменится и давление в соответствии с известным соотношением:

б л

Возникает, очевидно, и движение воздуха. Кроме того, изменяется и температура, и плотность воздуха в локальной зоне «скачка» напряженности, связанные с давлением уравнением состояния Р = крТ.

Но это скорее вопросы метеорологии, частично затрагивавшиеся в одной из предыдущих глав. Здесь важнее другое. Если рассматривать парциальные магнитогидродинамические моды для электронной и ионной подсистем жидкости (тканей человека), то помимо уже упомянутых волн со скоростями в четверть метра в секунду мы должны вьщелить еще несколько значимых составляющих. Так, для ионной компоненты, связанной с водородом, возникают волны со скоростью около 0,8 м/с. Но электронная подсистема дает значение скорости альвеновской волны около 15 м/с, что почти вдвое больше упомянутой скорости в воздухе. Из этой близости скоростей вытекают интересные следствия. Первое — опять метеорологического свойства. Энергия движущегося воздуха может переходить в энергию воды. И наоборот. Причем не только за счет механического трения, как обычно считают, но и через посредство магнитного поля.

Что же касается человека, рассматриваемого здесь как резонатор, то из близости скоростей следует, что суще

ствует постоянный механизм обмена энергией с окружающей средой. Причем интересно и то, что для парциальной электронной компоненты со скоростью 15 м/с человек представляет собой резонатор с собственной частотой около 4 Гц. То есть эта частота находится внутри границ низкочастотного «окна прозрачности атмосферы» для электромагнитных волн (7,5^2,5 Гц).

Но вернемся от обсуждения природы стоячих волн в человеке-резонаторе к виду их и влиянию на резонатор. Для второй моды стоячей волны в рассматриваемом одномерном приближении помимо граничных узлов появляется третий в области пупка или чуть ниже него.

Напомним, что для волн с изменением плотности это соответствует тому, что по разные области от узла напряжения имеют всегда противоположное направление и возбуждение второй моды приводит к не очень приятным ощущениям внизу живота.

Одновременно присутствие первой и второй мод вызывает и ощущение внутреннего движения либо вниз, либо вверх, в зависимости от первоначальных значений фаз волн или их разности. Но это не очень выраженное ощущение. Однако если соотношение периодов мод не вполне кратно, то эффект вполне отчетлив. В то же время это означает, что крайние узлы мод не совпадают в пространстве. И если выражение «душевный подъем» или противоположное — «душа ушла в пятки» приемлемо к испытываемому ощущению, то речь, скорее, идет о взаимодействии других мод.

Из рисунка отчетливо видно, что в определенные моменты времени остаются только напряжения, связанные со второй модой и вызывающие неприятные ощущения внизу живота. Третья мода колебаний имеет уже два внутренних узла.

Нижний узел приходится на колени, а верхний — на область солнечного сплетения. Неприятные ощущения, связанные с нижним узлом, известны метеопатам («колени крутит») и наркоманам в период «отходняка». Неприятности верхнего узла хорошо знакомы некоторым студентам во время сессии, а также язвенникам.

Впрочем, причины развития язв и гастритов как раз и кроются в чисто механическом действии третьей моды. Разнонаправленные напряжения травмируют ткани желудка и начала кишечника, и если не принять меры, то травма превращается в область непереносимости агрессивной среды желуцка — гастрит, а затем и нарыв — язву. Конечно же, от качества шггания это зависит весьма мало, и лиып> при наличии травмы диета помогает хоть как-то смирить агрессивность желудочного сок§ и уменьшить страдания. При этом, естественно, возникает некоторый шанс излечения травмы. Как если бы «не сьшать соль на рану».

Возникновение волн высших мод связано с эмоциями и переживаниями, и, в частности, проблемы верхнего узла третьей моды вполне отчетливо связаны с вовремя не потушенным ощущением зависти. Именно завистни- ков-неудачников в народе обзывают язвами, даже если реальной болезни у тех нет. Хотя чаще всего люди не ошибаются, говоря о ком-то: «желчный, язва». Впрочем, чаще всего зависть не объективизируема конкретным имущественным неравенством и носит довольно абстрактный характер. Студент переживает: «Как же так, сокурсники уже все выучили, а я не могу, а экзамен уже завтра». Он, бедолага, даже не подозревает, что проблема в его добросовестности. У «безответственных» сокурсников явный козырь — надежда на авось. Либо билет будет с известной темой, либо удастся списать, а может, экзаменатор пожалеет. И вот здесь возникает продолжение сей печальной истории. Студент, з^иеющий с помощью «авось» или личного обаяния блестяще сдавать экзамены, вдруг обнаруживает, что бывшие середнячки-сокурсники вдруг уже успели защитить диссертации, сделать карьеру, а у него что-то «не клеится». И вот «надежда курса» вместо стихов или прозы начинает писать желчные рецензии и делает это блестяще. Либо выбирает себе поприще сатирика и пародиста. Обратите внимание на желчный цвет лица известных сатириков и их язвительные остроты. Жаль их, бедных. Что-то у них «не срослось», не получилось в жизни. И не смеяться надо над их остротами, а «гнать в шею» с подмостков. Им же лечиться надо, а они здесь страдают. Но это мы отвлеклись. Тема, скорее, для третьей части.

Обратимся к четвертой моде, у которой три внутренних узла. Конечно, нумерацию мод я выбрал неправильно. Первую моду надо бы было назвать нулевой, и тогда номер моды совпадал бы с числом внутренних узлов. Это, наверное, результат невнимательности в студенчестве.

Центральный узел «попадает» в уже известную область низа живота. Нижний находится чуть 1шже колен и проявляет свой негатив иногда в виде судорог либо другим малоизвестным образом. Верхний узел попадает в область груди рядом с сердцем. Это известное в эзотерике лунное сплетение, от которого и страдают, видимо, туберкулезники и инфарктники. Тот же самый механизм. Рвутся ткани. Если сердце, то просто инфаркт. Травмируются легкие — происходит заражение. И опять виноваты эмоции.

Пятая мода—четыре внутренних узла: лодыжки, бедра, пупок, под лунным сплетением. Шестая — верхний внутренний узел в области щитовидной железы. Седьмая — там же (верх горла). Наверняка каждый припомнит ощущения вроде «сдавило горло», «перехватило дыхание».

Читатель, знакомый с эзотерической литературой, уже наверняка сообразил, что узлы «осевой» стоячей волны соответствуют известным чакрам. Тем более что некоторые узлы для разных мод колебаний совпадают и тем усиливают значимость рассматриваемого материала. Интересно исследовать и то, как изменятся частотный спектр и положение узлов при другом положении тела. Например, в случае популярной позы лотоса.

Другим обстоятельством, усложняющим нашу простую схему, является наличие поперечных мод, которые приводят к образованию узловых поверхностей в виде «чаш», «лепестков лотоса» и т. п. Это чрезвычайно интересно само по себе и находится в центре внимания всех школ, исповедующих принцип «познай себя». Но для нас здесь наиболее важно то, что это не досужие вымыслы адептов, а вполне реальные структуры, управляемые эмоциями.

Помимо интегральных частот, свойственных для всего организма в целом, можно выделить и колебания, характерные для отдельных органов, поскольку каждый из них обладает выраженной границей. Сердце человека [диаметром] около одного дециметра, и это сразу приводит к очень важному совпадению. Для скорости магнитогидродинамических (МГД) волн в тканях примерно 0,26 м/с (при обычной напряженности магнитного поля 29 А/м) получаем соответствующую частоту около одного герца, то есть один удар в секунду. Парциальная электронная скорость почти в шестьдесят раз больше, и отсюда возникает еще одна частота, в 60 Гц.

Звуковые колебания распространяются со скоростью примерно 1500 м/с, и для сердечной мышцы появляется еще одна значимая частота в 7500 Гц. Наконец, в электромагнитном диапазоне значимой является частота около 1,2 • 10^ Гц. Однако это не все важнейщие частоты сердца. Для тангенциальных колебаний, распространяющихся по поверхности (длина окружности сердца примерно 30 см), для МГД-волн v ~ 0,3 Гц, а в важнейшем случае трехпетлевой волны v ~ 0,1 Гц и совпадает с частотой первой моды всего организма в положении «сидя» и частотой второй моды в положении «стоя». Отсюда следует, что даже «слегка расшалившиеся» эмоции немедленно начинают «раскачивать» сердце.

Поскольку принципы Природы просты и основаны на кратности частот для стационарных структур, т. е. на универсальной гармоничности, то совершенно не удивительно, что размеры головы человека ровно вдвое больше размеров сердца. Следовательно, «трехпетлевая волна» головы равна росту человека, а это означает, что между резонатором «человек» и резонатором «голова» всегда существуют условия для обмена энергией колебаний. Для тангенциальных, в том числе и трехпетлевых, волн в голове значимо состояние кожи и волосяного покрова, который невероятно усложняет картину колебаний.

Но традиционно считается важнейшей структурой головы кора мозга. Если для сердца длительное напряженное состояние приводит к разрыву мышцы, то то же самое можно отнести и к коре головного мозга. Здесь возможны два исхода. Например, разрыв проходит по кровеносным сосудам, и возникает известная проблема — инсульт. Со всеми последствиями. Другой вариант на первых стадиях развития менее выражен и сопровождается блуждающими головными болями — мигренью. И то не всегда. Но кора мозга растягивается по узловым линиям, и в случаях крайней патологии (при анатомическом уже обследовании) растянутые «швы» узловых линий заполнены не нервной, а соединительной (в данном случае уместнее было бы сказать «разъединительной») тканью. Кора мозга оказывается разделенной на несколько самостоятельных участков, каждый из которых идентифицирует себя как отдельную личность. Речь идет, конечно, о шизофрении. В

детстве, помню, мама рассказывала о жившем в их деревне Ижморке двуглавом молодом человеке. Он прожил немногим более двадцати лет в состоянии чрезвычайного конфликта. Впрочем, говорить о нем в единственном числе неправильно. Все-таки их было двое, и они постоянно ругались между собой. И это неудивительно. Люди, живущие рядом и даже обладающие каждый индивидуальным организмом, нередко собачатся до смертной драки. А тут одно тело и две головы. Один хочет к реке, а другой — в поле. И понеслось! А теперь представьте, что мужичков даже не двое, а больше, но у них и голова-то на всех одна. А внещне вроде бы один человек. Кстати, по оценкам психиатров, картина выглядит вовсе удручающей. До щестидесяти процентов современников имеют признаки шизофрении. Кто в большей, кто в меньшей степени. А причина банальна — все от суеты.

Энергия колебаний, развивающихся в коре, не успевает ни трансформироваться в более высокочастотные структуры (память), ни диссипировать в низкочастотный диапазон. Возникает ситуацрм, аналогичная той, что наблюдается на земной коре. Начинается дробление на фрагменты. Процесс диссипации связан с переносом энергии в моды тела. То есть возбуждение коры в форме интеллектуального напряжения передается в эмоциональную сферу. Возникает чувство либо подавленности и утомления, либо, наоборот, эйфории и «прилива сил». Но представим себе, что эмоций и так «через край», а тут еще и необходимость думать. Такая ситуация характерна для людей творческих профессий, но чаще есть следствие отсутствия культуры и навыков дисциплинированной работы.

Страшнее всего в перспективе развития шизофрении период младенчества, когда интенсивно развиваются соматические структуры мозга. Информационная перегрузка как раз и закладывает основы будущего конфликта. В более позднем возрасте пытаются исправить эти огрехи, но с использованием трудоемких воспитательно-образовательных процедур, а в крайних случаях и путем медикаментозного вмешательства. Но это борьба со следствиями. Причины остаются.

Существует, однако, способ физиотерапевтической профилактики. И выглядит он на первый взгляд довольно несерьезно. Если вокруг головы организовать замкнутый контур и «нагрузить» его на некоторый преобразователь радиочастотного спектра в более жесткий диапазон излучений, то последние будут рассеиваться в пространстве, снимая тем самым напряжение с коры. Ранее мы обсуждали возможность генерации жестких излучений при низкочастотной накачке. Так, например, радиочастотный спектр 10’ Гц может быть инвертирован в импульсы рентгеновского диапазона 10’’ Гц. Если «излучатель» собран из дисперсной системы произвольно ориентированных кристалликов, то рассеяние будет изотропным (равномерным по всем направлениям) и ввиду малой интенсивности вреда не принесет. Требования к материалу контура практически отсутствуют, потому как речь идет о тангенциальных колебаниях, и индуцированное поле будет представлено в основном поверхностными плазмонами, для которых проводимость значения не имеет (см. гл. 5). То есть можно использовать тряпичный, бумажный, кожаный или даже берестяной ободок с кармашком для песка, соли или толченого кирпича.

Что удивительно, так это то, что сей эффективный физиотерапевтический прием известен хорошо нашим бабушкам и дедушкам с древнейших времен. Наши бабушки для снятия головной боли брали платок или салфетку, насыпали в центр ложку соли или песка, скручивали платок в жгут и повязывали вокруг головы. Очень скоро боль отступает. Не верите? Проверьте сами. Но традиция носить обереги уходит в седую древность. Оттуда же пришла и фуражка с кокардой из мелкокристаллических материалов.

Кстати, следует обратить внимание на то, что можно в качестве преобразователя использовать и качественные природные или синтетические кристаллы. Но поскольку они излучают лишь в нескольких определенных направлениях и очень узкими пучками, то польза от них может обернуться бедой. Локальное поражение тканей может привести к трагическому исходу. Здесь уместно вспомнить о трагических судьбах обладателей больших драгоценных камней. Как правило, эти камни в оправе (контур) со строгой геометрией (отражающие поверхности) носились на подвеске на груди. Подвеска (металлическая цепь или шелковая нить — неважно) тоже является контуром. Камень на одном месте и в одном и том же положении. Можно вместо такого генератора и обычной спицей воспользоваться.

Обратимся теперь к радиочастотному диапазону нашего тела-резонатора. Это около одного гигагерца ~ 10’ Гц. Можно сразу возразить, что никто этих излучений от человека не обнаружил. Но, возразим, именно в этом диапазоне работают медицинские приборы на основе ядерного резонанса. Конечно, речь идет не об этом. Дело в том, что в норме мы и не должны обнаруживать никакого излучения. Точно так же как в опытах с интерференцией света. В области конструктивной интерференции мы его обнаруживаем, а там, где деструктивная интерференция, там нет его. Но волны как бежали, так и бегут. Просто исправно в этом месте гасят друг друга.

Вспомним, что и сам человек есть не что иное, как (очень сложная) область конструктивной интерференции. Можно, впрочем, рассуждать и по-иному. Устойчивость голографической картинки обеспечивается совпадением либо кратностью частот волнового ансамбля. Для простой системы, полученной интерференцией ограниченного числа волн, это условие выполняется только при наличии достаточно мощных источников качественного (когерентного) излучения. Но для более сложной системы возникают условия самосинхронизации в виде упоминавшегося ранее макрокинетическо- го принципа: система высшего порядка стабилизирует нижестоящие. Физический смысл этого положения достаточно прост и очевиден. Действие системы высшего уровня с некоторой средней для всего ансамбля частотой является вынуждающей силой, которая и «подтягивает» частоты «элементарных» осцршляторов нижестоящих участников процесса к этой средней частоте. В данном случае средней частотой может оказаться не полусумма двух, например, частот, а их разность. Впрочем, с формальной точки зрения это то же самое, но в частотном или энергетическом отношении означает, что поведением «высокоэнергичных» участников ансамбля управляют низкоэнергетические процессы. Для любителей математических упражнений в этом месте следовало бы привести соответствующие случаю фор

мулы, но это достаточно элементарные примеры сложения синусов-косинусов из школьной тригонометрии, и мы не будем этого делать.

Из этих достаточно строгих формально-формульных выводов (трудно удержаться от очередного каламбура) следуют многие фундаментальные результаты, применимые к системам самого разного иерархического уровня. Чем ближе собственные частоты взаимодействующих объектов (или субъектов), тем ниже их управ- ляюще-результирующая частота. Это обстоятельство для ансамбля химических элементов мы уже обсуждали в предыдущих главах. Здесь же в качестве шутки вспомним поведение пары собеседников. Если они малознакомы, то взаимодействие почти отсутствует. Уж очень разные собственные частоты. По мере сближения частоты подтягиваются к средней, и возникает довольно болтливая компания. Болтовня — это, несомненно, низкочастотный обмен на соответствующей разностной частоте. Теперь вообразим: беседа затянулась на месяцы и годы. Сотрудничество или супружество — неважно. Собственные частоты почти совпали и равняются средней, естественно, а разностная становится очень низкой. И хотя это уже прочная «ячейка общества», активно сотрудничающая и между собой (внутри себя), но словесный обмен становится скорее исключением, чем обыденным правилом. Наверняка наблюдательный читатель обращал внимание на такие совпадения. Только хочешь что-нибудь подсказать родственнику или другу, а он говорит или делает то же самое. Иногда возникает даже некоторая ревность или раздражение. «Друзья любят поговорить молча». И это уже не шутка. Дело в том, что давние партнеры общаются между собой не на разностной частоте, а на средней, которая у них те- перь совпадает с их собственными. Резонанс. Или — более высокопарно — гармония душ. И это в любом случае довольно высокие частоты. Для альвеновских волн — порядка 60 Гц, для магнитозвуковых — примерно 7500 Гц и для электромагнитных — около миллиарда герц. Известные из биологии скорости распространения нервных импульсов (около 70 метров в секунду) дают частоты для коры головного мозга порядка 100 Гц, что очень близко к альвеновским модам.

Поскольку даже в случае электромагнитных колебаний мы имеем дело не с классическими бегущими волнами, а со структурой из них, то генерируемые излучения могут иметь и продольные компоненты с еще более высокими скоростями. Например, по оценке Ацюковского, это величина порядка 10^’ м/с. Соответствующие частоты для резонатора с размером около двух метров (человек) обладают невероятно большими значениями — около 1Гц. Возможность генерации частот этого диапазона обсуждалась нами ранее в несколько ином ключе, как следствие резонанса в ансамбле из очень большого числа частиц, возбуждаемого радиочастотным излучением. Столь высокие частоты соответствуют энергиям поля, способного рождать протоны. Но не это важно. Если словесное общение происходит с частотами до ста слов-образов в минуту, то следует сделать вывод, что примерно такое же количество образов мы можем воспринимать и по другим каналам. Отсюда следуют некоторые оценки для расстояний, на которых могут общаться телепатирующие собеседники. Если обмен следует с частотой около одного герца (положим для

Простоты), то для альвеновских мод (скорость в воздухе ~ 7,5 м/с) это, соответственно, расстояние порядка 7,5 метра, для звуковых и магнитозвуковых — порядка 350 м (можно, конечно, и погромче крикнуть, но сложно). Для электромагнитных — около 300 000 километров (напомним, что длина земного экватора — всего 40 000 км). И, наконец, для продольных электромагнитных волн — порядка 10^’ метров. Это, конечно, фантастика. Но кто знает все?

Для сравнения приведем примерный размер нашей Галактики в поперечнике. Поскольку наша Солнечная система находится на периферии и движется со скоростью около 230 км/с, совершая оборот вокруг галактического центра за время порядка 180 миллионов лет, то оценка поперечника дает величину около 1,3 • 10^’ метра. Вот те на!

МУШТРА И КАМЛАНИЕ

Мы обсудили человеческий организм в смысле его резонансных свойств. И даже рассмотрели взаимодействие двух партнеров. А что, если человек один или если их (человеков) много.

Для посвятившего свою жизнь внутреннему самосозерцанию (опять каламбур), то есть йогу, главное (чуть ли не цель жизни) — это прекращение внутреннего диалога. Словесно-образное (читай по-нашему, логическое) мышление должно уступить место образному (то бишь иррациональному) мышлению. Главное условие на этом пути состоит в том, чтобы словесное мышление вовсе исчезло.

Возвращаясь к частотным соображениям (это опять каламбур), мы должны сообразить, что словесный диалог (сам собой) прекратился и «обратились мы» к «чистым» образам. К этому набору каламбурных сочетаний мы должны, несомненно, добавить термин «образование». Но довольно каламбуров, перейдем к сути.

Йог, в некоторых извращенных языках читаемый «сзаду наперед» — Гой, в своей практике медитаций уподобляет себя бессмысленному ничтожеству. Он перестает думать. И вот здесь возникает ситуация не то чтобы бессмысленная, но, по крайней мере, двусмысленная. Он, йог, представляет собой любой набор ансамблевых частот, пришедших в гармонию. Он находится теперь только под влиянием самых низших (хорошо бы сказать, нупевых) разностных частот и по «средней» частоте сопереживает со всем Миром. А теперь вспомним скорость «сопереживания», которая в пределах Галактики есть обычная «скорость» эмоций человека.

Но йоги — это йоги. Мы — простые смертные. И у нас простые задачи. Но решение множества проблем гораздо легче осушествляется коллективным трудом. Да и само развитие человеческого вида есть кооперативный процесс. Каким образом достигается гармония в человеческих ансамблях? Рассмотрим некоторые простейшие случаи. Например, воинское подразделение. Взвод, роту или батальон. В тот момент, когда решаются задачи, ради которых и создаются подобные формирования, как правило, нет времени для объяснений, согласований и выработки общего мнения. Поэтому боевая дружина должна функционировать как единый организм с единым «мозгом». И практика войн представляет убедительные примеры подобного рода.

Мы теперь уже знаем, что для этого нужно «подтянуть» индивидуальные частоты как можно ближе к некоей средней. И можно сделать это не в высокочастотном диапазоне, а в более удобном, физиологическом или психоэмоциональном. Естественно, задав некоторый общий ритм вблизи любого известного. Например, на частоте сокращения сердечной мышцы. Поэтому бесконечное хождение строем по плацу под ритмичные звуки барабана — занятие не такое уж и бессмысленное, как кажется на первый взгляд. Эффект усиливается при наличии флейты или оркестра. Причем соверщенно не важно, исполняют они красивую мелодию марша или просто взвизгивают под ритм того же барабана. Но, как правило, используются короткие музыкальные фразы, повторяющиеся с частотой в несколько десятых долей герца.

Вспомним, сержант, исполняющий функцию барабана, командует отделению: раз, два, три,…, раз, два, три. «Четыре» он уже не произносит. В этом слове целых три слога и они уже не вписываются в ритм. Вместо «четыре» следует пауза. Иногда используется команда без паузы: три, четыре — три, четыре. Ритм опять в четыре слога. Естественно, для «сбивки» коллектива важны и еще более низкочастотные ритмы. И с периодом в десятки секунд, и то, что называется распорядком дня.

Использование низкочастотных ритмов эффективно не только для армейских коллективов. Из этой же обоймы и африканские традиции работы под звуки тамтама и тому подобное.

Культовые обряды с ритмическими песнопениями и танцами мы теперь также можем объяснить как процесс гармонизации (настройки) общины или племени. Несколько иной смысл, чем при медитации у йогов, вероятно, заложен в камлании шаманов. Делается это принародно, и, скорее всего, шаман использует коллективное заторможенное (или, может, точнее будет сказать — чистое) сознание с целью совершения какого-либо действия или для получения той или иной информации.

Во всех этих ритуалах есть очень много схожего, и хотя мы уже почти «влезли» в эзотерику, я думаю, что это не очень смущает читателя. Должно же и этим аспектам нашей жизни находить рациональное объяснение.

Особо следует подчеркнуть, что в большинстве способов гармонизации используются некоторые технические средства: бубен, барабан, оркестр и так далее. Именно о технической стороне вопроса пойдет речь в следующем параграфе.

ХРАМ

ЧЕЛОВЕК

частоты имеют порядок — = Т

. V с

высота человека; А, — длина волны; с – в вакууме, откуда v ~ 6,4 • 10’ Гц. Это очень быстрый процесс. Однако для плотных сред более значимыми являются звуковые и магнитогидродинамические колебания. Последние очень часто имеют скорости соответствующих волн вблизи звуковой. Полагая, что ткани человеческие не слишком отличаются от воды и жиров, примем соответствующую скорость за 1500 метров в секунду. Тогда 400 Гц или чуть больще. Это тоже достаточно быстрый процесс и в реальной жизни имеет, как и предыдущий электромагнитный, мало места вследствие значительного затухания. В противном случае мы, вероятно, должны были бы слышать этот звук баритонального или свистящего для кратных частот характера. Обычно это наблюдается в патологии. Довольно часто можно услышать гудение в одном ухе. В этом случае люди шутят, спрашивая у соседей: «В каком ухе звенит?» Но иногда, как, например, у автора, это постоянное звуковое «сопровождение». Проблема заключается в расстройке компенсаторных систем нервной системы.

Р2-Р|=-^(Н2-Н^).

Рис. 7.1.2. Вторая мода

Рис. 7.1.3. Взаимодействие двух первичных мод

Рис. 7.1.4. Третья мода колебаний

Рис. 7.1.5. Четвертая мода

Рис. 7.1.6. Поза лотоса и первая мода

Теперь нижний граничный узел для всех мод можно считать находящимся у крестца или копчика, где расположена главная сакральная чакра и «свернут» змей Кундалини. Частоты мод при прежней скорости распространения магнитогидродинамических волн для позы лотоса практически вдвое выше, чем для положения «стоя». Это означает, что, например, парциальная электронная частота оказывается вблизи важнейшей физиологической частоты 7,5 Гц.

Узел второй моды позы лотоса приходится на область груди (лунное сплетение). Третьей — на яремную впадину (щитовидная железа) и желудок (солнечное сплетение). Четвертая мода имеет узлы в области головы, на

уровне мозжечка, лунного сплетения и пупка. И пятая мода с узлами в области гипофиза, верхней части груди, в области солнечного сплетения и чуть ниже пупка.

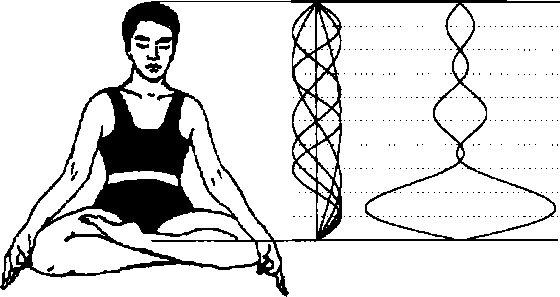
Рис. 7.1.7. Узлы первых пяти мод для позы лотоса

Рассмотренные схемы узлов, конечно, условны, так как в реальности надо рассматривать суммарные колебания, и здесь многое зависит от первоначальных фаз мод. Например, сумма первых трех мод при одинаковых начальных фазах выглядит следующим образом.

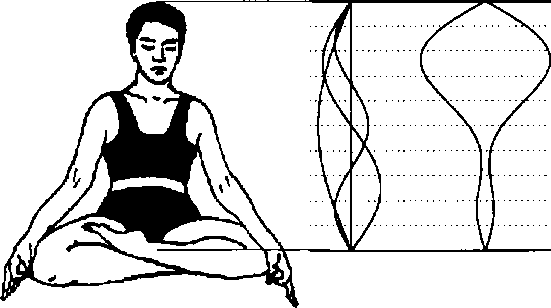
Рис. 7.1.8. Пример с другим первоначальным распределением фаз

ЦЕРКОВЬ

Слово «храм», вероятно, родственно понятию «хоромы», и оба происходят от слов «краска, красить, красивый». Замена «к^х» здесь вполне естественна. Впрочем, этот корень слова мы уже рассматривали в первой части и прищли к выводу, что «красиво» и «хорошо» — это почти одно и то же. Можно вспомнить еще и название химического элемента — хром. Нетрудно сообразить, что связано оно с чудесными теплыми тонами зеленого цвета, характерными для красок на основе солей этого элемента.

Что ж, несомненно, большинство культовых сооружений красивы и радуют глаз не только раскраской, но и гармонией пропорций. Это последнее обстоятельство для нас особенно важно, ибо оно и составляет предмет нашего интереса. Теперь-то мы хорошо знаем, что за геометрической гармонией стоит и гармония динами- ческая. Гармония звуков, электромагнитных колебаний и так далее. А в храм идут за гармонией души. Идут и тем самым оживляют и сам храм.

В церкви не всегда стояли. Да и до сих пор у многих народов культовые обряды необязательно связаны с каким-либо сооружением. Но, собравшись в круг, люди воздают хвалу обожествляемым пращурам своими песнями и хороводами. Конечно, и в надежде на защиту и покровительство. Но это частность. Этимология слова «церковь» — в понятии «цирк — круг». Но одновременно это и динамическое понятие движения по замкнутому контуру (иногда по кругу) — циркуляция. Понятие «собор» происходит от живого глагола «собираться в круг (цирк)». Собирать корни слов — для автора любимое занятие, и напомню, что в «пакете собор» мы уже отмечали белорусское сябры — друзья, народ сербы, край Сибирь и многое другое.

Рассуждая о культовых обрядах и сооружениях, необходимо пояснить и этимологию самого термина «культ». Он явным образом перекликается со словом «хулить». В современном языке это означает «ругать». Но вряд ли было ругательством. Это достаточно обычная инверсия смысла и в истории языков наблюдается довольно часто. Например, в восточнославянских языках ласковое «урода» — красавица или, точнее, божественная — обращается в современном русском (?) в соверщенно противоположный смысл — безобразного. Хулить, по смыслу прежнему, было понятием «хвалить, славить». Но когда вместо хвалебного поминания богов — предков (а вспомните, что и ныне: «о мертвых либо хорошо, либо ничего») у них начинают даже не помощи просить, а просто попрошайничать, то у нищих этих понятие «хвалить» становится ругательством. И начинают они хулить и жизнь свою, и предков, и все вокруг. Но это проблемы этики. И тем не менее эта инверсия смысла термина «хваления» лишний раз показывает древность понятия «православие». Ибо не просить, а лишь поминать с любовью.

Однако пора вернуться к физическому смыслу гармонии культовых сооружений. Церкви и мечети строятся по жестким канонам, и все пропорции, и элементы несут вполне определенный смысл. Основное сооружение представляет собой куб и с точки зрения частотных и волновых свойств является резонатором для трех ортогональных колебаний с одинаковой частотой. Если допустить, что какой-то элемент строения осуществляет функцию фазовращателя, то образующаяся узловая поверхность объемной стоячей волны совпадает с поверхностью щара и очень близка к поверхности полярного тора.

Сторона куба разных церквей неодинакова, но, как правило, это около 18-^20 метров. Учитывая, что скорость звука в воздухе около 340 м/с, получаем частоту основной моды колебаний в храме порядка 17-^20 Гц. Это низкочастотная граница диапазона частот, доступных восприятию человеческого уха. По музыкальной классификации такие частоты следует классифицировать, вероятно, как гиперконтрабасовые. Возбудить такой резонатор непосредственно человеческим голосом достаточно трудно. На каждой стене храма есть по три равномерно расположенных проема — окна или двери.

Поэтому звуки, образующие вдоль стен стоячие волны, должны иметь утроенные по сравнению с основной модой частоты, поскольку резонно полагать, что их узлы не могут находиться в проемах. Проемы более пррш)дны для пучностей. Условно это можно изобразить следующим образом.

На самом деле «конфигурация» стоячей волны вдоль стен храма гораздо сложнее. И, скорее всего, назначение проемов и простенков состоит в преобразовании частот. Утроенная основная мода — это уже нормальный басовый диапазон 51-^60 Гц, доступный низкому голосу.

Высота проемов, как правило, не достигает половины высоты куба, поскольку в центре каждой грани находится узел основной моды резонатора, и там, естественно, не должно быть проема.

Основное строение перекрыто куполом, чуть ниже которого располагается балкон для хористов, поющих высокими голосами. В центре купола сквозной круглый проем, сопряженный с полым цилиндром. Цилиндр, в свою очередь, накрыт «луковицей» овершения. Поскольку мы имеем дело явно с резонансной системой, то нетрудно угадать в луковице резонатор Гельмгольца, концентрирующий в свой «хвост» энергию звуков, произносимых в храме. «Хвост» резонатора Гельмгольца заканчивается подкрестовым яблоком, на которое, естественно, устанавливается сам крест. Крест, как и все сооружение, строго ориентирован по сторонам света и своей плоскостью «смотрит» на восток. Если теперь отнять у владыки державу и поставить ее в подкрестовое яблоко, то получится довольно высоковольтный генератор переменного напряжения.

Держава выполнялась из горного хрусталя (пьезокварц) высокого качества. По экватору державу охватывает металлическое (проводящее) кольцо, а в отверстие по полярной оси вставляется металлический стержень, заканчивающийся крестиком.

По сути дела, держава — это довольно простой пьезоэлектрический звукосниматель. В <осво- сте» резонатора Гельмгольца при поющем храме развивается большое звуковое давление, и такой «простой» звукосниматель способен развивать на своих электродах (кольцо и стержень) разность потенциалов в несколько десятков тысяч вольт.

Крест, если он выполнен, например, из сухой древесины и с двух сторон имеет металлизированное покрытие, представляет собой не что иное, как конденсатор. Можно вообразить и несколько более сложную конструкцию конденсатора из трех обкладок. Такой крест легче соединить с пьезоэлектрическим генератором в форме державы. Например, центральную обкладку соединяя с крестиком, а наружные — с кольцом. Можно довольно просто показать, что крест в этом случае становится антенной, излучающей электромагнитное поле звуковых частот. Но интересно не это. Если диэлектрик (древесину) креста-конденсатора наделить, например, сегнетоэлектрическими свойствами, то крест превращается в широкополосный генератор высокочастотных колебаний. Это тоже легко показать. Диэлектрическая проницаемость диэлектрика (е) зависит от напряженности электрического поля. Причем для некоторых сегне- тоэлектриков очень сильно.

Напомним теперь, что резонансные частоты для частиц вещества, в свою очередь, зависят от диэлектрической проницаемости:

Изменение структуры означает изменение конфигурации объемных стоячих волн, при этом, как и в случае опыта с двумя зеркалами, в излучаемых волнах возникает продольная составляющая. Со всеми последствиями, включая возможность связи в реальном времени с очень отдаленными партнерами. Дело еще и в том, что описанная конструкция может работать как в режиме передачи, так и в режиме приема. Если сегнетоэлек- трический крест окажется в поле излучения такого же креста, то интегральное частотное воздействие должно приводить к изменению структуры и, соответственно, диэлектрической проницаемости. На обкладках появится напряжение звуковой частоты, а пьезоэлектрическая держава должна зазвучать.

Вообще, православная церковь, правильно оборудованная, есть не что иное, как банальный телефон. Стучат в колокола — вызов на связь. Потом начинают общаться. Вопрос — с кем?

Продолжим наше фантастическое исследование культовых сооружений. Мусульманские мечети по овер- шию иногда повторяют православные церкви, но чаще накрыты полусферическим куполом. Вместо колоколен рядом с мечетью стоит один, а иногда несколько минаретов. Минареты по форме своей очень узнаваемы, поскольку сильно смахивают на современные ракеты. И очень похожи на ступы (тоже культовые сооружения) юго-востока Азии.

Про ступу Бабы-яги мы все помним с детства. С помощью ступы и помела Баба-яга перемещалась в пространстве. Если ступа бабушкина была похожа на камбоджийскую или на минарет, то тогда и с помелом все ясно. Это точнейший образ современной ракеты. А мечеть — естественно, образ комплекса связи и управления полетом. Достаточно взглянуть на аналогичные сооружения вблизи любого практически аэродрома. Да и само слово «мечеть», несомненно, созвучно слову «метать». Сегодня мы говорим: пусковой комплекс. А можно было бы говорить: метательный.

Надеюсь, что технизация церквей и мечетей нисколько не умаляет их культового значения. Аминь.

Что касается храма—как дома Господа, то Иоанн-бо- гослов в откровении, описывая небесный город — Новый Иерусалим, говорит: «Храма же я не видел в нем: ибо Господь Бог Вседержитель — храм его и Агнец». (Синодальное издание, Москва, 1991 г.)

ЗАКЛЮЧЕНИЕ

Вариант описания реальности, предложенный данным сочинением, основывается на теории волн и колебаний. Конечно же, невозможно себе представить, что это исчерпывающий вариант. Множество деталей требует доработки, но и в целом это всего лишь вариант. Возможны и другие, ибо каждый творит свою Вселенную сам. Но в любом случае, читатель, прими мою искреннюю благодарность за труд. Без твоего терпеливого участия я не смог бы одолеть эту длинную, но радостную дорогу.

Рис. 7.3.1. План основного строения храма

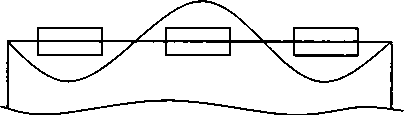
Рис. 7.3.2. Стоячая волна вдоль стены храма

Рис. 7.3.3. Держава, скипетр, шапка

Рис. 7.3.4. Держава в разрезе (предположительно)

4WV /УУУ4

\\\V

\\\V

\\\\’

\\\V /УАУ, \\\V \\\V \\\V

4WV ///л \\\V /у А/, 4WV УУУЛ 4WV /УУ/i

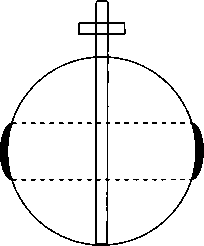
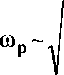
2 2 е Z п

8овт

Здесь, как и прежде, е — элементарный заряд, Z — число зарядов иона, п — концентрация ионов, е,, — электрическая постоянная, ш — масса иона. При изменении 8 соответственным образом меняются резонансные частоты всех компонент вещества, то есть для всех сортов частиц, включая электроны, ионы и более сложные структуры. Поскольку собственная энергия каждой частицы непосредственно зависит от частоты колебаний

Е ~ mAW,

здесь А — амплитуда колебаний, то при изменении частоты частица будет либо излучать, либо принимать энергию. А так как в любом материале очень много сортов частиц, то и излучение будет очень широкополосным, но, естественно, промодулированным исходными звуковыми частотами. И это еще не все. С изменением резонансных частот вещество должно испытывать структурную перестройку, поскольку нарушается исходное состояние, возникшее из условия кратности частот, и должно возникнуть новое, вновь удовлетворяющее тому же условию. Впрочем, это и есть причина изменения диэлектрической проницаемости.

ГОЛОГРАФИЯ ВСЕЛЕННОЙ

ГЕОМЕТРИЯ ПРОСТРАНСТВА И ВРЕМЕНИ

Ответственный редактор С. Ключников Дизайн и верстка Р. Рагимов Корректор Т. Чернова

Издательская лицензия ЛР № 066606 от 19.05.99 Формат 84×108/32. Бумага офсетная. Печать офсетная. Гарнитура Times New Roman.

10,85 печ. л. Тираж 1000 экз. Зак. № 1360.

 

Тел.: +7 (903) 707-92-23 E-mail: belovodje@rambler.ru

Отпечатано в полном соответствии с качеством предоставленных материалов в ООО «Производственная фирма «Полиграф-Периодика» 160001, г. Вологда, ул. Челюскинцев, д. 3