В первый раз продемонстрирована хаотическая динамика популяций в многовидовом сообществе

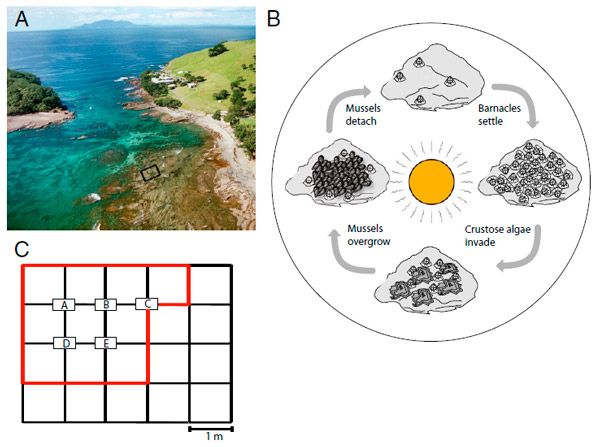
Рис. 1. Сообщество скалистой приливно-отливной территории. А — вид с воздуха на место проведения изучений.

В — схема циклической сукцессии. С — схема экспериментальной площадки, складывавшейся из двадцати участков и пяти узлов (отмечены буквами). Процент площади, занятой обнажёнными камнями, корковыми водорослями и морскими уточками, наблюдался на участках, а покров мидий оценивался по фотографиям узлов.

В анализе временных последовательностей употреблялись эти, полученные на десяти выделенных участках и во всех пяти узлах. Рисунок из обсуждаемой статьи в PNAS

Достаточно давно было предсказано, что вмноговидовых сообществах может появляться хаотическое поведение. Но примеров «из природы» не было известно, не в последнюю очередь из-за трудности доказательства хаотического характера поведения. Двадцатилетние наблюдения за тремя видами, заселяющими камни в приливно-отливной территории на побережье Новой Зеландии, продемонстрировали, что эта экосистема находится «на краю хаоса»: иногда динамика численностей изменяется со стабилизирующейся на хаотическую.

Одно из значимых открытий в математике XX века — это динамический, либо детерминированный, хаос. Не смотря на то, что родные идеи изучались еще в финише XIX века в работах французских математиков Анри Пуанкаре и Жака Адамара, основоположником теории хаоса вычисляют метеоролога Эдварда и американского математика Лоренца. Мысль хаотического, принципиально непредсказуемого поведения совокупностей, порожденных строго детерминированными (и достаточно несложными) уравнениями, взбудоражила головы многих философов и учёных (краткую современное исследования состояние и историю хаоса неприятности возможно отыскать в обзорной статье A. E. Motter, D. K. Campbell, 2013. Chaos at fifty). Но, за время от времени неумеренно восторженными славословиями хаосу как «новой парадигме» может теряться настоящее использование этих идей для описания окружающего мира.

А они бессчётны, в том числе и в биологии (см., к примеру, статью M. Doebeli, I. Ispolatov, 2014. Chaos and unpredictability in evolution и маленькую видеолекцию одного из авторов данной статьи).

Что такое хаос

Нерегулярность и следующую из нее непредсказуемость, характерные природным явлениям, традиционно растолковывали действием случайных факторов, каковые сбивают совокупность с поведения, предписанного внутренними законами. Но оказалось, что смогут существовать и такие совокупности, каковые развиваются строго детерминированно, не отклоняясь от предписаний уравнений, обрисовывающих их динамику, но смотреться это будет так, словно бы ведут они себя совсем случайно. Такая совокупность может какое количество угодно раз возвращаться к уже существовавшим состояниям, но любой раз затем будет вести себя по-второму.

Как так возможно? Так как использование одного и того же уравнения к одним и тем же значениям (мы говорим, что совокупность «возвратилась» в прошлое состояние) должно давать одинаковые результаты? Дело в том, что совокупность возвращается не строго в то же состояние, а в близкое к нему (так близкое, что мы не сможем измерить эту отличие). Наряду с этим уравнения устроены так, что малые различия со временем не затухают, а усиливаются (нужным, но не достаточным условием для этого есть нелинейная связь между переменными).

Исходя из этого нам и думается, что совокупность ведет себя, не подчиняясь никаким законам.

На рисунке приведены типы популяционной динамики, появляющиеся в модели Ферхюльста. На графике «г» изображен четырехточечный цикл. Он выглядит сложно, но поведение совокупности предсказуемо: по окончании максимального значения численности будет минимально вероятное, по окончании него — второе по величине, позже — третье, и — снова максимум. Зная численность популяции в один из годов, мы сможем совершенно верно заявить, что с нею будет дальше.

На графиках «д» и «е» изображены хаотические колебания. Тут за пиком может направляться различное: то ли один пик мельче, то ли два пика — зная численность популяции в этот год, мы не сможем заявить, что ее ожидает дальше. Еще раз выделим: это не связано с какими-то действиями на совокупность, это — ее личная, внутренняя динамика.

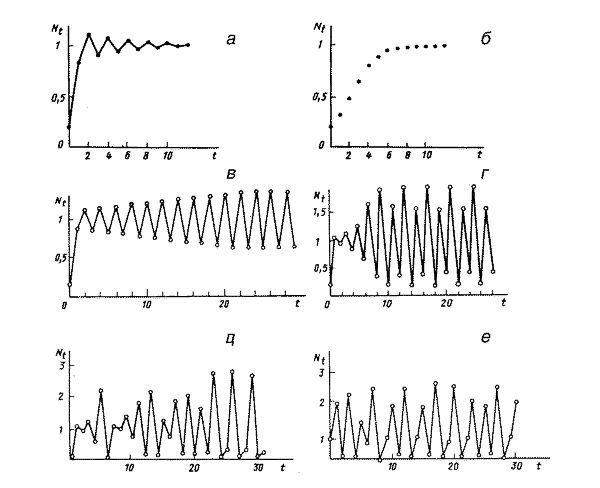
Типы динамики численности в модели популяции с неперекрывающимися поколениями в ограниченной среде при различных значениях собственной скорости роста. а — затухающие колебания; б — монотонный рост с выходом на плато (данный вариант — единственно вероятный в соответствующей модели с перекрывающимися поколениями); в — двухточечный цикл; г — четырехточечный цикл; д, е — квазистохастическое (хаотическое) поведение. Рисунок из книги Г. Ю. Ризниченко «Математическое моделирование»

В экологии хаос появляется в математических моделях, обрисовывающих динамику отдельных сообществ и популяций. Он может порождаться кроме того несложной моделью Ферхюльста, обрисовывающей рост популяции в ограниченной среде, при условии наличия дискретных, неперекрывающихся поколений. Подтверждения существования хаотической динамики приходили кроме этого из лабораторных опытов над популяциями насекомых (R. F. Costantino et al., 1997.

Chaotic dynamics in an insect population), микробными пищевыми сетями (L. Becks et al., 2005. Experimental demonstration of chaos in a microbial food web) и планктоном (E. Benincà et al., 2008. Chaos in a long-term experiment with a plankton community).

Наблюдения хаоса в природе редки, и в главном ограничены наблюдениями за динамикой отдельной популяции (P. Turchin, S. P. Ellner, 2000. Living on the edge of chaos: Population dynamics of Fennoscandian voles). Но, это не должно быть трактовано как уникальность хаотической динамики: ее очень сложно найти, поскольку снаружи похожее поведение может появляться и за счет не детерминированных процессов, а стохастических (случайных) действий, нарушающих закономерное развитие экосистем. Но в последние годы показались математические способы, разрешающие обнаруживать хаотическое поведение кроме того в присутствии внешнего шума (см., к примеру, книгу P. Turchin, 2003.

Complex Population Dynamics: A Theoretical/Empirical Synthesis).

И вот интернациональной группе исследователей удалось найти хаотическое поведение в циклической сукцессии в сообществе каменистой приливно-отливной территории в морском заповеднике «Мыс Родни — мыс Окакари» (Cape Rodney-Okakari Point Marine Reserve) на Северном острове Новой Зеландии. Сукцессией именуют воспроизводимый процесс смены сообществ, где одно в буквальном смысле «готовит землю» для другого. Обычный пример из школьного книжки — восстановление ельника по окончании пожара, начинающееся с травяных сообществ и проходящее через пара кустарниковых и лесных стадий.

В большинстве случаев сукцессии линейны — от пионерных (начальных) стадий через сериальные (промежуточные) к климаксной (финальной). Климаксное сообщество отличается тем, что способно устойчиво воспроизводиться (оно «готовит землю» лишь для себя самого). Но в некоторых случаях климаксное сообщество неустойчиво и снова сменяется пионерным, тем самым возвращая экосистему в начало процесса — в таком случае говорят о циклической сукцессии.

Они видятся в экосистемах с нередкими эндогенными пожарами (к примеру, чапараль): неизбежное выгорание климаксного сообщества делает сукцессию циклической.

Подобная обстановка отмечается и на камнях приливно-отливной территории изученного морского заповедника (рис. 1, В). Обнажённые камни массово заселяются морскими уточками Chamaesipho columna (ракообразные, живущие в домиках, прикрепленных к жёсткому субстрату). Поверх морских уточек увеличиваются корковые бурые водоросли Ralfsia cf. confusa. На уточек и водоросли заселяются мидии Xenostrobus pulex, неспособные колонизировать обнажённые камни. Но, в отличие от водорослей, мидии «не заботятся» о собственных соседях, и под их прессом морские уточки погибают.

Погибшие ракообразные и водоросли открепляются от субстрата и уносятся отливами и приливами, а вместе с ними — и мидии. И в итоге мы имеем те же обнажённые камни, с которых всё началось: экосистема готова к новому циклу.

Исходными данными для работы стали результаты двадцатилетних наблюдений: каждые тридцать дней исследователи собирали информацию о площади камней, занятых каждым из трех видов, и свободных от визитёров на большой умелой площадке (рис. 1, С). Необходимо подчеркнуть, что в этом случае наличие в экосистеме циклической сукцессии не обязано приводить и к цикличности в численностях популяций: не смотря на то, что на каждом отдельном камне происходят колебания численности, на всем пространстве смогут установиться некие средние значения. Но в данном случае для того чтобы не случилось (рис. 2).

Авторы делятся собственными впечатлениями: «В кое-какие годы камни были полностью покрыты морскими уточками, в то время как в другие — корковые водоросли либо мидии господствовали в экосистеме» (как говорится, год на год не приходится). Вейвлет-анализ (см. Н. М. Астафьева, 1996. «Вейвлет-примеры: основы применения и анализ теории») взятых временных последовательностей распознал приблизительно двухлетнюю периодичность в динамике всех пар видов. Морским уточкам требуется от полугода до года, дабы заселить камни, с отставанием в пара месяцев за ними следуют корковые водоросли.

Мидиям кроме этого требуется 6–12 месяцев, дабы образовать плотный покров на домиках ракообразных, и еще приблизительно полгода проходит от доминирования мидий до обнажённых камней, готовых к заселению морскими уточками.

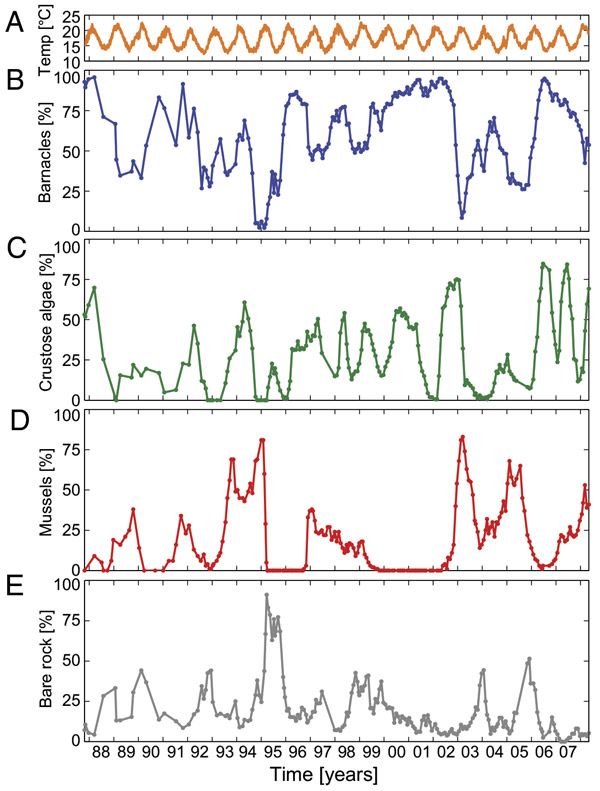
Рис. 2. Зарегистрированная динамика трансформации по времени (в годах): температуры (А) и площади, занятой морскими уточками (В), корковыми водорослями (С), мидиями (D), обнажёнными камнями (Е). Рисунок из обсуждаемой статьи в PNAS

Но, найденные периоды не выдерживаются строго: колебания видового состава сообщества были очень нерегулярны. Тут-то и прячется хаос. Авторы изучения оценили ляпуновские показатели (Lyapunov exponent), характеризующие скорости сближения либо удаления двух родных фазовых траекторий (траекторий в фазовом пространстве совокупности, где любая точка является состоянием совокупности, а координатами являются параметры, обрисовывающие совокупность; в данном случае параметрами являлись площади камней, занятые различными видами). Наличие хороших ляпуновских показателей показывает, что исходно малая отличие между траекториями со временем экспоненциально увеличивается и траектории расходятся — это есть показателем хаотического поведения; отрицательные же, напротив, показывают, что существующие различия со временем сглаживаются — траектории сближаются. Глобальный ляпуновский показатель, оцененный по всем двадцати годам наблюдений, был хорошим: +1,1 год–1.

Но его отличие от нуля выяснилось незначимым. Но локальные ляпуновские показатели, оцененные по периодам в 180 дней, существенно колебались, довольно часто выясняясь значительно выше нуля (рис. 3).

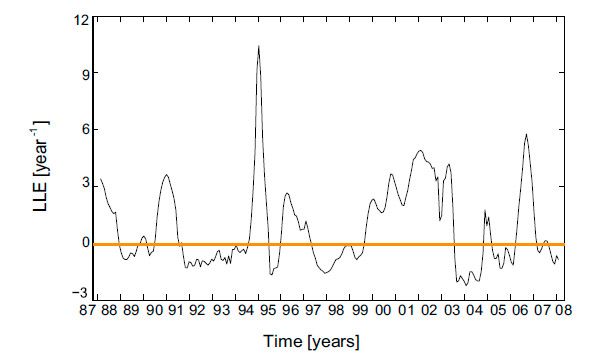
Рис. 3. Динамика трансформации локального ляпуновского показателя, вычисляемого по 180-дневным промежуткам. Хороший показатель говорит о нарастании малых различий в составе сообщества, отрицательный — об их уменьшении. Рисунок из обсуждаемой статьи в PNAS

Дабы лучше разобраться в динамике исследуемой сукцессии, ученые смоделировали совокупность с помощью несложной «модели занятия мест» (patch-occupancy model). Модель обрисовывает изменение доли неспециализированной площади, занятой каждым из трех видов, и исходит из предположения, что целый участок складывается из солидного числа отдельных мест, каждое из которых возможно занято лишь одной особью. Модель, по-видимому, чуть ли не несложная из вероятных: она не содержит никаких более сложных догадок о характере влияния одного вида на другой.

Единственное усложнение — это добавленное в модель влияние температуры на смертность корковых мидий и водорослей: чем теплее, тем больше у них смертность (как мы знаем, что в жару эти организмы гибнут от подсыхания). Сами колебания температуры описывались несложной синусоидой (на рис. 2, А видно, что температура вправду изменяется достаточно систематично, в отличие от численностей видов).

Кроме того такая несложная модель достаточно хорошо обрисовывала сообщество. В отсутствии догадок о влиянии температуры на смертность совокупность показывала затухающие колебания с периодом около 1,5 лет и в финише финишей приходила к стационарному состоянию (рис. 4, А–F): площади, занятые каждым видом, достигали стабильного значения и потом не изменялись. А вот введение регулярных (в полной мере предсказуемых!) колебаний температуры приводило к хаотическому поведению (рис. 4, G–L). Вейвлет-анализ показываемых моделью колебаний продемонстрировал, что, как и в действительности, выделяется период около двух лет; глобальный ляпуновский показатель был близок к реально замечаемому значению (+0,82 год–1), и в данном случае кроме того значимо отличался от нуля (наблюдения и модель — это различные комплекты данных, и во втором случае удалось существенно сузить диапазон вероятных значений). Наряду с этим локальные ляпуновские показатели, как и в действительности, кроме этого «скакали» между хорошими и отрицательными значениями.

Авторы вычисляют результаты моделирования указанием на то, что в изученной ими экосистеме вправду имеет место хаотическое поведение, а не «продолжительная дорога к равновесию», которую исследователи застали в самом начале.

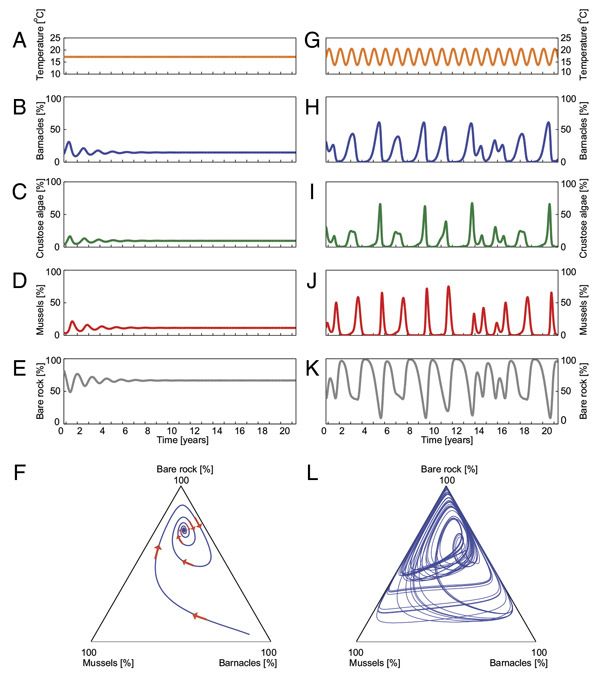
Рис. 4. Динамика трансформации состава сообщества в «модели занятия мест». Не учитывая колебаний температуры модель приходит к стационарному состоянию (A–F).

Продемонстрирована динамика трансформации с течением времени: температуры (А) и количества морских уточек (B), корковых водорослей (С), мидий (D), обнажённых камней (Е), а кроме этого фазовый портрет совокупности (F). Любая точка на фазовом портрете изображает состояние экосистемы, характеризующееся комплектом площадей камней, занятых мидиями, занятых морскими уточками и свободных от организмов (площадь, занятая корковыми водорослями, конкретно определяется из этих данных); траектория (отмечена синей линией с красными стрелками) показывает, как будет изменяться со временем состав экосистемы. При наличии сезонных колебаний модель демонстрирует хаотическое поведение (G–L, графики отражают те же параметры, что и в левой колонке). Рисунок из обсуждаемой статьи в PNAS

Но, население прибрежных камней не демонстрирует настоящий хаос: совокупность иногда переключается с хаотического режима на стабилизирующийся и обратно. Биологические совокупности, находящиеся, подобно данной, «на краю хаоса», были известны и ранее, но ни при каких обстоятельствах они не относились к многовидовым сообществам.

Необходимо подчеркнуть, что к хаотическому поведению экосистему подталкивает закономерное внешнее действие, а не случайный шум (введение в модель случайных ежедневных колебаний температуры в дополнение к сезонным не поменяло результаты принципиально) либо нерегулярно случающиеся катастрофические действия. К примеру, в некоторых вторых прибрежных сообществах цикличность сукцессий появляется по причине того, что штормы уносят мидиевые поселения (см.: R. T. Paine, S. A. Levin, 1981. Intertidal landscapes: Disturbance and the dynamics of pattern. ). Но в данном случае мидии образуют через чур узкий слой, дабы оказывать значительное сопротивление воде — кроме того по окончании сильнейших штормов они не обнаруживали никаких разрушений.

Подобные долгосрочные наблюдения (напомню, что в работе использованы эти за двадцать лет!) нужны для лучшего понимания того, как трудятся экосистемы. Так как математики от экологии достаточно давно предсказали существование хаотического поведения в многовидовых совокупностях — но лишь на данный момент оно было реально показано. А математическая модель немногого стоит, пока не показано, что она имеет отношение к действительности. Изучение хаотической динамики экосистем — это уже не только теоретическое знание, оно нужно для прогнозирования действия человека на природу, в том числе и чтобы повысить эффективность мероприятий по охране экологии.

Далеко не всегда в природе отмечается пресловутый «экологический баланс» — в случае, если, само собой разумеется, понимать его лишь как неизменность.

Источник: Elisa Benincà, Bill Ballantine, Stephen P. Ellner, and Jef Huisman. Species fluctuations sustained by a cyclic succession at the edge of chaos // Proceedings of the National Academy of Sciences. 2015.

V. 112. № 20. P. 6389–6394.

Сергей Лысенков