ПК обогнал суперкомпьютеры в ответе задачи трехчастичного рассеяния

Рис. 1. Сверху: суперкомпьютер JUGENE (Julich Blue Gene) занимает целый зал в Юлихском исследовательском центре (Forschungszentrum Julich) в Германии, фото с сайта thinkedition.net. Данный суперкомпьютер был создан в 2007 году компанией IBM на базе архитектуры Blue Gene. В 2013 году его заменили на усовершенствованный вариант JUQUEEN, применяв новую версию данной архитектуры.

Оба суперкомпьютера в начале работы были замечательнейшими в Европе. Снизу: видеокарта GeForce GTX 970 (длиной около 25 см), использованная для ответа задачи трехчастичного рассеяния в обсуждаемой работе, фото с сайта geforce.com

Непростые задачи, для ответа которых требуется громадная вычислительная мощность, систематично появляются в различных областях наук. Естественный ответ на это— производительности суперкомпьютеров и рост числа. Но вычислительное время на них так же, как и прежде остается дорогим, а борьба научных коллективов за него — высокой.

Российские физики из НИИЯФ МГУ имени М. В. Ломоносова нашли второй подход к одной из ответственных ресурсоемких задач квантовой теории рассеяния. Они смогли свести ответ уравнений Фаддеева к виду, в котором максимально употребляются сильные стороны видеоплаты простого ПК: многопоточное параллельное исполнение однообразных процедур. Результат открывает много возможностей для ответа многих вторых вычислительных задач.

сложные задачи и Суперкомпьютеры

В настоящее время отмечается стремительный рост потребностей в высокопроизводительных вычислениях во всех областях естественных наук. Это позвано как потребностями математического (компьютерного) моделирования сложных многостадийных процессов, характеризующихся наличием солидного числа степеней свободы (такие процессы видятся, к примеру, в гидро- и газодинамике, теории плазмы, астрофизике, ядерной физике, теории поля на решетках и т. д.), так и переходом к правильному численному ответу многомерных дифференциальных и интегральных уравнений в реалистичной постановке. Как в полной мере естественный ответ на эти новые запросы на данный момент отмечается стремительный рост установленной производительности и числа суперкомпьютеров по всему миру, причем самый быстрый рост пиковой производительности супермашин отмечается в Китае и США (см. рейтинг TOP500).

К примеру, самый «замечательный» суперкомпьютер по состоянию на июль 2016 года — китайский Sunway TaihuLight — имеет производительность порядка 100 петафлопс, что в три раза больше, чем у прошлого фаворита, и в много раза больше свойств суперкомпьютеров начала XXI века.

В квантовой теории рассеяния имеется также класс задач, предъявляющих большие требования к вычислительным ресурсам. Речь заходит о правильном ответе (в численном смысле) задач рассеяния с несколькими частицами (так именуемые few-body systems) в постоянном спектре. Напомним читателю, что связанные состояния совокупностей, в то время, когда перемещение частиц ограничено, владеют фиксированными (квантованными) энергиями и тем самым отвечают области дискретного спектра гамильтониана совокупности.

В настоящее время в полной мере допустимо бережно вычислить дискретные спектры совокупностей, складывающихся из многих сотен а также тысяч частиц (таких как ядра и электроны атомов), что, в частности, включает в себя точный расчет больших молекул и структуры атомов (этим занимается квантовая химия). Но рассеяние частиц соответствует их неограниченному перемещению, исходя из этого состояния рассеяния существуют для постоянного (континуального) комплекта энергий и так отвечают области постоянного спектра гамильтониана совокупности. Кроме этого при одной энергии вероятны разные варианты (каналы) рассеяния для одной и той же совокупности.

Так, задачи в постоянном спектре являются как следует вторыми и намного более сложными, чем задачи дискретного спектра. Неудивительно исходя из этого, что ответ квантовой задачи рассеяния уже трех частиц приводит к большим трудностям, причем как в чисто математическом, так и в вычислительном замысле.

Важность правильного ответа задачи трехчастичного рассеяния (и задач для большего числа частиц) в квантовой механике обусловлена тем, что оно весьма чувствительно к внутренней структуре разглядываемых квантовых совокупностей и разрешает как бы посмотреть вовнутрь атомов и ядер и отыскать ключи к последовательности ответственных неприятностей современной физики (к примеру, лучше осознать природу ядерных сил). К тому же многие физические задачи, такие как рассеяние дейтронов на ядрах и нуклонах, рассеяние последовательности легких ядер (6,7Li, 13C и т. д.) на вторых ядрах либо рассеяние позитронов и электронов на молекулах и атомах, и последовательность задач в физике жёсткого тела и т. д., смогут быть обрисованы в рамках квантовой модели трех частиц.

Отыщем в памяти кроме этого, что математически строгое ответ кроме того ньютоновской задачи трех тел в хорошей механике, в частности, изучение поведения совокупности Почва — Луна — Солнце в полном виде не отыскано до сих пор, не обращая внимания на фундаментальные изучения многих великих математиков в данной области, включая Лагранжа, Пуанкаре и других.

С математической точки зрения квантовая задача рассеяния трех тел думается никак не несложнее, а возможно, кроме того значительно сложнее хорошей. К примеру, до сих пор нет математически строгого ответа задачи трех кулоновских частиц (то имеется взаимодействующих приятель с втором по закону Кулона) при энергиях выше трехчастичного порога и т. д. Однако, громадный прогресс был достигнут в работах известного советского и российского математика Людвига Фаддеева, что выстроил строгую математическую теорию для квантовой задачи трех тел (Л. Д. Фаддеев, 1966. «Математические вопросы квантовой теории рассеяния для совокупности трех частиц»), отыскал математически верное уравнение для задачи трехчастичного рассеяния и сформулировал условие разрешимости этих уравнений, каковые сейчас везде в мире известны как уравнения Фаддеева.

Эта во всех смыслах пионерская работа Фаддеева со времени собственного появления в начале 60-х годов прошлого века, привела к огромному резонансу во многих разделах теоретической и ядерной физики и стимулировала громадной поток ежегодных конференций во всем мире по так называемым малочастичным совокупностям. (В настоящее время в мире систематично проводится по крайней мере три серии «малочастичных» конференций: мировая, европейская и Азиатско-Тихоокеанская, любая с частотой раз в три года. В текущем году европейская конференция проходит в середине августа в Дании. Напомним, что намедни на данной конференции было издано постановление об учреждении медали имени Людвига Фаддеева, которой будут отмечаться ученые, внесшие выдающийся вклад в квантовую теорию нескольких частиц.) Причем большая часть изучений, представленных на этих конференциях, в особенности в начальные годы по окончании выхода пионерских работ Фаддеева, была посвящена способам ответа его уравнений и разным аппроксимациям в задаче рассеяния трех тел.

Это было обусловлено тем, что в неспециализированном виде уравнения Фаддеева, к примеру, в интегральной формулировке являются громадную совокупность многомерных сингулярных интегральных уравнений, причем интегралы в ядре этих уравнений берутся с переменными пределами, зависящими от вторых переменных. Это, в частности, ведет к тому, что прямые итерации таких уравнений (в то время, когда в правую часть последовательно подставляется ответ, обнаруженное прошлом шаге итерации) выясняются неосуществимыми, так как малоизвестные функции в левой и правой частях уравнения выяснены для различных доводов. В итоге при итерациях приходится переинтерполировать текущее ответ в каждой точке на огромной многомерной решетке.

Это ведет к необходимости многомерных интерполяций текущего ответа на каждом шаге итераций, неспециализированное число таких переинтерполяций достигает миллионов а также десятков миллионов. Ко мне необходимо еще добавить неприятности с регуляризацией сложных сингулярностей в ядре уравнений Фаддеева и весьма громоздкие схемы нахождения матриц перевязки солидного числа угловых моментов квантовых частиц, что ведет к суммам по промежуточным проекциям угловых моментов частиц высокой кратности (впредь до 30-кратных сумм) для нахождения каждого матричного элемента матрицы ядра (а таких матричных элементов в настоящей задаче возможно довольно много миллионов а также миллиардов).

В итоге вычислительная сложность ответа уравнений Фаддеева для настоящих задач в ядерной и ядерной физике была таковой, что впредь до появления громадных суперкомпьютеров, в большинстве случаев в США, в ередине 80-х годов прошлого века, отыскать правильное ответ таковой задачи за приемлемое время было нереально. Более того, в финише 80-х годов время ответа полной трехчастичной фаддеевской задачи на громадном американском суперкомпьютере составляло 2–3 семь дней (см., к примеру, статью A. Picklesimer, R. A. Rice, and R. Brandenburg, 1991. ? degrees of freedom in trinuclei: I. The Hannover one-? model и другие статьи этого коллектива авторов из серии «? degrees of freedom in trinuclei»). Было очевидно, что никакой простой компьютер с таким количеством вычислений не справится. Но весьма стремительный прогресс в вычислительной технике, достигнутый в последние десять лет, превзошел самые храбрые ожидания и самые наглые грезы. И сейчас ответ полной совокупности фаддеевских уравнений для трехчастичной совокупности возможно взять на простой настольном компьютере за 15–30 мин..

Статья группы русских ученых с результатом размещена в июльском номере Computer Physics Communications.

дискретизация и Волновые пакеты постоянного спектра квантовой совокупности

В базе подхода, разрешающего решать задачи рассеяния практически так же легко, как задачи на связанные состояния совокупностей, лежит мысль дискретизации постоянного спектра. Наряду с этим переход от правильных волновых функций постоянного спектра, каковые не имеют конечной нормы, кмножеству дискретных нормируемых функций возможно сделан многими методами. Но, по-видимому, одним из самые удобных и естественных способов есть переход к так называемым стационарным волновым пакетам, введенным в первый раз в теории дифференциальных уравнений (называющиеся «личные дифференциалы») учениками Гильберта Эрнстом Хеллингером и Германом Вейлем еще в начале прошлого века, и использованные потом Вигнером на заре развития квантовой механики.

Сущность этого подхода в его современной интерпретации пребывает в разбиении постоянного спектра гамильтониана совокупности на полосы (бины) конечной ширины ?. В каждой таковой полосе из правильных функций постоянного спектра методом интегрирования по энергии строится волновой пакет (потому, что он не зависит от времени, мы именуем его стационарным). В результате, получается дискретный комплект пакетированных состояний постоянного спектра, что в предстоящем употребляется как базис для вычислений.

направляться подчернуть, что интегрирования по полосам дискретизации оказывается достаточно, дабы волновые функции стали нормируемыми подобно функциям дискретного спектра. Отличие таких пакетных состояний от связанных состояний гамильтониана пребывает в том, что мы можем строить разбиения постоянного спектра произвольным образом, наряду с этим энергии пакетных состояний будут задаваться разными сетками дискретизации. В пределе бесконечно малых ширин разбиения, результаты полученные в таких разных базисах стремятся к правильному ответу для исходного постоянного спектра

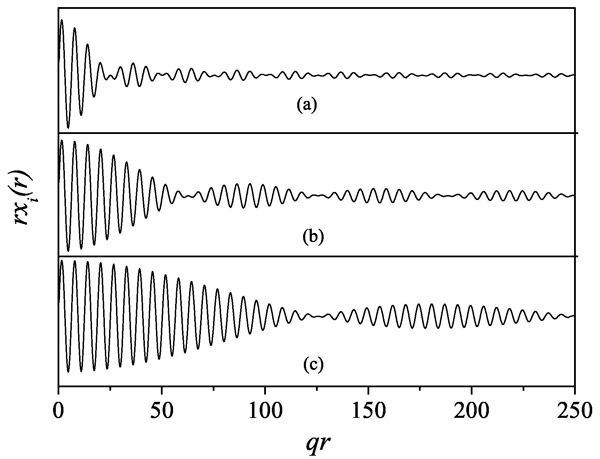
Рис. 2. Поведение нескольких волновых пакетов в зависимости от безразмерной координаты qr, где q — импульс частицы, для бинов различной ширины. (а) — график для достаточно широких промежутков разбиения, (b) — для средних, (с) — для промежутков с маленькой шириной. Как видно из рисунка, при малых ширинах волновые функции распространяются на большие расстояния

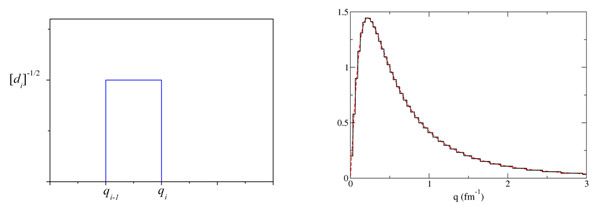
В импульсном пространстве волновой пакет имеет форму одиночного импульса (рис. 3, слева), а пакетированная волновая функция (к примеру, волновая функция дейтрона — протона и связанного состояния нейтрона) имеет форму гистограммы (рис. 2, справа).

Рис. 3. Представление в импульсном пространстве волнового пакета (слева) и пакетированной волновой функции (справа). Видно, что волновая функция представляется в виде ступенчатого графика (гистограммы)

Так, мы приобретаем весьма эргономичный метод дискретного представления всех волновых функций, и операторов в импульсном пространстве в виде одно-, двух-, трехмерной (либо многомерной) гистограммы. С таковой гистограммой легко проводить каждые вычисления матричных элементов операторов в квантовой теории, так как интеграл по каждой ступени возможно заменить (по теореме о среднем) произведением значения подынтегральной функции на данной ступени на ширину бина (либо на площадь прямоугольной площадки, на количество параллелепипеда и без того потом для многомерных объектов).

К примеру, вместо интегрального уравнения Липпмана-Швингера для t-матрицы, обрисовывающей рассеяние частицы силовым полем V в квантовой механике возьмём простое матричное уравнение

где все операторы представлены матрицами в пакетном базисе и gk –элемент матрицы свободной резольвенты, имеющей диагональный вид. Причем, благодаря дополнительному сглаживанию энергетических зависимостей операторов по полосам дискретизации, которое мы используем, особенности исходного интегрального ядра сглаживаются, и вместо сингулярного интегрального уравнения приобретаем легко решаемое матричное уравнение.

Такую же редукцию на дискретное пакетное пространство возможно сделать и для квантовых задач рассеяния трех, четырех и большего числа частиц. Главное отличие от рассмотренной тут несложной задачи рассеяния будет в размерности интегрального ядра и в характере исходной сингулярности по энергии. Но в любом случае эти сингулярности при пакетировании сглаживаются, и в итоге все равно получается многомерное матричное уравнение с матрицами, элементы которых уже не содержат изюминок по импульсам и энергиям.

Наряду с этим вся трудоемкость задачи перекладывается на размерность применяемых пакетных базисов и заполнение элементов матриц соответствующих операторов, а не на многомерные переинтерполяции текущих ответов с учетом сингулярностей ядер уравнений как в классическом подходе.

Значительным преимуществом пакетной схемы есть «пиксельная форма» матричных уравнений, в то время, когда элементы всех матриц вычисляются независимо друг от друга. Это разрешает довольно «несложно» распараллелить весьма трудоемкий расчет огромного числа матричных элементов многомерного интегрального ядра, так что время расчета при таковой массивно-параллельной реализации возможно очень сильно (то имеется в сотни и десятки раз) сократить. Для реализации этого успешным ответом есть применение графического процессора (GPU), либо видеоплаты, которой оснащен фактически любой компьютер для работы с компьютерной графикой. Очевидно, для таких массивно-параллельных вычислений подходит далеко не любая графическая карта, а лишь специальная под научные вычисления. Но они сейчас уже обширно представлены на рынке.

К примеру, компания NVIDIA в последние годы расширила собственную главную специализацию с разработки графических карт для игровых приставок на их адаптацию под чисто научные задачи. По большому счету, возможно заявить, что в связи с широким распространением графических вычислений во всех областях современной науки на отечественных глазах происходит компьютерная революция в научных вычислениях и широкий переход к массивно-параллельной реализации многих компьютерных программ.

«GPU — компьютерная революция»: что это такое?

Графическая карта — один из главных элементов игровых большинства и приставок компьютеров — разрешает в режиме настоящего времени генерировать скоро сменяющие друг друга картины на экране. Для данной цели графическая карта включает программируемые арифметические устройства — пиксельные шейдеры (pixel shaders), каковые разрешают вычислить состояние пикселя с координатами (x, y) на экране. В неспециализированном случае пиксельный шейдер приобретает на входе координату и другую дополнительную данные и обязан выдать конечный цвет данного пикселя, включая его освещенность, степень затенения и т. д.

Наряду с этим, потому, что при работе в масштабе настоящего времени изображение на мониторе (которое на данный момент уже включает миллионы пикселей) должно сменяться неоднократно за секунду, скорость этих графических устройств должна быть огромной.

В начале 2000-х годов для программистов, применяющих 3D-графику, были созданы специальные программные средства, OpenGL и DirectX, разрешающие писать инструкции для GPU. Но практически сходу им пришло в голову, что вместо цвета пикселя шейдер может вычислять любую величину, привязанную к координатам. В случае, если на вход подавать числовые эти, которые содержат не цвета, то ничего не мешает написать шейдер, делающий с ними произвольные вычисления.

Итог можно считать в программу, а GPU безразлично, как именно он интерпретируется. В итоге оказалось, что возможно применять весьма высокую скорость арифметических вычислений с помощью графической карты для многих целей, не имеющих ничего общего с графикой на компьютере. Для облегчения программирования кроме того была создана особая архитектура CUDA.

В следствии была создана настоящая возможность для сверхбыстрых вычислений с помощью массивно-параллельной реализации.

На данный момент серийные графические карты, каковые вольно продаются на рынке, включают в себя порядка 4 тысяч вычислительных ядер (а кое-какие — кроме того больше!). Сравните это с 4–8 ядрами для простого процессора. Они разрешают создавать параллельные вычисления при помощи многих сотен и десятков тысяч потоков — так называемых нитей (threads).

И не смотря на то, что скорость вычисления на протяжении каждой таковой нити пара уступает скорости центрального процессора, параллельное применение огромного числа нитей разрешает добиться ускорения на порядки размеров.

Но не все так легко. В силу главных изюминок собственной конструкции, GPU-вычисления выполняются в моде SIMD (single instruction on multiple data), что подразумевает, что вычисления на протяжении всех нитей должны быть выполнены по одной и той же инструкции (команде), и, следовательно, тут не допускаются переходы и условные операторы. Имеется и другие ограничения.

Исходя из этого сама возможность сверхбыстрых вычислений на GPU предполагает нетривиальное умение действенно распараллелить полную задачу с учетом ограничений, налагаемых SIMD-модой. Самый несложный и очевидный пример для громадного ускорения вычислений при помощи GPU — это вычисление элементов матрицы высокой размерности. В большинстве случаев для элементов таких матриц имеются аналитические формулы (различной степени сложности), и тогда полная матрица делится на довольно много тысяч либо миллионов блоков, причем матричные элементы в каждого блока считаются при помощи параллельных нитей (по одним и тем же формулам).

Но довольно часто полная матрица выясняется таковой высокой размерности, что она не помещается ни в кэш-память GPU, ни в стремительную память (RAM) компьютера, и ее возможно записать лишь на жесткий диск. Но наряду с этим многократное считывание кусков матрицы с диска занимает так много времени, что целый выигрыш от параллельной реализации исчезает. Однако, имеется довольно много способов обойти эти ограничения и добиться высокой степени ускорения GPU-вычислений.

На сегодня ультрабыстрые GPU-вычисления внедрены в много научных приложений и проектов, в частности, в квантовой физике многих тел, в квантовой теории поля, химии громадных молекул, в геофизике, медицине, денежной математике и т.д. Наряду с этим во многих приложениях применение GPU-вычислений дает совсем неповторимые новые возможности (см., к примеру, книги «Разработка CUDA в примерах. Введение в программирование графических процессоров» и «CUDA Fortran для инженеров и учёных»).

Применение GPU-вычислений в квантовой теории многочастичного рассеяния

При ответе квантовых задач многочастичного рассеяния на GPU приходится иметь дело с уравнениями для амплитуды трехчастичного рассеяния Фаддеева в форме, предложенной германскими теоретиками Альтом, Гроссбергером и Сандхасом. В пакетном представлении матричный аналог этого уравнения для совокупности трех нуклонов (к примеру, для описания рассеяния нейтрона на дейтроне) имеет форму:

где U — искомая матрица оператора перехода, V — матрица оператора сотрудничества двух частиц (которая имеет несложную блочную структуру) и G1 — матрица резольвенты гамильтониана канала (имеющая диагональный вид). Самым сложным с технической точки зрения элементом этого уравнения есть матрица оператора перестановки P, которая имеет полную размерность совокупности

Дабы понизить размерность этого уравнения, в большинстве случаев выполняется разложение всех операторов по сферическим гармоникам, после этого оказавшиеся угловые моменты по каждой (из двух) координат Якоби связываются с переменными изоспина и спина. В итоге для полного момента всей совокупности J получается огромная совокупность зацепляющихся многомерных интегральных уравнений (в среднем 40–60 зацепляющихся уравнений для каждого значения J). Для решения всего одного из этих уравнений необходимо сделать дискретизацию, отвечающую проектированию на базис стационарных волновых пакетов с применением 50–100 бинов по каждой координате Якоби.

Тогда в среднем получается совокупность алгебраических уравнений порядка N = 104?60 = 600 000, с полной размерностью матрицы N?N. Такая матрица складывается из 300–500 миллиардов матричных элементов, так что она не влезает в стремительной памяти компьютера, ее возможно разместить лишь на громадном твёрдом диске. К счастью, главная матрица оператора перестановки представляется в виде , где O — блочная матрица и P0 — весьма разреженная матрица перекрывания для плосковолновых функций в разных комплектах трехчастичных импульсов, которая заполнена чуть ли на 1% (либо кроме того меньше). Это разрешает разместить матрицу P0 в оперативной памяти, но появляется необходимость предварительной проверки всех ее отбора и элементов среди них хороших от нуля.

Такая проверка миллиардов матричных элементов также требует довольно много компьютерного времени. И, наконец, направляться упомянуть, что вся эта огромная работа обязана выполняться для каждого значения полного момента J, которое может принимать полуцелые значения 1/2, 3/2, …, 17/2!

Оказалось, что распараллеливание на десятки тысяч потоков разрешает выполнить всю эту огромную численную работу на простом персональном компьютере за приемлемое время.

Неспециализированная схема ответа задачи в пакетном представлении складывается из следующих шагов:
    1) заполнение сеток дискретизации для каждого комплекта импульсных координат, и вычисление блочных матриц V, O и диагональной матрицы G1;
    2) предварительный отбор ненулевых элементов матрицы P0;
    3) вычисление ненулевых элементов матрицы P0;
    4) ответ матричного уравнения способом итераций.

Потому, что самыми трудоемкими в данной схеме являются шаги 2) и 3), мы совершили распараллеливание конкретно для них. Наряду с этим скорость вычислений возрастает на порядки размеров и достигает фантастических значений для распараллеленных частей полной программы в случае довольно несложного вида двухчастичных сотрудничеств. В частности, мы нашли, что полная матрица перекрывания P0 содержит приблизительно (для фиксированного J) 260 миллионов ненулевых элементов, при заполнении каждого из которых требуется численно посчитать двойной интеграл от полиномов Лежандра большого порядка в комбинации с серией вторых арифметических операций.

Мы с громадным удивлением поняли, что при массивно-параллельном вычислении этих 260 миллионов сложных интегралов на простом ПК с графическим процессором GeForce GTX 670 для этого требуется всего 3 секунды, а с учетом их предварительного отбора — всего 8 секунд.

направляться тут подчернуть, что процедура предварительного отбора ненулевых элементов матрицы разрешает не только уменьшить количество применяемой памяти, но и значительно серьёзна для ускорения процедуры распараллеливания на GPU. Дело в том, что прямое вычисление элементов разреженной матрицы на GPU неэффективно, потому, что параллельные потоки оказываются загружены неравномерно, и большинство процессоров вынуждена простаивать, пока остальные делают вычисления. По окончании же предварительно отбора ненулевых элементов (что нам кроме этого удалось распараллелить!), параллельных потоков необходимо намного меньше и они загружены равномерно.

Данный пример светло показывает, каких поразительно высоких скоростей возможно достигнуть при отлично организованном вычислительном ходе на GPU.

В итоге полное ответ огромной совокупности зацепляющихся интегральных уравнений для всех нужных J (с учетом всех шагов, среди них и делаемых последовательно) для абсолютно реалистических сложных двухчастичных сотрудничеств возможно выполнить за время порядка 15–30 мин.. По контрасту, та же Фаддеевская задача на солидном суперкомпьютере Blue Gene может занимать более одного дня и дорого стоит.

Нет никаких сомнений в том, что очень много вторых ответственных вычислительных задач, требующих при простой (то имеется последовательной) реализации огромных вычислительных ресурсов, возможно решить на базе современных графических процессоров на простом компьютере за довольно маленькое время. Это обещает открыть воистину фантастические новые возможности в симуляции и математическом моделировании настоящих процессов на компьютере в большинстве областей современной науки. Так что мы находимся практически в самом начале этого занимательного пути.

Источник: V. N. Pomerantsev, V. I. Kukulin, O. A. Rubtsova, S. K. Sakhiev. Fast GPU-based calculations in few-body quantum scattering // Computer Physics Communications. 2016. V. 204.

P. 121–131.

Владимир Кукулин