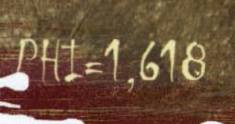
Формула золотого сечения

Приводим универсальную формулу Золотого Сечения или кода золотой пропорции, предложенного А. П. Стаховым в статье 8-го выпуска журнала «Украинский математический журнал» за 2004 год. В статье описан подход к геометрическому определению числа Фибоначчи и содержит ряд выводов фундаментального характера.

Обобщение задачи о Золотом Сечении

Прежде всего, профессор Стахов А.П. обобщил задачу о Золотом Се­чении. Суть этого обобщения предельно проста. Если задаться не­отрицательным целым числом р = 0, 1, 2, 3, … и разделить отрезок “AB” точкой С в такой пропорции, чтобы было:

CB/AC=(AB/CB)

x^p+1 = x^p + 1,

корни которого называются обобщенными Золотыми Пропорциями или Золотыми р-пропорциями t_p. Давайте вдумаемся в этот результат. В течение нескольких тысячелетий, начиная с Пифагора и Платона, человечество пользовалось широко известным классическим Золотым Сечением, которое считалось единственным, уникальным и неповторимым. И вот в конце 20-го века украинский ученый Стахов обобщает эту задачу  и доказывает существование бесконечного числа Золотых Сечений! И все они имеют такое же право на существование, как и классическое Золотое Сечение. Более того, Стахов показывает, что Золотые р-пропорции t_p (1£t_p£2) представляют собой новый класс иррациональных чисел, которые выражают некоторые неизвестные нам до этого математические свойства  треугольника Паскаля. Ясно, что такой математический результат имеет фундаментальное значение для развития современной науки и математики.

Коды Золотой р-пропорции. Используя понятие Золотой р-пропорции, Стахов затем  вводит новое определение действительного числа в виде:

(a_iÎ{0,1}), которое он назвал «Кодом Золотой р-пропорции». Стахов показывает, что это понятие, которое он назвал «Кодом Золотой р-пропорции». Стахов показывает, что это представление, которое является становлением знаменитого «Ньютоновского определения» действительного числа, может быть положено в основу новой теории действительных чисел. Дальше он показывает, что данный итог имеет значимое прикладное значение и может привести к созданию твердо новой компьютерной арифметики и новых компьютеров, компьютеров Фибоначчи. И Стахов не только провозглашает идею «компьютеров Фибоначчи», но и возглавляет и организует инженерные планы по созданию таких компьютеров в Винницком политехническом университете (1977-1995). 65 зарубежных патентов на изобретения в области «компьютеров Фибоначчи», выданных государственными патентными ведомствами США, Японии, Великобритании, Франции, Германии, Канады и др. стран, подтверждают приоритет украинской науки (и приоритет проф. Стахова) в этой значимой компьютерной области.

Математика гармонии

В последние десятилетия область научных интересов академика Стахова все больше сдвигается в область оснований математики и компьютерной науки. Об этом, скажем, свидетельствует его лекция «Золотое Сечение и современная Математика Гармонии», прочитанная им на заседании 7-й Интернациональной конференции «Числа Фибоначчи и их приложения» (Австрия, Грац, 1996) и после этого повторенная в 1998 г. на заседании Украинского математического общества. Эта лекция произвела огромное впечатление на украинских математиков и вызвала оживленную дискуссию.

В настоящее время А.П. Стахов является энергично работающим ученым, публикующим статьи в знаменитых интернациональных журналах. Вследствие отличному познанию английского языка ему за короткий срок (1 год) удалось опубликовать 8 фундаментальных статей в Интернациональном междисциплинарном журнале “Chaos, Solitons and Fractals” (England). Это – бесспорно большой триумф не только проф. Стахова, но и каждой украинской науки. Вследствие проф. Стахову о научных достижениях украинской науки узнала научная общественность Запада.

Этими статьями проф. Стахов по существу закончил цикл многолетних изысканий по созданию нового направления в математике – Математики Гармоники. Возникает вопрос, какое место в всеобщей теории математики занимает сделанная Стаховым Математика Гармонии? Мне представляется, что в последние века, как выразился когда-то Н.И. Лобачевский, «математики все свое внимание обратили на высшие части Аналитики, пренебрегая началами и не желая работать над обрабатыванием такого поля, которое они теснее раз перешли и оставили за собою». В итоге между «элементарной математикой», лежащей в основе современного математического образования, и «высшей математикой» образовался обрыв. И данный обрыв, как мне кажется, и заполняет Математика Гармоники, разработанная А.П. Стаховым. То есть «Математика Гармонии» – это огромный теоретический взнос в становление раньше каждого «элементарной математики», и отсель вытекает значимое значение «Математики Гармонии» для математического образования.

Следует подметить также огромную организационную работу проф. Стахова по стимулированию изысканий в области чисел Фибоначчи и Золотого Сечения и распространению познаний о Золотом Сечении среди широких кругов научной общественности. В 2003 г. по инициативе и под начальством проф. Стахова в Виннице была проведена Интернациональная конференция «Проблемы Гармоники, Симметрии и Золотого Сечения в Природе, Науке и Искусстве». На этой конференции проф. Стахов был избран Президентом Интернационального Клуба Золотого Сечения, то есть в реальное время проф. Стахов имеет формальный ранг главы нового научного направления по теории Золотого Сечения, энергично развиваемого в нынешней науке. И это избрание является, безоговорочно, интернациональным признанием выдающихся заслуг проф. Стахова в области теории чисел Фибоначчи и Золотого Сечения.

Я с интересом познакомился с программой математического курса «Математика Гармоники и Золотого Сечения», предлагаемой проф. Стаховым для физико-математических факультетов педагогических институтов. По существу эта программа – ни что иное, как начало преобразования математического образования, основанного на тезисах Гармоники и Золотого Сечения. И если учесть, что такой курс теснее прочитан проф. Стаховым в течение 2001-2002 года для студентов физико-математического факультета Винницкого государственного педагогического института, то дозволено считать, что такая преобразование теснее началась в Украине (в Винницком педагогическом институте). У меня нет никаких сомнений в полезности этого курса для грядущих учителей математики и физики. Я думаю, что проф. Стахов имеет большой ученый потенциал, Дабы написать учебник по этому курсу для педагогических институтов, а также учебник «Математика Золотого Сечения»для средних школ и тем самым закончить предложенную им реформу современного математического образования.

Я не сомневаюсь, что сделанное проф. Стаховым новое научное направление, названное им «Математикой Гармонии», имеет большое междисциплинарное значение, так как затрагивает основания многих наук, включая математику, теоретическую физику, компьютерные науки, а предложенный им план преобразования математического образования на основе идей Гармоники и Золотого Сечения, открывает новые пути в становлении математического и всеобщего образования. И это будет содействовать выработке у учащихся нового научного мировидения, основанного на тезисах Гармоники и Золотого Сечения.