Содержание
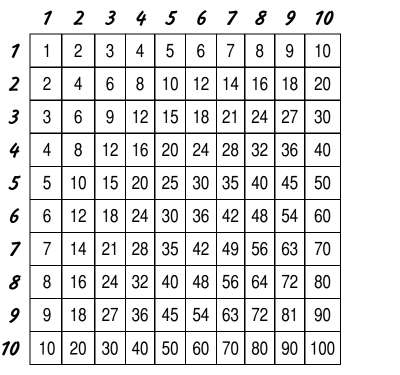
Квадрат таблицы умножения
Для того чтобы выучить таблицу умножения, предлагаем рассмотреть квадрат составленный из результатов таблицы умножения и закономерностей этого квадрата.
Закономерности квадрата таблицы умножения
Все мы в школе изучали таблицу умножения. Но не все знают закономерности таблицы если её выстроить в виде квадрата. Зная свойства квадрата таблицы умножения её довольно легко освоить и запомнить. Предлагаем Вам данный лайфхак для запоминания таблицы умножения легко и беззаботно.
Итак квадрат из таблицы умножения составляется таким образом, чтобы все результаты умножения от 1х1 до 10х10 были расположены . Всего здесь 100 результатов. В первую очередь давайте избавимся от некоторых из них.
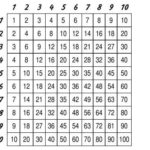
При умножении на 10 в конец числа просто добавляется ноль. Это через чур легко и при переходе к умножению действительно сложных чисел нам не пригодится. Так что исключим из таблицы 10-ю строчку и 10-й столбик.
Треугольник из таблицы умножения
Теперь уберём из таблицы повторяющиеся результаты умножения. Если поменять местами множители местами, ответ останется тем же. К примеру, и 3х7 и 7х3 равняется 21. Исходя из этого уберем из таблицы повторы.
Итак, мы избавились от половины ячеек и получили треугольник с нижеперечисленными свойствами.
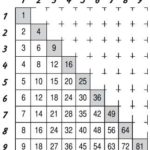
Числа в серых ячейках являются ни чем иным, как квадратами целых чисел, или просто квадратами. Это результаты перемножения каждого числа самого на себя. К примеру, вдоль каждой стороны шахматной доски 8 клеток, исходя из этого полное количество клеток на доске будет равняться восьми в квадрате. Записывают это так: 82, что соответствует 8х8 = 64.
Если нет желания заучивать таблицу умножения, имеется возможность заполнить ее ячейки еще одним методом. Сначала можно просто складывать нечетные числа 1, 3, 5, 7 и т. д. Начинаем с 1 + 3 = 4. После этого прибавлять 5, получим 9, после этого 7, получим 16… Так нам удастся вычислить квадраты всех чисел.
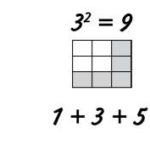Если взять любую ячейку с квадратом числа и вычитать из нее нечетные числа, начиная с 1, то получатся значения по диагонали, идущей в другую сторону от исходной ячейки.
Так, начав с 36 и отняв 1, получим 35, отняв 3, получим 32, вычтя 5, получим 27.
(Сравнив эту диаграмму с таблицей умножения, вы убедитесь, что все сходится.)
Аналогичным методом, но посредством четных чисел (2, 4, 6, 8…) возможно заполнить и остальные ячейки. Взглянуть на диагональ, идущую ниже диагонали квадратов, ту, где стоят числа 2, 6, 12, 20… Эти значения возможно получить, начав с 2, после этого прибавив 4, после этого 6, позже 8 и т. д. А взяв любое из этих чисел (к примеру, 20), возможно определить значения вдоль идущей в другую сторону диагонали — вычитая 2, после этого 4, позже 6 (к примеру, 20 – 2 = 18, 18 – 4 = 14 и 14 – 6 = 8).
Такие последовательности нечетных и четных чисел позволяют вывести всю таблицу умножения, ни разу не сделав умножения как такового!
