Ученые просчитали покер

Рис. 1. Игра хедз-ап (heads-up) в покер. За столом двое игроков и крупье, сдающий им карты. Фото с сайта pokernews.com

В начале 2015 года в издании Science вышла статья, в которой было заявлено об успешном завершении работы компьютерной программы, просчитывавшей одну из предположений покера — хедз-ап в лимитном техасском холдеме. Программа обучилась принимать верное ответ в каждом из приблизительно 3,19×1014 вероятных состояний игры. Отысканная так стратегия на долгой расстоянии обязана обыгрывать остальные стратегии. Одним из результатов анализа стало подтверждение того, что дилер имеет преимущество перед вторым игроком.

Авторы статьи предлагают ведущим опытным игрокам в покер опробовать стратегию на практике и убедиться в ее оптимальности.

Техасский холдем (texas hold'em) — самая популярная разновидность покера. Игра ведется стандартной колодой из 52 карт. В начале каждого розыгрыша игроки приобретают по 2 карты (карманные карты).

Они наблюдают на собственные карты, по окончании чего происходит первый раунд торговли. Игрока, что начинает торговлю, именуют дилером (либо игроком на кнопке, см. Button (poker)), по окончании каждого розыгрыша дилером делается следущий по кругу игрок. На протяжении торговли игрок может поднять ставку (raise), уравнять ставку соперника (call) либо отказаться от предстоящего участия в розыгрыше и скинуть карты (fold).

В итоге по окончании раунда торговли любой оставшийся в розыгрыше игрок поставил на кон одну и ту же сумму денег. Потом для всех раскрываются три неспециализированные карты (flop), по окончании чего происходит второй раунд торговли. Затем раскрывается еще одна карта (turn), происходит третий раунд торговли.

Наконец, раскрывается пятая неспециализированная карта (river), и происходит последний, четвертый раунд торговли. В случае, если в какой-то момент в игре остается лишь один игрок, он забирает целый банк. В случае, если по окончании четвертого раунда торговли в игре остается более одного игрока, то они вскрывают собственные карманные карты и сравнивают оказавшиеся 5-карточные комбинации, каковые любой может выстроить из личных и неспециализированных карт.

Тот, у кого комбинация лучше, забирает банк.

Комбинации в покере

Комбинация составляется из двух карманных карт, каковые раздаются игрокам в начале игры, и пяти неспециализированных карт, каковые выкладываются на стол в ходе игры. В комбинации участвуют пять карт из этих семи. Комбинации перечислены по убыванию старшинства.

Роял-флеш (royal flush) — частный случай стрит-флэша, старший из всех вероятных, складывается из 5 старших (туз, король, женщина, валет, десять) карт одной масти.

Стрит-флеш (straight flush) — каждые пять карт одной масти по порядку.

Каре (four of a kind) — четыре карты одного преимущества.

Фул-хаус (full house) — пара и тройка.

Флеш (flush) — пять карт одной масти.

Стрит (straight) — пять карт по порядку любых мастей.

Сет (three of a kind, set) — три карты однообразного преимущества.

Две пары (two pairs) — две пары карт.

Пара (pair) — две карты одного преимущества.

Старшая карта (high card) — у игрока нет ни одной из вышеперечисленных комбинаций.

Хедз-ап (heads up) свидетельствует, что играются лишь два игрока. Лимитный покер — это версия игры, в которой ставки возможно повышать на фиксированную величину, причем повышать ставку возможно не более чем заблаговременно оговоренное число раз. Исходя из этого лимитный техасский холдем — это конечная игра.

Последовательные игры в теории игр принято задавать с помощью деревьев. Вершинам дерева будут соответствовать разные состояния игры. Каждой вершине приписано имя игрока, которому в данной вершине в собственности движение. Ребрам, исходящим из данной вершины, соответствуют действия, каковые может совершить данный игрок.

Одним из участников игры есть «природа» — так в теории игр именуют неестественного игрока, делающего роль генератора случайных чисел. «Природа» случайным образом решает, какую карту сдать игрокам либо открыть на столе.

Последовательные игры возможно поделить на два вида: игры с идеальной информацией (см. Perfect information) и игры с несовершенной информацией. В играх с идеальной информацией любой игрок постоянно знает, в какой вершине дерева он находится и что происходило до этого. В играх с несовершенной информацией игрок возможно не не сомневается в том, в каком состоянии находится игра.

Покер — пример игры с несовершенной информацией: игрок, не знает, какие конкретно карты находятся на руках у его соперника. Любой может замечать неспециализированные карты и совершаемые действия в момент торговли, но карты соперника в момент торговли известны не будут.

Любую конечную последовательную игру с идеальной информацией возможно просчитать с финиша, применяя метод обратной индукции. Разглядев одну подыгру самого последнего уровня (другими словами такую подыгру, на которой по окончании принятия любого решения игра заканчивается и игроки подсчитывают полученные платежи), возможно отыскать оптимальное воздействие игрока, у которого в собствености движение на данной подыгре. Потом совершенно верно так же возможно отыскать оптимальные действия игроков на всех подыграх последнего уровня. Затем, зная, как будут вести себя рациональные игроки на подыграх последнего уровня, возможно перейти к анализу игр предпоследнего уровня, и без того потом.

Непременно, совершенно верно окажется добраться до подыгры, совпадающей со всей игрой, по окончании чего возможно отыскать в ней оптимальное воздействие игрока, у которого в собствености первый движение. Так, будет отыскано оптимальное поведение всех игроков в любой вероятной ситуации и будет узнано, чем заканчивается игра при верных действиях всех игроков. Конкретно так в 2007 году были просчитаны шашки — оказалось, что при верной игре обеих сторон в шашках партия непременно закончится вничью (J. Schaeffer et al., 2007.

Checkers is solved).

Покер меньше шашек по количеству вероятных состояний игры. Но покер, в отличие от шашек, есть игрой с несовершенной информацией. Это делает неосуществимым прямое использование метода обратной индукции: в случае, если игрок в какой-то момент не знает, в какой из вершин он находится, то он не сможет отыскать конкретно оптимальное ответ. Однако такую игру возможно переписать в виде матрицы (обычная форма игры): по горизонтали возможно выписать все стратегии первого игрока, по вертикали — все стратегии второго игрока, по окончании чего в взятой матрице возможно отыскать равновесие Нэша. Теоретически.

Тут нас поджидает еще одна неприятность: полученная матрица для покера будет большой. Сложность нахождения равновесия Нэша с помощью метода линейного программирования растет экспоненциально при росте количества состояний игры, исходя из этого для сложных игр наподобие покера способ неприменим. Приходится оставить идею прямого сведения дерева к матрице.

Вместо этого авторы применяют особую модификацию критерия Сэвиджа (см. Regret (decision theory)), предназначенную для ответа игр с несовершенной информацией за линейное время от числа состояний игры. Метод просматривает с конца информационные множества и приписывает им тот либо другой штраф в зависимости от сыгранной стратегии. Затем метод минимизирует собранный штраф.

Еще одна трудность в ответе покера пребывала в том, что в нем ожидаемые платежи игроков выражаются не обязательно целыми числами — сравните с шашками, в которых вероятны всего 3 финала! Потому, что речь заходит о вычислении платежей компьютером, то авторам было нужно приближать нескончаемые десятичные дроби с заданным уровнем точности ε. Но тогда нельзя использовать стандартное определение равновесия Нэша, поскольку погрешность вычисления может помешать ответить на вопрос, выгодно ли кому-либо из игроков отклоняться от того либо иного профиля игры.

Авторы применяют концепцию ε-равновесия Нэша, в соответствии с которой профиль стратегий именуется ε-равновесием Нэша, в случае, если ни один из игроков, отклоняясь от этого профиля стратегий, не имеет возможности расширить собственную полезность более чем на ε. В частности, любое равновесие Нэша есть ε-равновесием Нэша.

Наконец мы подошли к результату, что взяли авторы статьи в Science. Для некоего малого ε авторы предъявили ε-равновесие Нэша (ε так мало, что людской жизни не хватит на диагностику отличия ε-равновесия Нэша от равновесия Нэша). На рис. 2 приведены действия игроков на первом ходу в этом профиле стратегий. Слева для любой стартовой комбинации двух карт указаны первые действия дилера (зеленая клетка — «повышать», красная — «сброс»), справа приведен ответ второго игрока, в случае, если дилер на первом ходу поднял ставку (зеленый цвет — «повышать», светло синий — «уравнивать», красный — «сброс», смешанные цвета соответствуют возможности смешивать с разными возможностями пара собственных стратегий).

В этом профиле дилер часто блефует — повышает ставку с нехорошей картой, а второй игрок достаточно довольно часто должен сбрасывать собственную карту, не будучи в силах выявить, блефует ли дилер. За счет этого дилер на долгой расстоянии обыгрывает второго игрока.

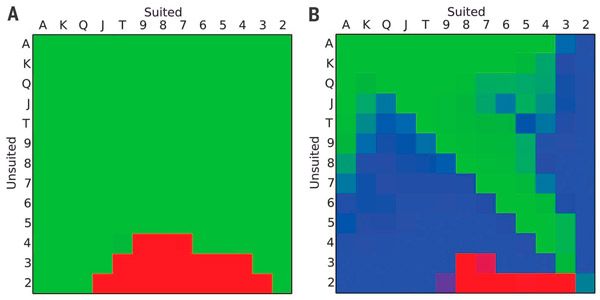
Рис. 2. Оптимальные действия игроков на первом ходу. Любая клетка таблицы соответствует одному из 169 вариантов карманной пары: в каждой масти 13 карт, наряду с этим в покере конкретная масть не серьёзна, а принципиально важно только, одной ли масти карманные карты (это увеличивает шансы на составление флеша); одномастным парам соответствуют клетки над основной диагональю (идущей из левого верхнего угла в правый нижний) таблицы (Suited), разномастным — клетки под данной диагональю. Цветами обозначены действия игроков: красный — скинуть карты, светло синий — уравнять ставку, зеленый — повысить ставку; смешанные цвета соответствуют сложным вариантам, при которых игрок может с некоторыми возможностями принимать различные ответы.

Слева — первый движение первого игрока, справа — ответный движение его оппонента в том случае, если первый игрок повысил ставку. Рисунок из обсуждаемой статьи в Science

В разглядываемой нами игре смогут существовать и другие ε-равновесия Нэша. Но направляться иметь в виду, что в игре с нулевой суммой, которой и есть покер, все равновесия Нэша приносят игрокам однообразные платежи. Исходя из этого нахождение одного равновесия Нэша свидетельствует, что отысканы стратегии, применяя каковые игроки смогут обеспечивать для себя наилучший вероятный итог.

Возможно ли получить, играясь отысканную стратегию? Да, в случае, если мочь воспроизводить действия, каковые предписывает выполнять стратегия в каждой позиции. Вряд ли на это будет способен человек — не хватит памяти. А вот против компьютера играться в лимитный хедз-ап сейчас безтолку. Вероятнее, это указывает, что не так долго осталось ждать лимитный хедз-ап покер пропадет с покерных сайтов — будет весьма сложно контролировать, что человек не применяет особые программы, помогающие отыскать оптимальные ответы.

Но игрокам в покер расстраиваться рано. Кроме того в случае, если про все вариации лимитного покера в один раз всё станет известно, останется анлимитный покер (возможно делать ставки любого размера), что не есть конечной игрой. Вследствие этого решить анлимитный покер модификациями метода обратной индукции уже вряд ли окажется…

Источник: M. Bowling, N. Burch, M. Johanson and O. Tammelin. Heads-up limit hold’em poker is solved // Science. 2015. V. 347.

P. 145–149.

См. кроме этого:
А. В. Захаров «Теория игр в публичных науках» — хороший учебник по теории игр.

Дмитрий Дагаев