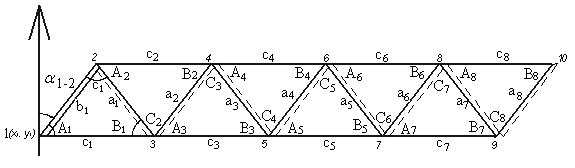
Содержание
Триангуляция
Потребность в измерении громадных, в сотни километров, расстояний – как на суше, так и на море – появилась ещё в древние времена. Метод триангуляции позволил высчитать огромные расстояния и определить фигуру Земли.
Понятие триангуляции
Пежде чем говорить о методе триангуляции, рассмотрим суть термина. Триангуляция — это сеть прилегающих друг к другу треугольников разного вида, можно сравнить с примыканием паркетин; наряду с этим существенно, что примыкают только целые стороны, так что вершина одного треугольника не может лежать внутри стороны другого. Триангуляции сыграли наиболее значимую роль в измерении расстояний на земной поверхности, и тем самым — и в определении фигуры Земли.
История измерения земных расстояний
Капитаны судов, как мы знаем из детских книг, меряют расстояния числом выкуренных трубок. Близок к этому метод, использовавшийся во II в. до н. э. известным древнегреческим философом, великим математиком и астрономом Посидонием, учителем Цицерона: морские расстояния Посидоний измерял длительностью плавания (с учётом, очевидно, скорости судна).
Но ещё раньше, в III веке до н. э., другой известный древний грек, управлявший библиотекой в Александрии великий математик и астроном Эратосфен, мерил сухопутные расстояния по времени и скорости движения торговых караванов. Возможно предположить, что именно так Эратосфен замерил расстояние между Сиеной и Александрией, которая в настоящее время называется Асуаном (если наблюдать по современной карте, получается приблизительно 850 км). Это расстояние было для него очень серьёзным. Эратосфен желал измерить длину меридиана и думал, что эти два египетских города лежат на одном и том же меридиане; не смотря на то, что это в конечном итоге не совсем так, но близко к истине. Найденное расстояние он принял за протяжённость дуги меридиана. Объединив эту длину с наблюдением полуденных высот Солнца над горизонтом в Сиене и Александрии, он потом путём красивых геометрических рассуждений вычислил протяжённость всего меридиана и, как следствие, радиус земного шара. Ещё в XVI веке расстояние (приблизительно 100 км) между Амьеном и Парижем определили подсчитав обороты колеса экипажа. Неточность результатов аналогичных измерений очевидна и объяснима. Но уже в следующем веке голландский математик, астроном и оптик Снеллиус смог изобрести принципиально новый, излагаемый ниже метод триангуляции и с его помощью в 1615–1617 гг. измерил дугу меридиана, имеющую угловой размер 1° 11′ 30″.
Суть метода триангуляции при измерении расстояний
Посмотрим, как триангуляция позволяет определять расстояния. Вначале выбирают какой-нибудь фрагмент или участок земной плоскости, включающий в себя оба пункта, расстояние между которыми стремятся найти, и доступный для проведения измерительных работ на местности. Данный участок покрывают сетью множества треугольников, образующих триангуляцию т. е. триангулируют. После этого выбирают один из треугольников триангуляции; будем называть его начальным. Потом выбирают одну из сторон начального треугольника. Она является базой, и её длину тщательно измеряют. В вершинах начального треугольника строят башни (или вышки) — с таким расчётом, чтобы каждая была видна с других башен. Поднявшись на башню, расположенную в одной из вершин базы, измеряют угол, под которым видны две другие башни. Затем поднимаются на башню, расположенную в другой вершине базы, и делают то же самое. Так, путем непосредственного измерения, получают сведения о длине одной из сторон начального треугольника (в частности: о длине базы) и о величине прилегающих к ней углов. По известным и простым формулам тригонометрии (с применением косинуса, синуса, тангенса и катангенса) вычисляют длины 2-х других сторон этого треугольника. Каждую из них можно принять за новую базу, причём измерять её длину уже не нужно. Используя ту же процедуру, возможно теперь определить длины сторон и углы любого из треугольников, примыкающих к начальному, и т. д. Важно осмыслить, что непосредственное измерение какого-либо расстояния выполняют лишь 1 раз, а дальше уже измеряют только углы между направлениями на башни, что несравненно легче и может быть сделано с высокой точностью. По завершении процесса оказываются установленными величины всех участвующих в триангуляции отрезков и углов. А это, в свою очередь, позволяет находить любые расстояния в пределах участка поверхности, покрытого триангуляцией.
Длина дуги меридиана от широты Северного Ледовитого океана до широты Чёрного моря
В частности, как раз так в XIX веке нашлась длина дуги меридиана от широты Северного Ледовитого океана (в районе Хaммерфеста на острове Квaлё – Норвегия) до широты Чёрного моря (в районе низовья Дуная). Она была сформирована из длин 12 отдельных дуг. Процедура упрощалась тем, что для нахождения длины дуги меридиана вовсе не нужно, чтобы составляющие дуги примыкали друг к другу концами; достаточно, чтобы концы соседних дуг находились на одной и той же широте. (К примеру, если необходимо определить расстояние между семидесятой и сороковой параллелями, то возможно на одном меридиане замерить расстояние между 70-й и 50-й параллелями, на другом меридиане — расстояние между 50-й и 40-й параллелями, а после этого сложить полученные расстояния.) Общее число треугольников триангуляции составило 258, длина дуги равнялась 2800 км. Чтобы исключить ошибки и неточности, неизбежные при измерениях, а при вычислениях вероятные, 10 подверглись прямому измерению на местности. Измерения были проведены в перид с 1816 по 1855 г.г., а итоги были изложены в двух томах «Дуга меридиана в 25° 20′ между Дунаем и Ледовитым морем» (СПб., 1856–1861), написанным замечательным русским геодезистом и астрономом Василием Яковлевичем Струве (1793–1864), осуществившего российскую часть измерений.
