Оригинальное доказательство теоремы Пифагора

Математик Андрес Навас из Университет де Сантьяго де Чили представил очередное простое и наглядное доказательство теоремы Пифагора. Посвященный изучению препринт создатель разместил на сайте arXiv.org.

Согласно теореме Пифагора в прямоугольном треугольнике квадрат гипотенузы равняется сумме квадратов катетов. В настоящее время известно более 350 доказательств этого утверждения.

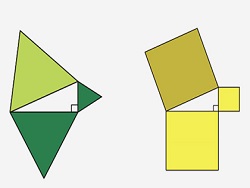
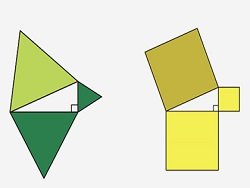
Навас применяет теорему Бойяи — Гервина, которая утверждает равносоставленность двух любых равновеликих многоугольников. Ученый выполняет два поворота треугольника “АВС” (на рисунке справа): первый — вокруг точки “А” на угол 60 градусов против часовой стрелки, второй — вокруг точки “В” на 60 градусов по часовой стрелке. После этого Навас рассчитывает площадь появившегося многоугольника, сформированного их двух многоугольников, площади которых равны площади треугольника “АВС”, и равностороннего треугольника со стороной с, откуда и выводит требуемое утверждение.

Теорема Пифагора, как утверждает в своей книге «Пробуждающаяся наука. Математика древнего Египта, Вавилона и Греции» нидерландский великий математик и историк науки Бартель ван дер Варден, была известна еще в восемнадцатом веке до н.э. обитателям Вавилона, и индийцам и египтянам. Известность она получила по окончании публикации 13 книг «Начал» Евклида, где в конце первой книги формулируется и доказывается теорема Пифагора.