Фракталы и хаос. Множество Мандельброта и другие чудеса – книга известного ученого математика Бенуа Мандельброта о хаосе в природе и составляющих его фрактальную структуру. То есть из небольших элементов состоят более крупные комплексы.
Теорию хаоса можно применить ко многим вещам во вселенной, к в том числе к государству и обществу в целом. А какую роль играет при этом фрактальная структура хаоса? Образ хаоса в пространстве ничто иное как фрактал.
Описание книги Фракталы и хаос
Год: 2009
Автор: Мандельброт Б.Б.
Переводчик: Зубченко Н.А.
Жанр: Математика
Издательство: НИЦ «Регулярная и хаотическая динамика» (Ижевск)
ISBN: 978-5-93972-772-3
Язык: Русский
Формат: DjVu
Качество: Отсканированные страницы
Интерактивное оглавление: Нет
Количество страниц: 386 (в книге 392)
Описание: Аннотация: «Немногим более двадцати лет минуло с тех пор, как Бенуа Мандельброт опубликовал свое знаменитое изображение так называемого множества Мандельброта. Эта картинка кардинально изменила наш взгляд на математическую и физическую Вселенную! Данная книга рассматривает не тот или иной класс проблем, а подход к описанию математической и физической Вселенной в целом. Фракталы (термин, придуманный автором) настолько прочно укоренились в нашем сознании, что сейчас крайне сложно вспомнить тот психологический шок, который мы испытали в момент их появления. Эта богато иллюстрированная книга объединяет ранние статьи автора, ставшие сегодня библиографической редкостью, с главами, описывающими историю развития фрактальной геометрии. Ключевые темы книги — квадратичная динамика, множества Жюлиа и Мандельброта, неквадратичная динамика, клейновы предельные множества и мера Минковского».
Примеры фракталов, динамических систем и хаоса
Деревья, как и многие другие объекты в природе, имеют фрактальное строение. Слева – фотография ели. Справа – искусственная фрактальная структура, генерируемая итерационными уравнениями.
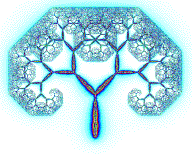По внешнему виду она очень напоминает живое дерево. Отчетливо видна структура ветвей, повторяющаяся во все более и более мелких масштабах.
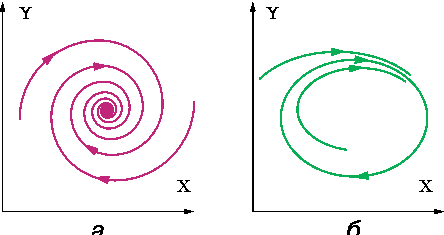
Движение динамической системы можно наглядно изобразить траекторией на фазовой плоскости, где оси X и Y – обобщенные координата и импульс частицы. а – колебания затухающего маятника. Траектории сходятся к одной точке, отвечающей положению равновесия – полной остановке маятника. б – периодические автоколебания. Все траектории ‘наматываются’ на предельный цикл – замкнутую кривую, соответствующую установившемуся процессу.
Примеры систем с хаосом. Когда две материальные точки отражаются от шариков, их траектории, первоначально близкие, быстро расходятся (слева). Причина неустойчивости – высокая чувствительность к начальным условиям, вызванная кривизной поверхности шариков. Справа – так называемый рассеивающий бильярд (бильярд Синая). Его криволинейные стенки выполняют ту же роль, что и система шаров слева.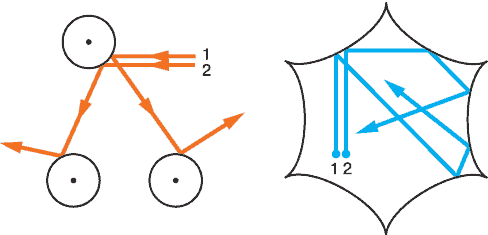
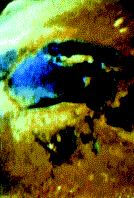
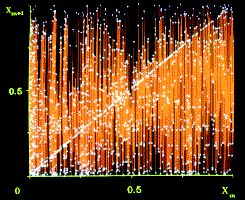
Пример записи информации с помощью детерминированного хаоса. Вверху – фотография Аральского моря, сделанная из космоса. Внизу – функция (оранжевым цветом), на которой записано оцифрованное изображение. Каждой белой точке соответствует несколько пикселов изображения.
Скачать книгу Фракталы и хаос. Множество Мандельброта и другие чудеса:
| Мандельброт Б.Б. – Фракталы и хаос – 2009 | 7.6 MB |
