
Пентамино — это фигура, составленная из пяти одинаковых квадратиков, соединенных сторонами. Существует 12 возможных форм пентамино, если не считать зеркально симметричные фигуры различными. Иногда их обозначают похожими буквами латинского алфавита. Кроме того, 12 —число шаров, которые могут одновременно касаться друг друга в трехмерном пространстве.
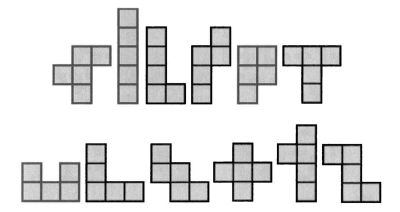
Полимино
В более общем смысле полимино — это фигура, составленная из η одинаковых квадратов. Все вместе эти фигуры называются полимино. Существует, к примеру, 35 гексамино (п = 6 ) и 108 гептамино (п = 7 ) .


Общую концепцию таких фигур, как и название, придумал Соломон Голомб в 1 9 5 3 г.; их популярности очень способ ствовали публикации Мартина Гарднера в Scientific American. Название образовано инверсно от слова «домино», костяшки которого состоят из двух соединенных квадратов; если исхи триться, то слог «до-» в названии игры можно интерпретировать как латинское di или греческое do, означающее «два». (На самом деле слово «домино» происходит от латинского dominus, «господин».)
Вообще, предшественников полимино в литературе хватает. Известный английский составитель головоломок Генри Дьюдени включил одну из головоломок с пентамино в свои «Кентерберийские головоломки» 1907 г. С 1937 по 1957 г. журнал Fairy Chess Review печатал много задач на складывание фигур из пентамино и гексамино, называя их «задачами на разрезание».
Головоломки с полимино
На полимино в целом и пентамино в частности основано громадное количество весьма занимательных игр и головоломок. К примеру, из них можно собирать различные интересные фигуры.
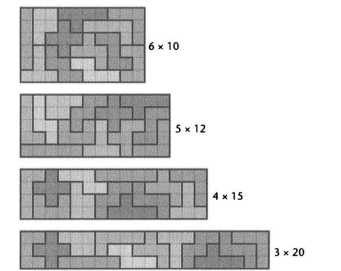
Площадь всех двенадцати пентамино в сумме составляет 60 единиц (если считать, что каждый квадрат, из которых составлены детали-пентамино, имеет площадь 1 ) . Любой способ записать 60 как произведение двух натуральных чисел определяет прямоугольник, и задача составления такого прямоугольника из деталей-пентамино представляет собой увлекательную и непростую головоломку. Детали при необходимости можно переворачивать, получая, таким образом, зеркальные фигуры. Оказывается, таким способом можно сложить прямо угольники 6 χ 10 , 5 χ 12 , 4 χ 15 и 3 χ 20 . Несложно убедиться, что прямоугольники 2 χ 30 и 1 χ 60 сложить невозможно.
Число различных способов сложить эти прямоугольники (поворот и отражение всего прямоугольника целиком не считаются как отдельные варианты, а вот поворот и отражение меньших прямоугольников, когда все остальное остается на месте, разрешается) известно:
6 χ 10 — 2339 способов;
5 x 12 — 1010 способов;
4 χ 15 — 368 способов;
3 χ 20 — 2 способа.
Еще одна типичная головоломка начинается с уравнения 8 x 8 – 2 x 2 = 60 и ставит вопрос: можно ли сложить из двенадцати пентамино квадрат 8 χ 8 с центральным отверстием 2 x 2 . Ответ: да, можно.

Симпатичный способ сложить все гексамино вместе дает параллелограмм :
Число полимино
Математики и компьютерщики рассчитали, сколько существует n-мино для многих n. Если не считать повороты и отражения отдельными фигурами, то общее число их таково:

Контактное число для шаров
Контактное число для кругов — наибольшее количество кругов, которые могут одновременно касаться данного, если все они одинакового размера — шесть. Существует также контактное число для шаров — наибольшее число шаров, которые могут касаться данного, если все они одинакового размера. Это число равно 1 2 . Показать, что 1 2 шаров могут одновременно касаться данного, довольно просто. Более того, можно сделать это таким образом, чтобы точки касания образовали 1 2 вершин правильного икосаэдра . Между этими точками достаточно места, чтобы поставить на каждое шар, и эти шары не будут касаться друг друга.
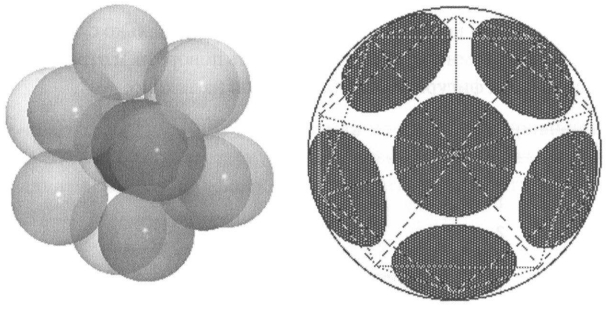
Справа: «тени» 12 шаров, касающихся данного шара в вершинах икосаэдра
На плоскости шесть кругов, одновременно касающиеся центрального, не оставляют свободного места, и вся конструкция получается жесткой. Но в трех измерениях свободного места остается немало, и шары можно двигать. Долгое время было неизвестно, не хватит ли этого свободного места для тринадцатого шара, если остальные двенадцать сдвинуть правильным образом. Два знаменитых математика — Ньютон и Дэвид Грегори — вели долгий спор по этому поводу. Ньютон утверждал, что правильное число 1 2 , тогда как Грегори был убежден, что оно должно быть 13 . В XIX в. предпринимались попытки доказать правоту Ньютона, но в них обнаруживались логические пробелы. Полное доказательство того, что контактное число для шаров главно 12 , было впервые опубликовано в 1953 г. Четыре измерения или больше Аналогичная ситуация возникает и в четырехмерном пространстве, где относительно несложно найти вариант одно временного касания 2 4 четырехмерных шаров, но остается достаточно места, чтобы туда, возможно, влез 25-й шар. В этом вопросе разобрался Олег Мусин в 2003 г.; ответ, как и ожидалось, составляет 24.
В большинстве других размерностей математики знают, что некоторое конкретное количество шаров может коснуться центрального шара, и они могут найти такое расположение шаров, при котором все получится; можно также сказать наверняка, что некоторое (как правило, значительно большее) число касаний невозможно, по различным косвенным признакам и причинам. Эти числа называются нижней и верхней границами контактного числа. Само число может лежать где-то между ними или равняться одной из границ.
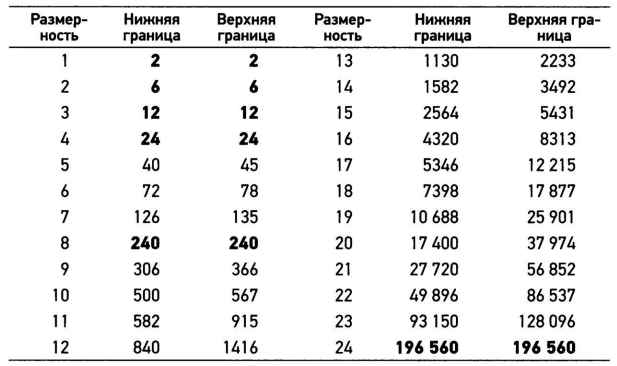
В двух случаях при размерностях больше 4 известные нижняя и верхняя границы совпадают, так что их общая величина и есть контактное число. Замечательно, что эти размерности 8 и 24 , для которых контактные числа составляют 240 и 196650 соответственно. В этих размерностях существует две высокосимметричные решетки — аналоги решеток из квадратов или, в более общем случае, из параллелограммов. Эти особые решетки известны как Е8 (или решетка Госсета) и решетка Лича, и шары можно разместить в подходящих для этого узловых точках. По едва ли не чудесному совпадению доказуемая верхняя граница контактного числа в этих измерениях совпадает с нижней границей, полученной при помощи этих особых решеток. Текущее состояние проблемы отражено в таблице, где полужирным выделены те размерности, для которых известен точный ответ:

Как читатель блога с категорией “Всё о математике”, пока я читал этот текст, возникли у меня несколько интересных вопросов
Мне тоже стало интересно, почему Ньютон и Грегори спорили о правильном числе.