
Содержание
- Введение в криптографию и криптовалюты
- Криптография в финансах
- Криптографические хэш-функции
- Хэш-указатели и стуктура данных
- Блок цепь (blockchain / block chain / блокчейн).
- Деревья Меркля
- Доказательство членства
- Доказательство не-членства
- Цифровые подписи
- Схема цифровой подписи
- 1-е свойство. Подпись должна подтверждаться
- 2-е свойство. Невозможность подделать (Unforgeability)
- Практические проблемы внедрения цифровой подписи
- Схема цифровой подписи ECDSA
- Публичные ключи как личности (англ: identities)
- Децентрализованное управление личностями
- Простейшая криптовлюта
- GoofyCoin
- ScroogeCoin
- Авторы
Введение в криптографию и криптовалюты
Статья технического характера по сути криптовалют, о методах защиты информации при транзакциях при помощи специальных алгоритмов.
Биткойн и криптовалюты и их добыча (майнинг) очень резонансные темы. Мы много слышали о стартапах, инвестициях, митапах и покупках пиццы за биткойны. Оптимисты верят, что биткойн коренным образом изменит международные платежи, экономику и даже политику. Пессимисты считают, что биткойн изначально ошибочен и криптовалюту ожидает неизбежный крах. В основе этих двух разных взглядов лежат заблуждения и путаница относительно понимания того, что такое биткойн и как это работает. Мы написали эту статью, чтобы помочь отделить зерна от плевел и добраться до самой сути криптовалюты, которая делает биткойн уникальным явлением.
Криптография в финансах
Любая валюта нуждается в определенном контроле и методах обеспечения безопасности, для предотвращения мошенничества. В случае с фиатными (традиционными) валютами, этим занимаются организации вроде центральных банков, которые контролируют деньги и разрабатывают средства защиты купюр и монет. Защитные знаки ставят определенный барьер для злоумышленников, однако, не гарантируют полную невозможность подделки денежных знаков. В конечном счете, правоохранительным органам необходимо предостерегать людей от правонарушений. Криптовалюты также нуждаются в средствах защиты, чтобы не позволить людям нарушить целостность системы и защититься от взаимоисключающих заявлений разных сторон. Например, если Алиса убеждает Боба, что она отправила ему монету, она не должна иметь возможности доказать Кэрол, что отправила ту же самую монету. Основная разница с фиатными валютами в том, что механизмы безопасности должны быть построены и основаны на технологиях, а не на влиянии властей. Как очевидно из названия, в основе криптовалют лежит криптография. С помощью криптографии обеспечиваются безопасность и правила шифрования в самой системе криптовалют. Это позволяет предотвратить фальсификацию монет и зашифровать правила эмиссии в математический алгоритм валюты. Поэтому, прежде чем мы сможем понять криптовалюты, нам придется ознакомиться с основами криптографии. Криптография сама по себе — огромное поле для академических исследований с использованием современных математических методов, которые, как известно, достаточно сложны для понимания. К счастью, биткойн основан на нескольких относительно простых и хорошо известных криптографических конструкциях. В этой главе мы будем изучать криптографические хэши и цифровые подписи — два примитива, которые доказали свою полезность при создании криптовалют.
Далее будут представлены более сложные криптографические схемы, к примеру — доказательство с нулевым разглашением, которое используется в предлагаемых расширениях и модификациях биткойна. После того как мы поняли всю важность криптографии, мы обсудим как она используется для создания криптовалют. В конце книги мы приведем примеры простых криптовалют, иллюстрирующих проектные задачи, с которыми придется иметь дело.
Криптографические хэш-функции
Первый криптографический примитив, который нам небходимо понять — это криптографические хэш-функции. Хэш-функция — это математическая функция, имеющая следующие свойства:
– Данные на входе могут быть любой строкой любого размера;
– На выходе данные имеют фиксированный размер. Чтобы конкретизировать обсуждения в данной главе, мы будем исходить из 256-битного размера данных на выходе. Однако все, что мы будем обсуждать, в равной степени применимо для любого размера выходных данных;
– Она эффективно вычислима. Это означает, что для заданной на входе строки данных, Вы можете вычислить, что вывод хэш-функции ограничен разумным количеством времени. Технически вычисление хэша n-битовой строки занимает время равное (n). Перечисленные свойства определяют общую хэш-функцию, которая может быть использована для структурирования данных, к примеру в виде хэш-таблицы. Мы будем рассматривать только криптографические хэш-функции. Для того, чтобы хэш-функция была криптографически стойкой, она должна удовлетворять следующим требованиям:
(1) стойкость к коллизиям первого рода или восстановлению вторых праобразов,
(2) необратимость или стойкость к восстановлению праобраза,
(3) стойкость к коллизиям второго рода.
ИЛИ (1) стойкость к коллизиям, (2) сокрытие, (3) дружелюбность к головоломкам.
Мы рассмотрим более подробно каждое из этих свойст, чтобы понять почему функция должна соответствовать данным требованиям. Читателю, знакомому с криптографией, следут знать, что представление о хэш-фунциях в этой книге, немного отличается от стандартного. К примеру, свойство дружелюбности к головоломкам не является основным требованием для хэш-функций, однако необходимо именно для криптовалют.
Свойство 1: Устойчивость к коллизиям. Первое свойство криптографических хэш-функиций, необходимое нам — это устойчивость к коллизиям. Коллизия возникает, когда два различных типа данных на входе порождают одни и те же данные на выходе.
Например, после шифрования строки А и строки Б мы получаем одни и те же данные.
Хэш-функция H(.) устойчива к коллизиям, если никто не может найти коллизию. Формально:
Устойчивость к коллизиям: Хэш-функция H считается устойчивой к коллизиям, если невозможно найти два значения x и y, при которых x ≠ y, а H(x)=H(y).

Обратите внимание, что мы использовали формулировку «никто не может найти коллизию», но это не подразумевает, что коллизии не существует в принципе. На самом деле мы знаем, что коллизия существует и можем доказать это с помощью простого алгоритма. Входное пространство хэш-функции содержит любые строки любой длинны, при том что на выходе данные содержатся в одной строке фиксированной длинны. Прежде всего потому, что данные на входе больше чем на выходе (пространство для ввода безгранично, в то время как на выходе ограничено), должны существовать строки ввода, которые отображают такую же строку выхода. В действительности, может существовать огромное количество вариантов исходных данных, которые на выходе дают одинаковый хэш.
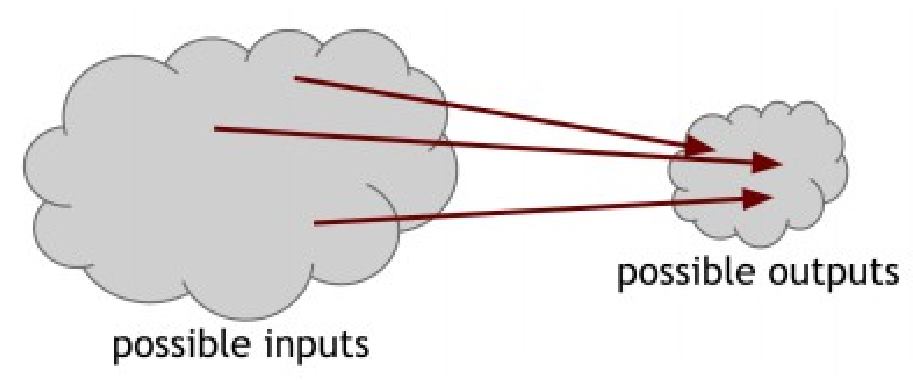
уверены, что существует по крайней мере 1 выход, при котором хэш-функция имеет более
чем 1 вариант входных данных.
Теперь ситуация усложняется и тем, что основным требованием к криптографической устойчивости хэш-функции, является невозможность найти коллизию. Тем не менее, существуют вполне гарантированные методы поиска коллизий. Рассмотрим один из простейших методов для поиска коллизий хэш-функции с 256-битным размером данных на выходе: возмем 2^256 + 1 различных значений и вычислим хэши каждого из них. После этого проверим существуют ли для них одинаковые значения на выходе. Так как мы выбрали больше входов, чем возможных выходов, примерно два из них должны быть одинаковы при применении хэш-функции. Используя метод приведенный выше достаточно просто найти коллизию. Но если мы будем использовать случайные входы и вычислять их хэши, поиск коллизий займет значительно больше времени. По факту, если мы случайным образом выберем только 2130 + 1 вход, вероятность того, что два из них будут давать на выходе один и тот же хэш равна 99,8%. Тот факт, что мы можем найти коллизии лишь рассматривая примерный квадратный корень из числа возможных выходов — результат феномена известного как «парадокс дня рождения». Этот алгоритм поиска коллизий работает для любой хэш-функции. Но основная проблема в том, что это занимает слишком много времени. Для хэш функции с 256-битным выходом вам потребуется вычислить хэш-функции 2256 степени +1 раз в худшем случае или около 2128 раз в среднем. Это конечно же астрономически огромные числа — если компьютер высчитывает порядка 10 000 хэшей в секунду, то весь процесс займет 1 миллион в восьмой степени лет, для подсчета 2128 хэшей. Другими словами, если каждый компьютер когда-либо изобретенный человечеством задействовать в этих вычислениях, шансы найти коллизию все еще останутся минимальными. Причем гораздо меньше чем шансы того, что Земля будет уничтожена гигантским метеоритов в следующие две секунды.
Таким образом мы имеем достаточно общеприменимый, но не практичный алгоритм поиска коллизий для любой хэш-функции. Гораздо более важный вопрос: существует ли какой-либо другой метод, который может быть применен к вполне конкретной хэш-функции для поиска коллизий? Другими словами, если общий алгоритм поиска коллизий не может быть использован, то все еще есть вариант применить другой, более эффективный алгоритм к конкретной хэш-функции. Для примера рассмотрим следующую хэш-функцию:
H(x) = x mod 2256 степени
Эта функция соответствует требованиям к хэш-функкции о том, что введенные данные любой длинны конвертируются в фиксированные данные на выходе (256 битов), кроме того, она эффективно вычислима. Но эта функция также имеет эффективный метод поиска коллизий. Обратите внимание, что эта функция просто возвращает последние 256-битов на входе. Одна коллизия будет иметь значение 3 и 3 +225. Этот простой пример иллюстрирует, что несмотря на то, что общий метод поиска коллизий плохоприменим, на практике, существуют определенные хэш-функции, для которых существует эффективный метод поиска коллизий.
Тем не менее, мы не знаем, существуют ли такие методы для других хэш-функций. Мы можем лишь подозревать, что они устойчивы к коллизиям. Как бы то ни было, не существует хэш-функций, которые бы доказали свою устойчивость к коллизиям. Криптографические хэш-функции, которые мы используем на практике, это всего-лишь такие функции, к которым люди пытались найти коллизии, но не смогли. И исходя из этого мы просто верим, что они устойчивы к коллизиям.
Применение: Исходя из вышесказанного, возникает логический вопрос: Для чего полезна устойчивость к коллизиям? Вот одно из возможных применений: Если мы знаем, что два входа x и y в устойчивой к коллизиям хэш-функции H имеют разные хэши, то разумно предположить, что x и y отличаются — если кто-то знает, что x и y различны, но имеют один хэш, то это разрушает наше представление о H как об устойчивой к коллизиям хэш-функции.
Этот аргумент позволяет нам использовать выходы хэшей как обзор сообщения. Рассмотрим SecureBox, онлайн-хранилище файлов позволяющее пользователям загружать файлы и быть уверенными в их неприкосновенности. Предположим, Алиса загружает действительно большой файл и хочет быть уверенна, что когда она будет его скачивать, файл будет именно тем файлом, который она загружала. Один из способов быть уверенным в этом — это сохранить этот большой файл локально и сопоставить его с файлом, который она будет скачивать. Хотя это и действительно рабочий метод, он исключает саму необходимость загрузки файла в хранилище. Действительно, зачем Алисе скачивать файл, который и так есть у нее на компьютере. Устойчивые к коллизиям хэши предоставляют простое и эффективное решение этой проблемы. Алисе достаточно просто запомнить хэш оригинального файла. И когда позже, ей понадобится скачать файл из SecureBox, ей достаточно будет сравнить его с хэшем скачиваемого файла. Если хэши совпадают, она может быть уверена, что это именно тот файл, который она загружала в хранилище.
В противном случае, когда хэши различны, Алиса может сделать вывод, что файл был изменен. Имея хэш оригинального файла, можно не только понять был ли он поврежден при загрузке в хранилище, но и не был ли он намеренно изменен посторонними. Так криптография может защищитить нас от злоумышленников.
Хэш служит своего рода дайджестом фиксированной длинны или резюмирующим сообщением. Это дает нам очень эффективный способ запоминания, распознавания и сопоставления вещей, событий и фактов. В то время как весь файл может весить несколько гигабайтов, хэш всегда имеет фиксированную длину, к примеру – 256-битов для хэш-фунции. Это в значительной степени решает проблему хранения данных. Позже в этой главе и на протяжении всей книги, мы столкнемся с приложениями, для которых хэши могут применяться в данном ключе.
Свойство 2: Сокрытие
Второе свойство, необходимое нам от хэш-функций — сокрытие. Это свойство позволяет нам быть уверенными, что для данных полученных на выходе хэш-функции y=H(x) нет способа просчитать какими были данные x на вводе. Проблема в том, что свойство не может быть правдой, в данной форме. Рассмотрим это на следующем примере: мы собираемся провести эксперимент с подбрасыванием монетки. Если монетка упадет орлом, мы скажем, что хэш строки — орел. Если монетка упадет вверх решкой, мы скажем, что хэш строки — решка.
После этого мы спросим нашего знакомого, который не видел результатов подбрасывания монетки, но видел хэши полученные в итоге, об исходных данных хэша. В ответ, наш знакомый может просто высчитать хэши строк «решка» и «орел» и буквально в два хода просчитать исходные данные хэша.
Противнику легко догадаться каким было значение строки, потому что существовало всего два возможных значения x и достаточно просто попробовать оба из них. Для того, чтобы достичь свойства сокрытия, необходимы условия, в которых нет вероятного значения х, к примеру, x должен быть выбран из набора условий, которые в некотором смысле достаточно распространены. Если x выбирается из такого набора, то этот метод перебора нескольких предположительных значений x, скорее всего не будет работать.
Серьезный вопрос: можем ли мы достичь свойства сокрытия, когда значение того, что мы не хотим подвергнуть огласке, установлено также как в экспертименте с монеткой? К счастью, ответ — да. Так мы можем скрыть вход не подвергнутый огласке сцепив его с другим входом, который будет оглашен. Теперь мы можем быть более уверенны в том, что подразумевается под скрытием (вертикальная черта | означает сцепление).
Сокрытие. Хэш-функция H скрытна, когда значение r выбрано из распределения вероятности которое имеет высокую минимальную энтропию, тогда при исходных H (r | x), невозможно найти x.
В теории информации минимальная энтропия является мерой того, насколько предсказуем результат, а высокая минимальная энтропия отражает интуитивное представление о том, что распределение (т. е. случайная величина) сильно распространится вовне. Это означает, что когда мы делаем выборку из распределения, то несуществует конкретного значения, которое может быть получено. Приведем более конкретный пример. Если r выбрано из единообразного набора всех строк длинной в 256 битов, то любая конкретная строка могла быть выбрана с ничтожно малой вероятностью в 1/2^256.
Применение: Обязательства. Теперь рассмотрим применение свойства сокрытия.В частности, то что мы собираемся сделать, называется обязательством. В цифровом плане, обязательство, это тоже самое, что принять определенное значение, запечатать его в конверт и положить этот конверт на стол, где его могут видеть все. Когда вы это делаете, то вы знаете, что лежит в конверте. Но вы не открываете конверт и даже не смотря на то, что вы знаете значение, оно по прежнему является секретом для всех остальных. Позже вы можете распечатать конверт и огласить обязательство взятое вами ранее.
Схема обязательств. Схема обязательств состоит из двух алгоритмов:
– (com, key) := commit(msg) – функция обязательства берет сообщение на входе и переводит их в два значения — обязательство и ключ.
– isValid := verify(com, key, msg) — функция проверки берет обязательство, ключ и сообщение как вводимые данные. Она возвращает положительный ответ, если com является верным обязательством к msg под ключем key. В пртивном случае функция возвращает негативный ответ.
При этом, обязательно соблюдение двух условий безопасного хранения:
– Скрытность: передача com не позволяет найти msg
– Привязка: для любого значения ключа невозможно найти два сообщения msg и msg’ таким образом msg ≠ msg’ и проверка (commit(msg), key, msg’) == верно.
Чтобы использовать схему обязательств, человек совершает значение и публикует обязательство com. Эта стадия аналогична тому, что вы кладете запечатанный конверт на стол. Позже, чтобы раскрыть взятые ранее обязательства, они публикуют ключ key и значение msg. После этого любой желающий сможет подтвердить, что msg соответствует условиям обязательств взятых ранее. Эта стадия аналогична вскрытию и огласке содержимого конверта.
Два свойства безопасности диктуют построение алгоритма подобно запечатке и открытию конверта. Первое com — данное обязательство, кто-то, кто смотрит на конверт не может понять в чем заключается сообщение. Второе свойство – это привязка. Это означает, что после принятия условий и запечатки конверта вы не можете изменить свои обязательства позже на другие.
Итак, как мы можем знать, что оба этих условия соблюдены? Прежде чем ответить на этот вопрос, мы должны поговорить о том, как мы собираемся внедрить схему обязательств. Мы можем сделать это используя криптографические хэш-функции. Рассмотрим следующую схему обязательств:
– обязательство(msg) := (H(key | msg), key) (где key — случайное 256-битное значение)
– проверка(com, key, msg) := верно, если H(key | msg) = com; в противном случае неверно.
В этой схеме, для совершения значения, мы генерирум случайное 256-битное значение, которое будет служить в качестве ключа. А после мы вернем значение ключа вместе с сообщением в качестве обязательства. Чтобы подтвердить, что никто не сгенерировал такой же хэш к ключу, они подаются вместе с сообщением. И это подтверждает является ли обязательство тем, чем оно было.
Посмотрим на эти свойства схемы обязательства по другому. Если мы подставим создание экземпляра обязательства и проверим как H (key | msg) для com, получатся следующие свойства:
– Сокрытие: Передан H(key | msg) невозможно найти msg
– Привязка: Для каждого значения ключа невозможно найти два сообщения msg и msg’ а значит msg ≠ msg’ и H(key | msg) = H(key|msg’)
Свойство сокрытия обязательств — это такое же свойство сокрытия, которое необходимо для наших хэш-функций. Key выбирается из случайного 256-битного значения и свойство сокрытия следовательно говорит, что если мы возьмем ключ и сопоставим его с сообщением, будет невозможно найти само сообщение. Из этого выясняется, что свойство привязки вытекает из свойства устойчивости к коллизиям, лежащего в основе хэш-функий. Если хэш- функция устойчива к коллизиям, то будет невозможно найти отличающиеся значения msg и
msg’ например в случае с H(key | msg) = H(key |msg’), поскольку эти значения будут являться коллизией.
Таким образом если H есть хэш-функция устойчивая к коллизиям и имеет привязку, эта схема обязательств будет работать с точки зрения соблюдения всех требований безопасности.
Свойство 3: Дружелюбность к головоломкам (puzzle-friendliness) . Третье свойство безопасности, необходимое хэш-функциям в том что они дружелюбны к головоломкам. Это свойство немного сложнее. Для начала мы объясним технические требования к этому свойству, а потом объясним почему оно полезно.
Дружелюбность к головоломкам. Хэш-функция H является дружелюбной к головоломкам если любое возможное n-бит выходное значение y, если k выбрано из распределения с высокой минимальной энтропией, тогда невозможно найти x как H(k | x) = y за время значительно меньше чем 2 в степени n.
Интуитивно, что это значит, если кто-то хочет получить хэш-функцию вполне определенного значения y на выходе, при том, что входные данные были выбраны случайным путем, то будет достаточно сложно найти другое такое значение, которое позволит достичь этой цели.
Применение: Головоломка поиск. Теперь давайте рассмотрим приложение, которое иллюстрирует полезность данного свойства. В этом приложении мы создадим головоломку поиск, математическую проблему которая требует поиска очень большого пространства для нахождения решения. В частности головоломка поиск не имеет ярлыков. Именно поэтому нет способа найти хоршее решение, кроме поиска большого пространства.
Головоломка поиск. Головоломка состоит из:
– хэш-функция H
– значение, id (которое мы называем ID головоломки), выбранное из распределения с высокой минимальной энтропией
– установленное в качестве цели Y Решением этой головоломки является значение x, как здесь: H(id | x) Y.∈
Интуитивно это так: если H имеет n-битное значение на выходе, то оно может принять любое из 2n значений. Решение головоломки подразумевает поиск введенных данных, которые на выходе будут находиться в пределах Y, который как правило значительно меньше чем множество всех решений (выходов).
Размер Y собственно определяет насколько сложна данная головоломка. Если Y – это набор всех n-битных строк, то головоломка достаточно тривиальна, в то время как если Y имеет только 1 значение, головоломка максимально усложняется. Факт в том, что id головоломки имеет высокую минимальную энтропию гарантирует отсутствие сокращений. Немного конкретней: если есть определенное значение ID, то кто-нибудь может сжульничать скажем, через предварительное решение головоломки с таким ID.
Если же головоломка puzzle-friendliness из этого следует, что нет стратегии по ее решению, которая подошла бы лучше, чем просто перебор случайных значений x. Таким образом, если мы хотим сделать головоломку трудно решаемой, то мы можем делать это так долго, как мы генерируем ID головоломки в случайном порядке. Мы применим эту идею позже, когда будем говорить о майнинге биткоина, который является своего рода вычислительной головоломкой.
SHA-256. Мы обсудили три свойства хэш-функций и по одному применению каждого из этих свойств. Теперь давайте поговорим о той хэш-функции, которую мы будем использовать в этой книге. Существует достаточно много хэш-функций, но одну из них биткоин использует в первую очередь и это хороший выбор. Она называется SHA-256.
Напомним, что наше требование к хэш-функциям — работа с выходами произвольной длины. К счастью, пока мы можем создать хэш-функцию которая работает с входами фиксированной длины, есть общий метод их конвертации в хэш-функцию, работающую с входами произвольной длины. Это называется структура Меркла-Дамгарда. SHA-256 — одна из нескольких обычно используемых функций, которые реализуют использование данного метода. В общей терминологии, основой фиксированной по размеру и устойчивой к коллизиям хэш-функций называется функция сжатия. Было доказано, что если основная функция сжатия устойчива к коллизиям, то и общая хэш-функция также устойчива к коллизиям.
Трансформация Меркла-Дамгарда очень проста. Скажем функция сжатия принимает вход длины m и выдает выход меньшей длины n. Вход хэш-функции, который может быть любого размера делится внутри блока на длину m-n. Конструкция работает следующим образом:
передать каждый блок совместно с выходными данными предыдущего блока в функции сжатия. Отметим, что длина выхода после этого будет (m-n)+n=m, что есть длина входа функции сжатия. Для первого блока, к которому нет выхода предыдущего блока мы используем вектор инициализации. Это число используется повторно для каждого вызова хэш-функции и на практике вы можете просто посмотреть его в стандартной документации. Последние выходные данные блока — результат к которому вы вернетесь. SHA-256 использует функцию сжатия, котрая принимает 768-битный вход, но на выходе дает 256-битную информацию. Размер блока 512 бит. Рассмотрим изображение 1.5, на котором визуализировано как работает SHA-256.
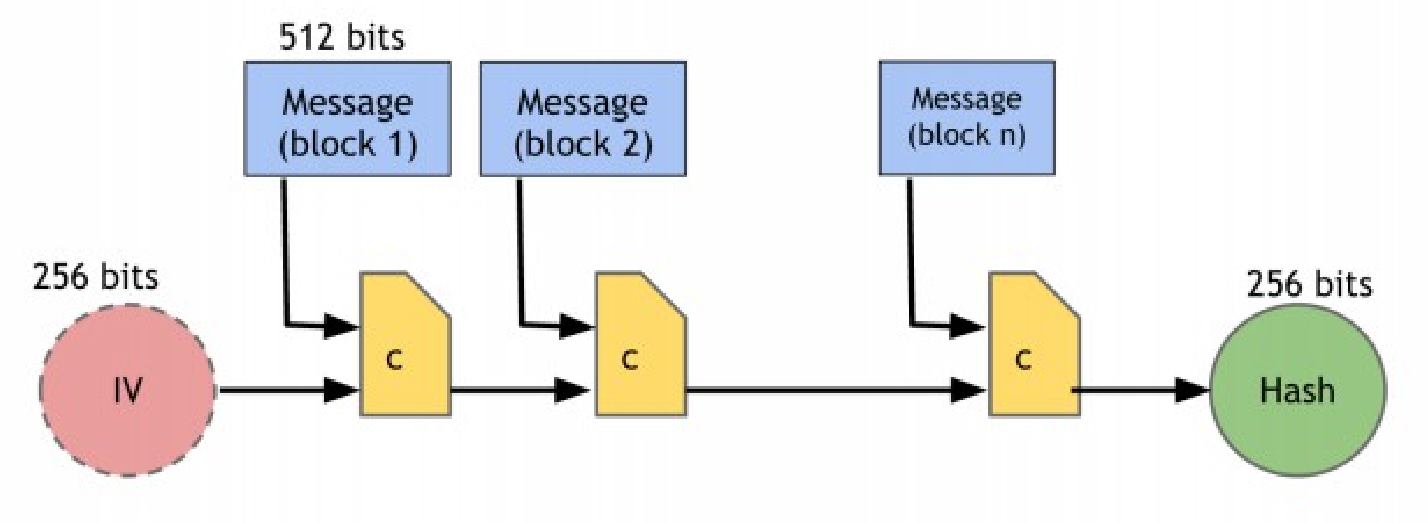
трансформацию Меркла-Дамгарда для включения устойчивой к коллизиям и
фикисированной по размеру функции сжатия в хэш-функцию, которая принимает на входе
данные произвольной длины.
Мы поговорили о хэш-функциях, криптографических хэш-функциях со специальными свойствами, применением этих свойств и хэш-функции используемой в биткойне. В следующем разделе мы обсудим пути использования хэш-функицй для построения более сложных структур данных, которые используются в распределенных системах вроде биткойна.
Хэш-указатели и стуктура данных
В этой части мы обсудим хэш-указатели и их применение. Хэш-указатели — это структуры данных, которые оказываются полезными во многи системах о которых пойдет речь. Хэш- указатели это простые указатели на место где какая-либо информация хранится совместно с криптографической хэш-информацией. В то время как обычный указатель позволяет вам просто получить информацию, хэш-указатель также позволяет вам убедиться в том, что информация не была изменена.
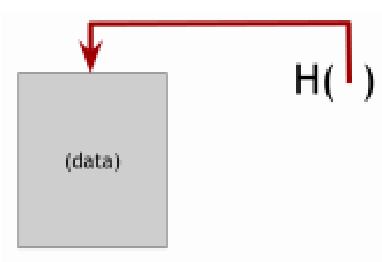
с криптографическим хэшем содержащим значение этих данных в определенный момент
времени.
Мы можем использовать хэш-указатели для построения любых структур данных. Теоретически мы можем взять известную нам структуру данных, которая использует указатели как структуру ссылок или дерево бинарного поиска и вместо привычного метода, реализовать ее через хэш-указатели.
Блок цепь (blockchain / block chain / блокчейн).
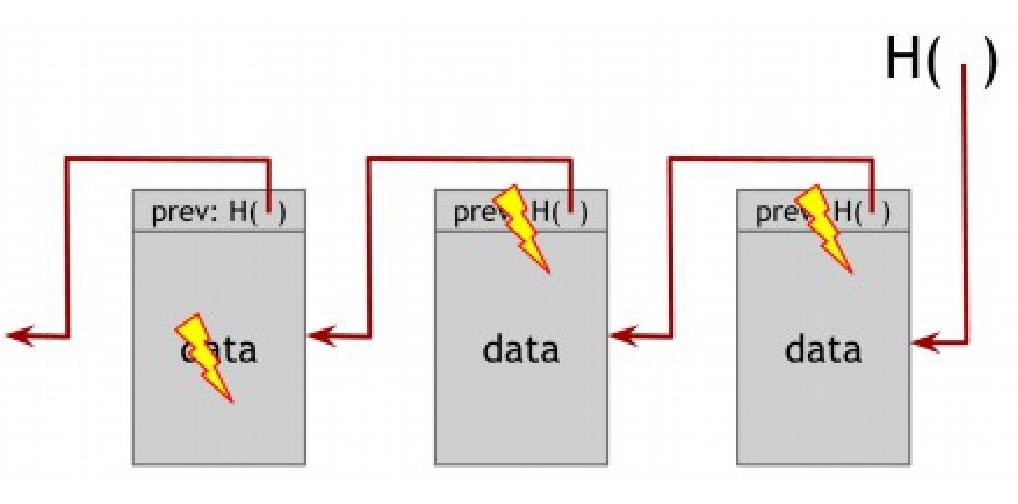
На рисунке 1.5 мы построили связанный ссылками список с использованием хэш-укзателей. Мы будем называть эти данные структурой блоковой цепи. В то время как в обычном связанном списке, где у вас есть серия блоков, каждый из которых содержит данные и указатель на предыдущий блок в списке, в блок цепи первый указатель блока будет заменен хэш-указателем. Таким образом каждый блок не просто показывает где находилось значение предыдущего блока, но также содержит дайджест значения предыдущего блока, что позволяет нам убедиться в целостности и неизменности данных. Мы храним лишь оглавление списка, которое является постоянным хэш-указателем на последний блок данных.
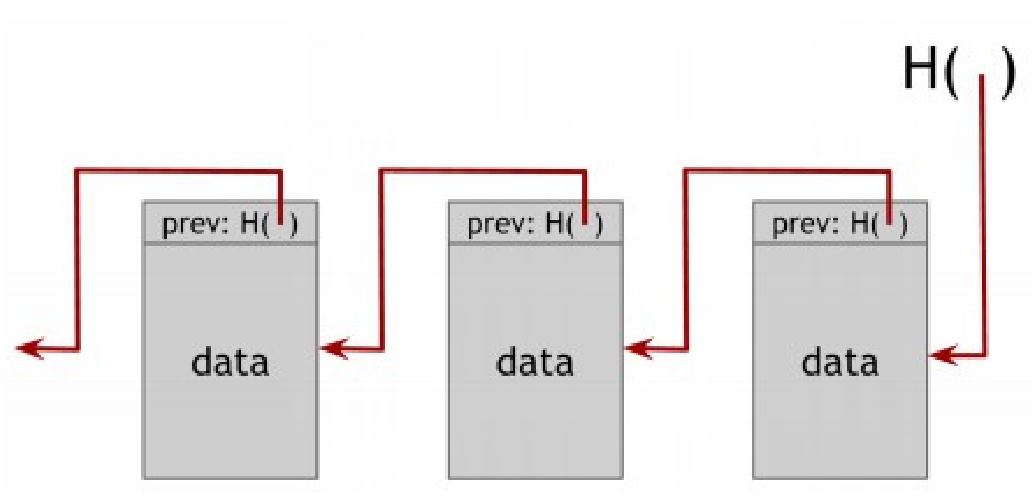
Примечание переводчиков: далее будет использоваться вариант перевода слова block chain – «блокчейн». Стоит обратить внимание, что зачастую под блокчейном и блокцепью может подразумеваться одно и то же. [англ.: block chain, blockchain]
Ипользуемый варинат для блокчейна — журнал несанкционированного доказательства (tamper-evident log). Это когда мы хотим построить журнал структуры данных, который хранит много информации и позволяет добавлять новые данные в конец журнала. Но если кто-то попытается изменить данные, добавленные в журнал ранее, мы узнаем об этом.
Чтобы понять почему блокчейн достигает этого свойства несанкционированного доказательства, давайте спросим, что случится, если кто-то захочет подделать данные находящиеся в середине цепочки. Цель злоумышленника в данном случае в том, чтобы сделать это таким образом, чтобы тот, кто помнит только хэш-указатель в заголовке блокчейна был не в состоянии обнаружить подмену.
Чтобы достичь этой цели, злоумышленник должен подменить данные в некотором блоке k. С того момента, как данные были изменены, хэш в блоке k+1, который является хэшем предыдущего блока k, более некорректен. Помните, что мы точно уверенны в том, что новый хэш не будет соответствовать другому содержимому, если хэш-функция устойчива к коллизиям.
Таким образом мы обнаружим несоответствие между новыми данными блока k и хэш- указателенм в блоке k+1. Конечно, противник, может попытаться скрыть эти изменения и подменить хэш следующего блока. Таким образом он может попытаться сделать это, но этот ход обречен на провал после достижения оглавления списка. В частности, пока мы храним хэш-указатели в оглавлении списка, там где противник не сможет их подменить, у него нет шансов внести изменения в блоки незаметно.
В результате, если противник хочет подменить данные в любом месте на протяжении всей цепочки блоков, для того, чтобы соблюсти последовательность, ему необходимо подменить хэш-указатели по всему блокчейну от начала до конца. И в конце-концов он застрянет на «блок посту», поскольку не сможет подменить данные в оглавлении списка. Таким образом, зная лишь один хэш-указатель мы в сущности имеем индикатор вскрытия – хэш существующего списка от начала и до конца. Таким образом мы можем построить блокчейн содержащий столько блоков, сколько мы хотим, вернувшись к одному специальному блоку в начале списка, который мы будем называть генезис блок (genesis block).
Вы можете заметить, что конструкция блокчейна очень похожа на структуру Меркля-Дамгарда, которую мы рассмотрели в предыдущей части. Они действительно мало чем отличаются и к ним применяется один и тот же аргумент безопасности.
Деревья Меркля
Другая полезная структура данных, которую мы можем построить используя хэш-указатели — это бинарное дерево. Бинарное дерево с хэш-указателями также называется дерево Меркля, в честь его изобретателя Ральфа Меркля. Предположим, что у нас есть некоторое количество блоков содержащих данные. Эти блоки содержат «листья» нашего дерева. Мы группируем эти блоки с данными по парам и после этого строим структуру данных, которая содержит два хэш-указателя по одному для каждого из блоков. Мы продолжаем строить структуру до тех пор, пока не достигнем последнего блока, который является корнем дерева.
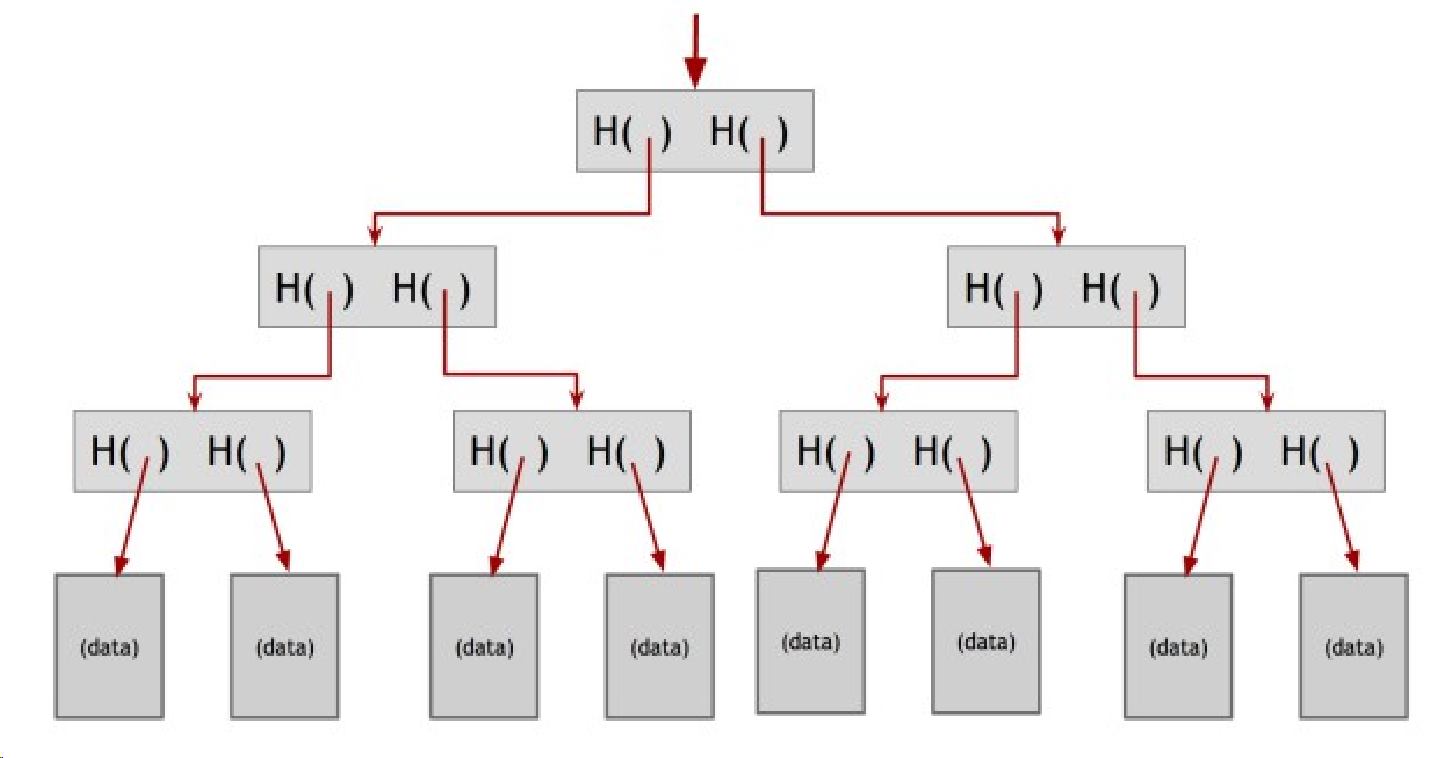
узлы также будут называться нодами). Родительские узлы в свою очередь также сгруппированы в парном порядке и их хэши хранятся на один уровень выше дерева. Это продолжается по всему дереву, пока мы не достигнем корневого узла.
Как и раньше мы запоминаем только хэш-указатель в оглавлении дерева. Теперь у нас есть возможность пройти вниз с помощью хэш-указателей в любую точку списка. Это позволяет нам быть уверенными, как мы расматривали это в случае с блокчейном, что данные не будут подделаны. Если злоумышленник подменит данные в одном из блоков внизу дерева, это по прежнему означает, что хэш-указатель на уровне выше будет некорректен. И даже если он продолжит подмену данных в каждом следующем блоке, изменения неизбежно приведут его к вершине дерева, где у него не будет возможности подделать хэш-указатель, который мы храним. Таким образом и здесь, любая попытка подмены данных может быть обнаружена с помощью основного хэш-указателя.
Доказательство членства
Доказательство членства (прим. пер.: анг – proof of membership). Другое хорошее свойство деревьев Меркля — это то, что в отличие от блокчейна который мы строили ранее, оно позволяет краткое доказательство членства. Предположим, кто-то хочет доказать, что конкретный блок данных является частью дерева Меркля. Как правило мы держим в памяти только корень. После этого он должен показать нам этот блок данных, а также блоки на пути от этого блока к корню. Мы можем игнорировать остальное дерево, поскольку этих блоков будет достаточно, для того чтобы мы могли сверить хэши на всем пути по дереву до корня.
Расмотрим рисунок 1.8, иллюстрирующий как это работает.
Если существует n узлов в дереве, только n количество пунктов журнала необходимо показать. А так как каждый шаг требует только подсчета хэша дочернего блока, проверка занимает n времени. И даже если дерево Меркля содержит слишком большое количество блоков, мы все еще можем доказать членство за относительно короткий промежуток времени. Проверка проходит во времени и пространстве, котрое логарифмично количеству нод в дереве.
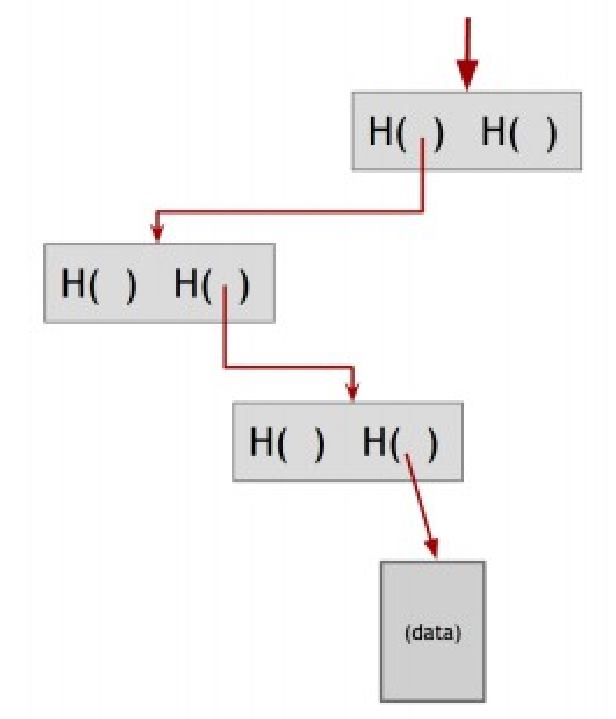
дерева, нам необходимо всего-лишь показать блоки на пути от этого блока к корню.
Отсортированное дерево Меркля — это дерево Меркля, в котором мы берем блоки внизу и сортируем их с использованием специальной функции упорядочивания. Это может быть алфавитный, лексикографический, числовой или любой другой согласованный метод упорядочивания.
Доказательство не-членства
В случае с отсортированным деревом Меркля становится возможно подтвердить не-членство в логарифмическом времени и пространстве. Таким образом мы можем доказать, что отдельный блок не находится в дереве Меркля. Делается это простым путем. Мы сравниваем с предъявленным блоком ту часть дерева, которая должна идти перед ним, а также ту часть которая должна идти после него. Если обе сопоставленные части дерева расположены последовательно, это доказывает, что предъявленный блок не был включен в основную цепочку. Ведь если бы он был включен, он должен располагаться между двумя сравниваемыми частями блокчейна, но так как они расположены последовательно, между ними нет пустого пространства.
И Мы уже обсуждали использование хэш-указателей в связанных списках и бинарных деревьях, но гораздо важнее, что мы можем использовать хэш-указатели в любой структуре данных до тех пор, пока эта структура данных не имеет циклов. Если в структуре данных существуют циклы, мы не сможем добиться совпадения всех хэшей. Если вы думаете об этом в нецикличной структуре данных, тогда мы можем начать рядом с листьями или рядом с вещами, которые не содержат никаких указаталей появившихся из них, и нам достаточно высчитать их хэши и затем работать по нашему пути к началу. Но в структуре без циклов нет конца от которого мы можем начать и высчитать возвращение. Итак, чтобы рассмотреть еще один пример, мы можем построить прямой нецикличный график из хэш-указателей. И мы будем иметь возможность подтвердить членство в этом графике достаточно эффективно. И это будет легко рассчитать. Использование хэш-указателей таким образом – это основной трюк, который вы будете встречать снова и снова в контексте распределенных структур данных, а также во всех алгоритмах, которые мы будем обсуждать в нашем цикле статей про блокчейн и криптовалюту.
Цифровые подписи
Это второй криптографический примитив наряду с хэш-функциями, которые необходимы для создания криптовалютных блоков. Цифровая подпись – это предполагаемый цифровой аналог рукописной подписи. Во-первых только вы можете сделать свою подпись, но любой, кто ее увидит, сможет подтвердить, что она корректна. Во-вторых мы хотим, чтобы подпись была привязана к конкретному документу, таким образом подпись может подтверждать ваше согласие или одобрение соответствующего документа. Для подписи сделанной от руки это свойство создает вероятность того, что кто-то может вырезать вашу подпись из одного документа и вклеить ее в другой.
Как мы можем создать подпись используя криптографию? Во-первых давайте немного конкретизируем обсуждение. Это позволит нам лучше понять схемы цифровых подписей и их свойства безопасности.
Схема цифровой подписи
Схема цифровой подписи состоит из следующих трех алгоримов:
– (sk, pk) := generateKeys(keysize) – метод generateKeys берет размер ключа и генерирует пару ключей. Секретный ключ sk хранится приватно и используется для подписи сообщений. Pk — это публичный ключ, который вы предоставляете всем. С помощью этого ключа любой может подтвердить вашу подпись.
– sig := sign(sk, message) — метод sign берет сообщение msg и приватный ключ sk как входные и выходные данные подписи для msg под sk.
– isValid := verify(pk, message, sig) – метод verify берет сообщение, подпись и публичный ключ как выходные данные. Он возвращает логическое значение isValid, которое будет верно, если sig является корректной подписью для сообщения под приватным ключом pk и неверно в обратном случае.
Нам обязательно соблюдение следующих свойств:
– корректная подпись должна подтверждать: verify (pk, message, sign(sk, message))=true;
– подписи экзистенциально неподдельны.
Отметим, что generateKeys и sign могут быть рандомизированными алгоритмами. Действительно, generateKeys имет более удачную рандомизацию (прим.пер.: подразумевается генерация случайного значения), потому что должен генерировать разные ключи для разных людей. Verify с другой стороны всегда будет детерменированным.
Теперь давайте рассмотрим свойства цифровых подписей более детально.
1-е свойство. Подпись должна подтверждаться
Первое свойство достаточно простое — верная подпись должна подтверждаться. Если я подписываю собщение через свой приватный ключ sk и позже, кто-то пытается подтвердить эту подпись под этим сообщением используя публичный ключ pk, подпись должна подтверждаться как корректная. Это свойство — базовое требование для использования цифровых подписей.
2-е свойство. Невозможность подделать (Unforgeability)
Невозможность подделать (Unforgeability). Второе требование — это невозможность подделки подписей. Это значит, что если некий злоумышленник знает ваш публичный ключ и может увидеть ваши подписи под другими сообщениями, он не может подделать вашу подпись под сообщением под которым вашей подписи нет. Это свойство невозможности подделки подписи, как правило формализовано условиями «игры» в которую мы играем со злоумышленником. Использование игр достаточно распространено при доказывании криптографической безопаности.
В игре о невозможности подделать существует противник, который утверждает, что сможет подделать подписи, а его соперник проверяет это утверждение. Певое что мы делаем — испольщуем generateKey для генерации приватного ключа и соответствующей открытой верификации. Мы даем приватный ключ стороне принимающей вызов и мы даем публичный ключ обеим сторонам игры, в том числе противнику. Таким образом противник (атакующий) знает только информацию из публичного ключа и его задача — попытаться подделать сообщение. Сторона принимающая вызов (атакуемый) знает приватный ключ и таким образом может делать подписи. Теоретически, условия этой игры соответствуют условиям реального мира. В реальной жизни атакующий будет видеть верные подписи своей потенциальной жертвы в разных документах. И возможно, он однажды сможет убедить жертву подписать безобидные на вид документы, если это будет в его интересах.
Чтобы смоделировать это в нашей игре, мы предоставим атакующему возможность получать подписи из разных докуменов по его выбору так долго, как он хочет, с учетом лимитированного количества предположений (догадок). Чтобы прояснить что мы имеем ввиду под числом возможных предположений, мы позволим атакующему сделать 1 миллион предположений, но не 2^80.
Когда атакующей будет считать, что видит достаточное количество подписей, тогда он выбирает несколько сообщений M, подпись под которые он попытается подделать. Единственное условие к M — это должно быть сообщение, для которого атакующий ранее не видел подписи (потому что атакующий может просто отправить обратно подпись, которую видел ранее!). Сторона принимающая вызов проходит алгоритм проверки, чтобы определить, что подпись произведенная жертвой действительно верна для M под публичным ключом. Если проверка проходит успешно, атакующий выигрывает игру.
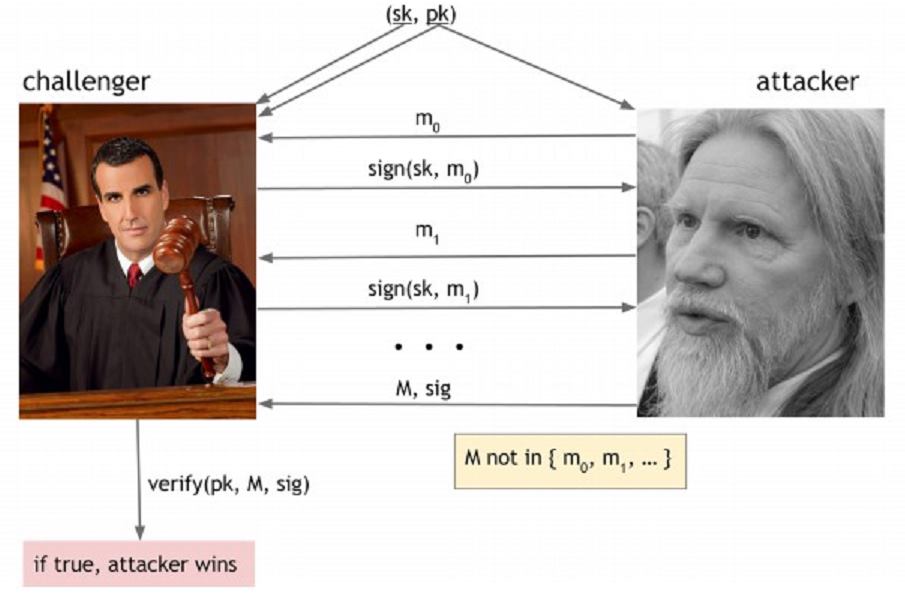
невозможность подделать. Если у атакующего получается подделать подпись на сообщение,
которое он ранее не видел, он побеждает. В противном случае — выигрывает атакуемый, а
схема цифровой подписи соответствует условию невозможности подделать.
Мы заявили, что подпись невозможна к подделке в том и лишь в том случае, если независимо от алгоритма, применяемого противником, его шанс удачно подделать сообщение ничтожно мал — настолько мал, что возможно высказать предположение, что этого не произойдёт никогда.
Практические проблемы внедрения цифровой подписи
Существует большое количество практических вещей, каковые нам нужно сделать, дабы включить идею алгоритма в механизм цифровых подписей, каковые смогут быть осуществлены на практике. Для примера, алгоритмы о которых мы говорили рандомизированы (по крайней мере кое-какие из них), из этого следует, что нам необходимы хорошие источники генерации случайностей. Важность этого не следует недооценивать, поскльку нехорошая рандомизация делает ваш алгоритм более уязвимым.
Другая практическая неприятность — размер сообщения. На практике существует ограничение размера сообщения, которое вы имеете возможность подписать, потому, что реально существующие схемы работают с битовыми строчками ограниченной длины. Существует простой метод обойти это ограничение: подписать хэш сообщения, а не само сообщение. Если мы используем криптографическую хэш-функцию с 256-битным выводом, значит мы можем действенно подписывать сообщение любой длины так долго, пока схема подписи может подписывать 256-битные сообщения. Как мы обсуждали ранее — это безопасно применять хэш сообщения в качестве дайджеста сообщения с того момента, как хэш-функция считается устойчивой к коллизиям.
Другой трюк, который мы будем применять позднее — это возможность подписывать хэш- указатель, так подпись скрывает или защищает всю структуру — не только сам хэш-указатель, но и все на что показывает цепочка хэш-указателей. К примеру, если вы подпишете хэш-указатель, который находится в конце блокчейна, вы в результате действенно подписали все входящее в данный блокчейн содержимое.
Схема цифровой подписи ECDSA
ECDSA. Сейчас давайте перейдем к деталям. Биткоин применяет конкретную схему цифровых подписей, которая называется Elliptic Curve Digital Signature Algorithm (ECDSA). ECDSA — это госстандарт в Соединенных Штатах. Мы не будем вдаваться в детали того как работает ECDSA, потому, что для этого нужно вдаваться в достаточно сложные математические подробности, каковые вовсе необязательны для понимания остального содержимого этого цикла статей.
В случае с ECDSA хорошая система генерации случайностей кроме этого крайне важна, потому, что плохой рандомайзер, вероятнее приведет к утечке ключа. Несложно понять, что если вы используете плохой рандомайзер при генераци ключа, это делает сгенерированнный вами ключ уязвимым. Но это особенность ECDSA, что если вы используете плохой рандомайзер лишь для создания подписи, ипользуя ваш самый хороший ключ, это кроме этого делает уязвимым ваш приватный ключ. И тогда игра окончена, поскольку если ваш приватный ключ был получен противником, он сможет подделать вашу подпись. Так мы должны быть предельно осторожны, применяя хороший рандомайзер, поскольку применение нехороших источников генерации случайности — это частая ошибка многих систем безопасности.
На этом мы завершим наш разговор о цифровых подписях как о криптографических примитивах. В следующей части мы обсудим прикладное использование цифровых подписей для разработки криптовалют.
Публичные ключи как личности (англ: identities)
Давайте рассмотрим замечательный трюк с применением цифровых подписей. Идея в том, дабы взять публичный ключ, один из публичных верификационных ключей в схеме цифровых подписей и приравнять его к личности человека или участника системы. Если вы видите сообщение с пописью, которая корректно подтверждается под публичным ключом pk, вы имеете возможность думать о нем как о pk говорящем сообщение. Вы имеете возможность относиться к pk как к участнику или группе в системе, каковые смогут делать какие-либо заявления непосредственно подписывая их. С данной точки зрения, публичный ключ — это личность. Чтобы кто-то выступал от имени pk, он должен знать соответствующий приватный ключ sk.
Следствием возможности обработки публичных ключей как личностей, есть то, что вы имеете возможность создать новую личность в любую секунду — достаточно просто создать новую несколько ключей sk и pk через оператор generateKeys в схеме цифровых подписей. Pk — это новая публичная личность, которую вы имеете возможность применять, а sk — это соответствующий приватный ключ, который понимаете лишь вы и который разрешает вам говорить от лица созданной личности. На практике вы имеете возможность применять хэш pk как личность потому, что публичные ключи велики.
Если вы делаете это, то чтобы убедиться, что сообщение исходит лично от вас, кто- то должн контролировать (1), что pk — это действительно хэши вашей личности и (2) сообщение подписано под публичным ключом pk. Более того, по умолчанию, ваш публичный ключ pk в основном выглядит случайным и никто не сможет раскрыть вашу настоящую личность анализируя pk. Вы имеете возможность генерировать новую личность которая выглядит случайным образом, которая выглядит как лицо в толпе и лишь вы имеете возможность это контролировать.
Децентрализованное управление личностями
Это приводит нас к идее децентрализованого управления личностями. Вместо того, дабы регистрировать себя как личность в системе через центральный орган власти, вы имеете возможность зарегистрироваться как пользователь самостоятельно. Вам не требуется получать логин специально или уведомлять кого-то о том, что вы станете применять именно это имя. Если вы желаете новую личность, вы просто генерируете ее в любое удобное для вас время. И вы имеете возможность делать это так часто, как вам хочется. Если вы предпочитаете быть известны за пятью различными именами — не неприятность. Просто сделайте пять личностей. Если вы желаете быть по каким-то обстоятельствам какое-то время полностью анонимным — никаких неприятностей, создайте особую личность, попользуйтесь ей и забудьте. Все эти вещи вероятны в децентрализованной системе управления личностями и это одновременно с этим путь по которому участники системы биткоин получают личности. Эти личности в биткоине называются адреса. Вы часто слышите термин адрес, в контексте биткоина и криптовалют, но все чем это в действительности есть — хэш публичного ключа. Это личность, которую кто-то создал из ничего и это часть схемы децентрализованной системы управления личностями.
Примечание. Идея того, что вы имеете возможность генерировать личность без центральной власти, может показаться нелогичной. Так как, к примеру, если кому-то очень сильно повезет и он сгенерирует такие же ключи, что и вы, разве не сможет он украсть ваши биткоины? Ответ в том, что возможность того, что кто-то сгенерирует такой же 256-битный ключ как и вы, настолько мала, что не следует тревожиться об этом действительно. Мы со всей уверенностью гарантируем, что этого не произойдёт никогда.
Более конкретно, в отличие от мнения начинающих, что система непредсказуема и весьма сложно строить какие-либо предположения, зачастую все наоборот — теория статистики разрешает нам установить точную возможность того или иного события и сделать обоснованные утверждения о поведении таких систем.
Но есть тонкость: вероятностная гарантия верна лишь тогда, в то время, когда ключи генерируются случайным образом. Генерация случайностей часто есть уязвимым местом настоящих систем. Если два пользователя компьютера применяют один и тот же источник случайностей или применяют предсказуемые случайности, тогда теоретические гарантии больше не работают. Так важно применять хорошие источники случайностей при генерации ключей, дабы практические гарантии соответствовали теоретическим. На первый взгляд может показаться, что децентрализованная система управления личностями приводит к большей анонимности и безопасности. Так как вы имеете возможность создать любую личность самостоятельно и наряду с этим не требуется никому собщать свои настоящие данные. Но все не так просто. Со временем, личность, которую вы создаете, делает серию заявлений. Люди видят эти заявления и знают, что кто-то, кто стоит за данной личностью сделал череду определенных действий. Они смогут начать соединять точки, применяя ваши действия, дабы установить вашу личность в реальности. Наблюдатель может связывать все эти вещи воедино весьма долго и делать определенные умозаключения, к примеру «Ну и дела, данный чувак такой же деятельный, как Джо. Возможно он и есть Джо?».
Иначе говоря в Биткоине вы не должны явно регистрировать или раскрывать свои персональные данные, но паттерны вашего поведения смогут выдать вас.
Простейшая криптовлюта
Сейчас давайте перейдем от криптографии к криптовалютам. Все что мы изучили о криптографии ранее, понадобится нам с этого момента. И мы постепенно увидим как различные части начинают взаимодействовать совместно и из-за чего криптографические операции вроде хэш- функций и цифровых подписей действительно серьёзны. В данной части мы обсудим две весьма простые криптовалюты. А в дальнейшем нам пригодится большое количество времени, дабы объяснить, как работает биткоин.
GoofyCoin
Первая из этих двух криптовалют — GoofyCoin, она есть простейшей криптовалютой, которую возможно себе представить. В GoofyCoin есть всего два правила. Первое правило в том, что назначенный субъект может быть создать новые монеты в любую секунду, в то время, когда он захочет и эти снова созданные монеты принадлежат ему. Дабы создать монету, Goofy генерирует уникальный ID монеты uniqueCoinID, который ранее до этого не был сгенерирован и состоит из строки CreateCoin [uniqueCoinID]. Затем он вычисляет цифровую подпись данной строки с ее приватным ключом подписи. Строка, вместе с подписью Goofy — это и есть монета. Любой может подтвердить, что эта монета содержит валидную подпись Goofy исходя из сообщения CreateCoin и исходя из этого монета будет действительной.
Второе правило GoofyCoin содержится в том, что тот, кто владеет монетой может передать ее кому-либо еще. Отправка монеты это не просто операция по отправке структуры данных монеты получателю, это делается с применением криптографических операций. Давайте предположим, что Goofy желает послать созданную им монету Алисе. Дабы сделать это, он формирует новое собщение, где говорится «Заплати это Алисе», где «это» – хэш указатель, который ссылается на монету. И как мы видели ранее, личности — это всего-лишь публичные ключи, значит «Алиса» отсылает к публичному ключу Алисы. В итоге, Goofy подписывает сообщение. Так, Goofy, который есть изначальным владельцем монеты, путем подписи транзакции израсходовал эту монету. По окончании того, как структура данных представленная в транзакции Goofy подписана им, Алиса делается владельцем данной монеты. Она может доказать любому, что владеет данной монетой, потому что она может продемонстрировать структуру данных, с валидной подписью Goofy. Помимо этого, она показывает на монету, которой владел Goofy. Так валидность и право собственности на монеты безопасно-очевидны в данной системе.
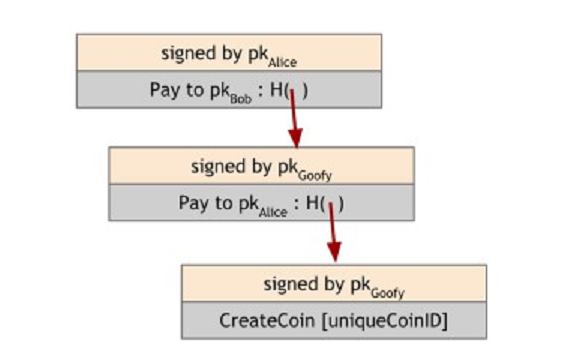
дважды (середина и верх). Раз Алиса владеет монетой, она, в свою очередь, может потратить
ее. Чтобы сделать это, она делает заявление, в котором говорит «Заплатить эту монету
публичному ключу Боба», где «это» – хэш-указатель на монету, которой она владеет. И
конечно, Алиса подписывает свое заявление. Любой, кто столкнется с этой монетой сможет
подтвердить, что Боб ее владелец. Желающие убедиться в этом будут следовать за цепочкой
хэш-указателей назад, к моменту создания монеты и будут получать подтверждение
правомерность владения шаг за шагом.
Суммируем правила GoofyCoin:
– Goofy может создать новые монеты простой подписью заявления о том, что он формирует новую монету с уникальным Id.
– Тот, кто владеет монетой, может послать ее кому угодно, подписав заявление в котором информирует: «Передать эту монету к X» (где X — особый публичный ключ).
– Любой может подтвердить валидность монеты, следуя за цепочкой хэш-указателей к моменту создания монеты Goofy. Наряду с этим он будет получать подтверждения всех подписей в течении всего цикла проверки.
Само собой разумеется, в GoofyCoin есть фундаментальная неприятность безопасности. Скажем, Алиса передала свою монету Бобу через подпись заявления к Бобу, но больше не сказала об этом никому. Она может создать другое подписанное заявление, которое будет передавать ту же самую монету Чаку. Для Чака это будет означать, что это совсем валидная транзакция и сейчас он владелец монеты. Боб и Чак оба будут иметь действительные на вид права владения монетой. Это называется дабл-спенд атака (прим.пер: потом – атака двойной
траты) — Алиса тратит одну и ту же монету два раза. Мы знаем, что монеты не должны работать так.
По факту, атака двойной траты— ключевая пробема, которая обязана решаться в любой криптовалюте. GoofyCoin не решает проблему атаки двойной траты и исходя из этого есть незащищенной. GoofyCoin — весьма простая и механизм отправки монет весьма похож на биткоин, но из-за своей незащищенности, она не имеет возможности соперничать с ним, как криптовалюта.
ScroogeCoin
Дабы решить проблему двойной траты, мы создадим другую криптовалюту, которую назовем ScroogeCoin. Мы создадим ее на подобие GoofyCoin, но немного сложнее в плане структуры данных.
Первая ключевая идея в том, что назначенный объект, называемый Scrooge публикует всю историю всех транзакций, каковые когда-либо произошли. Для этого он применяет блокчейн (структуру данных, которую мы обсуждали ранее), которую Scrooge подписывает цифровым образом. Это серия блоков данных, каждый из которых содержит одну транзакцию (на практике, для оптимизации мы можем пометистить пара транзакций в один и тот же блок, как это делается в биткоине). Каждый блок содержит ID транзакции, содержимое транзакции и хэш-указатель на прошлый блок. Scrooge цифровой подписью подписывает финальный хэш-указатель, который представляет всю эту структуру и публикует подпись вместе с блокчейном.
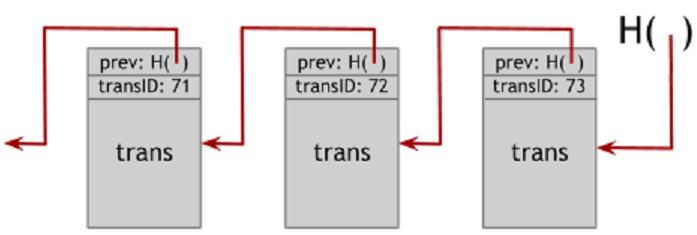
В ScroogeCoin транзакции засчитываются лишь если они подписаны в блокчейн Scrooge. Любой может проверить, что транзакция одобрена Scrooge проверив его подпись на блоке, в котором находится транзакция. Scrooge дает гарантии, что он не подпишет транзакцию, при помощи которой пробуют израсходовать одну и ту же монету два раза.
Для чего нам нужен блокчейн с хэш-указателями в дополнение к тому, что Scrooge подписывает каждый блок? Блокчейн предотвращает возможность того, что Scrooge в какой-то момент захочет поменять историю транзакций. Если он захочет добавить или удалить транзакцию из истории, или поменять существующую транзакцию, это скажется на всех блоках, по причине наличия хэш-указателей. До тех пор пока кто-то следит за последними хэш-указателями, опубликованными Scrooge, изменение будет очивидно и подметить его будет легко. В системе, где Scrooge подписывает блоки самостоятельно, вам нужно следить за каждой отдельной подписью, когда-либо сделанной Scrooge. Блокчейн делает это весьма простым процессом для любых двух людей, каковые подтверждают тот факт, что они замечали такую же историю транзакций, что подписал Scrooge.
В ScroogeCoin существует два типа транзакций. Первый тип — это CreateCoins (создание монет), который как и операция Goofy в GoofyCoin формирует новую монету. В ScroogeCoin мы немного расширили семантику, дабы разрешить создавать пара монет за одну транзакцию.
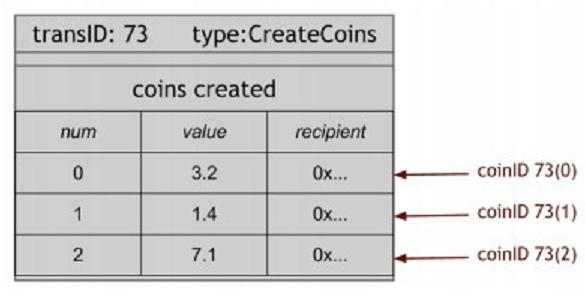
Эта транзакция формирует пара монет. Каждая монета в транзакции имеет серийный номер. Кроме этого каждая монета имеет ценность; она стоит определенное количество ScroogeCoins. В итоге, у каждой монеты есть получатель, который есть публичным ключом, получающим монету, по окончании ее создания. Так CreateCoin формирует определенное количество новых монет различного номинала и присваивает их определенным людям в качестве изначальных владельцев. Мы ссылаемся на монеты по CoinID. CoinID – это комбинация из ID транзакции и серийного номера монеты в данной транзакции.
Транзакция CreateCoins неизменно по определению валидна, если она подписана Scrooge. Мы можем не тревожиться о том, в то время, когда Scooge формирует монеты или как много, кроме этого как мы не волнуемся в GoofyCoin о том, как Goofy решил создать монеты. Второй тип транзакции — PayCoins. Она потребляет пара монет, уничтожая их и создавая новые монеты того же номинала. Новые монеты смогут принадлежать различным людям (публичным ключам). Эта транзакция должна быть подписана всеми, кто платит монеты. Так, если вы владелец монет, каковые будут потребляться в данной транзакции, вы должны цифровым образом подписать транзакцию, дабы подтвердить свое согласие на трату монет.
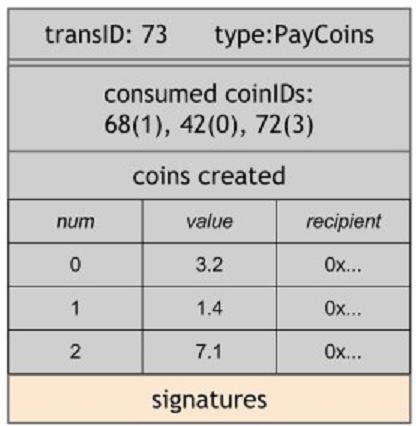
В соответствии с правилам ScroogeCoin, транзакция валидна, если соблюдаются четыре правила:
– Потребляемые монеты валидны, если они действительно были созданы в предыдущей транзакции.
– Потребляемые монеты не являются уже потребленными в одной из прошлых транзакций. Это подтверждает тот факт, что не происходит двойной траты.
– Общий номинал монет, полученных из данной транзакции эквивалентен общему номиналу монет, каковые были задействованы в ней изначально. Это вследствие того что лишь Scrooge может создавать новые ценности.
– Транзакция действительно подписана владельцами всех потребляемых монет.
Если все эти условия соблюдены, значит транзакция PayCoin валидна и Scrooge акцептирует ее. Он запишет ее в историю, добавив ее в блокчейн по окончании чего любой сможет разглядеть, что транзакция произошла. Это единственная точка, в которой участники смогут понять, что транзакция произошла. , пока она не опубликована, она возможно вытеснена транзакцией двойной траты, кроме того если она соответствует первым трем условиям валидности транзакций.
Монеты в данной системе неизменны — они никогда не изменяются, не разделяются и не комбинируются. Каждая монета создается лишь один раз в одной транзакции и позднее возможно израсходована в другой транзакции. Но мы можем добиться того же результата, как разделение или комбинирование монет, применяя транзакцию. Для примера — разделение монет. Алиса формирует новую транзакцию, которая расходует одну монету, по окончании чего производит две новые монеты, в сумме эквивалентные изначальной монете. Эти две монеты в свою очередь смогут быть присвоены ей. Так, без оглядки на то, что монеты являются неизменными в данной системе, она имеет всю гибкость системы, которой не имеют неизменные монеты.
Сейчас мы перейдем к проблемам ядра ScroogeCoin. ScroogeCoin работает в том смысле, что люди смогут видеть какая монета есть валидной. Это защищает от двойных трат, потому что каждый может взглянуть в блокчейн и увидеть, что все транзакции валидны и все монеты израсходованы лишь один раз. Но неприятность в самом Scrooge — он имеет через чур много влияния. Он не имеет возможности создать поддельные транзакции, потому что не сможет подделать подписи других людей. Но он может прекратить одобрять транзакции от некоторых пользователей, отказывая им в обслуживании и тем самым делая невозможной трату их монет. Если Scrooge жадный (на что показывает имя персонажа мультфильма), он может отказаться публиковать транзакции , пока с каждой транзакции ему не будет уплачена некоторая рабочая группа. Кроме этого Scrooge, конечно же, может создать для себя столько новых монет, сколько он захочет. Или же ему вовсе надоест заниматься все данной системой и он прекратит обновлять блокчейн.
Ключевая неприятность в централизации. Не смотря на то, что Scrooge счастлив с данной системой, мы как ее пользователи — не можем поделить его радости. Пока ScroogeCoin может смотреться как нереальное предложение, большинство ранних изучений криптосистем предполагало, что они будут нуждаться в чем то вроде доверенного центра (в большинстве случаев государственный монетный двор), важный за создание валюты и определение какие конкретно записи являются валидными. Как бы то ни было, криптовалюты с центральным авторитетом, на практике не имели успеха. Существует большое количество обстоятельств из-за чего, но в ретроспективе думается, что это достатчно тяжело убедить людей принять криптвалюту с центральным органом власти.
Так ключевой технической задачей, которую мы должны решить чтобы улучшить ScroogeCoin и создать работоспособную систему: можем ли мы децентрализовать систему? В частности, можем ли мы избавиться от центрального органа в виде Scrooge? Можем ли мы иметь криптовалюту, работающую во многом как Scroogecoin, но не имеющую центрального органа управления. Дабы сделать это, нам необходимо придумать, как все пользователи могли бы дать согласие с единым блокчейном, в котором будут записываться всепроисходящие транзакции. Все они должны найти консенсус по вопросу того, какие конкретно транзакции считаются валидными, и какие конкретно сделки в действительности произошли.
Они кроме этого должны имеь возможность назначать ID вещей в децентрализованном порядке. В конечном счете, чеканка новых монет обязана контролироваться в децентрализованном порядке. Если мы можем решить все эти неприятности, значит мы сможем создать валюту, которая будет подобна ScroogeCoin, но не будет централизованной. По факту это будет система весьма похожая на биткойн.
Авторы
Биткойн и криптовалютные технологии. Авторы и составители Arvind Narayanan Joseph Bonneau Edward Felten Andrew Miller Steven Goldfeder Draft Январь, 2015
Перевод ForkLog.com Редакция №1 (июль 2015)
.
