Интересные факты о происхождении чисел

Приблизительно три с половиной тысячи лет тому назад,  в верхнем  палеолите,  неведомый человек вырезал 29 зарубок на малой берцовой косточке павиана. Косточка эта была раскопана в пещере в высотах Лебомбо, находящимся в Свази­ленде, а оттого так и именуется — «кость из Лебомбо». Счи­тается, что это счетная бирка — вещь, на которой  записыва­ют цифры (числа) в виде партии зарубок:  |,  ||,  |||  и без того потом. В лунном месяце  29,5  дней, так что это возможно незамысловатый лун­ный календарь — либо запись дамского месячного цикла. 
Либо, по большому счету говоря, случайный комплект вырезов. Экие кара­кули на кости. 
Еще одну счетную пластинку или бирку с 55 обозначениями, В этом случае на вол­чьей кости, отыскал в Чехословакии в  1937 г. Карел Абсолон. Ее возраст приблизительно три тысячи  лет. 
В 1960 г. бельгийский геолог Жан Эйнзелен де Брокур обна­ружил еще одну маленькую  берцовую кость павиана  с зарубками среди остатков маленькой рыбацкой деревушки, попавшей под извержение вулкана и захороненной под слоем пепла. Сто­янка  рыбаков  размешалась  в нынешнем  Ишанго,  районе на границе Уганды и  Конго. Возраст  останков —  приблизительно 20000  лет. Несложное  объяснение  кости  из  Ишанго  —  это снова же счетная  бирка. Одни антропологи  идут еще дальше и открывают в ней звенья  цифирной  структуры,  такие как  умножение,  простые  числа  и  деление;  другие  находят, что это шестимесячный лунный календарь; третьи же убежде­ны,  что зарубки  на кости  созданы чтобы  костяное приспособление было эргономичнее держать в руке, и что в нем нет ника­кого математического смысла.
 

Находка, непременно, интригующая. На кости есть  3 серии насечек. В центральной серии находятся числа  3, 6, 4 , 8, 10 , 5, 7. Два раза три — 6 , два раза  четыре — 8, а дваж­ды  пять  —  10 ;  но  последняя  пара  чисел  находится в обратном порядке, а 7 по большому счету никак не укладывается в схе­му. В левой серии находятся группы по  11 , 13 , 17 , 19  насе­чек; это простые числа в промежутке от  10 до  20 .  Правая серия дает нам нечетные числа  11 , 21 ,  19 ,  9 . Сумма чисел как в пра­вой, так и в левой части равна  60 . Неприятность  с  интерпретацией  аналогичных  образцов  пребывает в том, что в любой  серии  не  через чур  солидных чисел  тяжело не отыскать никаких закономерностей.  К примеру, в табл. 1 приведены площади десяти островов Багамского архипелага, занима­ющих места с 11-го по 20-е по площади среди всех островов. Что­бы внесли дополнительный элемент случайности, я разместил их в алфавитном порядке. Поверьте, это было первое, что при­шло мне в голову. Соглашусь, что я сменил бы их чем-нибудь иным, если бы эти числа не оправдали моих надежд, но они оправдали — и мне не привелось ничего изменять. 
Итак, какие конкретно «закономерности» возможно увидеть в этом набо­ре чисел? В том месте множество маленьких последовательностей чисел, владеющих неспециализированными чертами. 
 

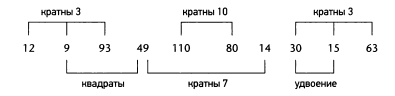
Для начала: весь перечень оказался поразительно симметричным. С каждой стороны находится по 3 числа, делящихся на три.  В сере­дине имеется пара чисел, кратных  10 , по бокам от которых сто­ят два числа, кратные  7. Более того, имеют место два квадрата: 9  = З2  и 49  =  72 ; то и второе — квадрат несложного числа. Еще одна соседняя пара —  15  и  30 ;  одно из чисел в два раза больше другого. В последовательности  9 – 93 – 49  в каждом из чисел имеется цифра 9. Каждое следующее число то больше, то меньше пре­дыдущего, за исключением цепочки  110 – 80 – 14 . Да, и вы замети­ли,  что среди этих десяти чисел нет ни одного несложного? Сообщённого достаточно. Еще одна неприятность с костью из Ишан­го пребывает в том, что отыскать какие конкретно бы то ни было дополнитель­ные данные в пользу любой конкретной интерпретации насечек фактически нереально. Несомненно, история очень интригу­ющая. Числовые головоломки постоянно производят завораживаю­щее чувство. Так что приведем менее сомнительный пример. 
 

Таблица 1

Название	Площадь в квадратных  милях
Берри	12
Бимини	9
Крунед-Айленд	93
Малый  Инагуа	49
Маягуана	110
Нью-Провиденс	80
Рэггид-Айленд	14
Рам-Ки	30
Самана-Ки	15
Сан-Сальвадор	63

10000 лет тому  назад  на  Ближнем  Востоке  для  запи­си чисел употреблялись  особые  керамические бирки; чис­ла эти, вероятнее, были связаны с налогообложением  либо, может  быть,  удостоверяли  право  владения.  Самые  древние бирки отысканы при раскопках тепе (холмов) Асьяб и Гандж-и-
Дарех — двух археологических  монументов  в иранских  горах Загрос. Бирки представляли собой маленькие комочки глины различной  формы,  кое-какие  из них отмечены  определенными знаками. Считается, что шарик со знаком + обозначал одну овцу; семь таких шариков, соответственно,  обозначали  семь овец. Дабы не делать через чур много шариков, имелись бир­ки второй формы, обозначавшие сходу десять овец. Были спе­циальные бирки для десяти коз и без того потом. Археолог Дениза Шмандт-Бессера сделала вывод, что счетные бирки обозначали главные товары того времени: зерно, скот, кувшины масла. К 40 в.  до  н.  э.  счетные  бирки  нанизывали  на  бечевку, как  бусы.  Но  такое  число  несложно  поменять,  добавив либо убрав «бусины», исходя из этого были введены особые меры предосторожности.  Целый  комплект  бирок  оборачивали  в глину, которую после этого  обжигали. Любой  спор о числах  возможно  было дать добро,  разбив глиняную обертку. С 35 в. до н. э., дабы не разламывать любой раз «документ», бюрократы старой Месо­потамии  начали  делать  надпись  на  «конверте»,  перечисляя содержащиеся в бирки. После этого  до  какого-либо  умника  дошло,  что  надпись  снаружи делает бирки в лишними. Результатом стало  появление совокупности письменных числовых знаков, проложивших доро­гу всем последующим совокупностям числовой нотации и, возмож­но, письменности по большому счету.